The New Sudoku Players' Forum

[champagne]

[ronk-moderator edit: title "exocet pattern" formerly known as "bi bi pattern"]

Hi,

I open this new thread to comment the way I am introducing in the solver the specific pattern found at the start of several “hardest puzzles” as

Code: Select all

100000007020400060003000500090040000000062040000900800005000003060200080700001000 Silver Plate   
000000039000001005003050800008090006070002000100400000009080050020000600400700000 GoldenNugget
000000006005001800090008070000802000003010200400503000060000090008300100700000004 tarx0075

000000003001005600090040070000009050700000008050402000080020090003500100600000000 fata morgana
.......1......4.32.2..3.5.......7....4..2...5..89..4....78..6...3..1..5.9........ coly004 #
000000002001000700030050090000006040003040800040509000090060030002000100700003000 trompel'oeil
000000007020400060100000500090002040000800600600900000005003000030080020700004001 Tungston Rod   

The pattern has been first described by Alan Barker in the first loop for Fata Morgana .

Some specific aspects have been discussed recently is several threads as
Great Monster loopshttp://forum.enjoysudoku.com/viewtopic.phpt=6407?
Almost fish patternshttp://forum.enjoysudoku.com/viewtopic.php?t=6490
AIC’s nets equivalent to forcing netshttp://forum.enjoysudoku.com/viewtopic.php?t=6444

This wants to be a summary of findings telling how the pattern can be used in the main path of a solver working on AIC’s and AIC’s nets.

I wanted a short name for that pattern. I chose “bi bi” (2 cells linked to 2 other cells). May be native English speakers can make a better proposal.

My introduction of the pattern properties will use the text I prepared on my web site for the start of the V2 version of Golden Nugget to come when this will be finalized.

For the time being, using partially that tool, my solution for Golden Nugget is better than halved.

The text below ( image format) can be captured here.

http://pagesperso-orange.fr/gpenet/UX/Sample7GN/V2_fichiers/GNV2D01.htm



champagne

[ttt]

I open this new thread to comment the way I am introducing in the solver the specific pattern found at the start of several “hardest puzzles” as

Code: Select all

100000007020400060003000500090040000000062040000900800005000003060200080700001000 Silver Plate   
000000039000001005003050800008090006070002000100400000009080050020000600400700000 GoldenNugget
000000006005001800090008070000802000003010200400503000060000090008300100700000004 tarx0075

..........

I can’t retired by you..., but thanks for that
I’m studying your solution for GN, hope to find some thing new (at least for me)…

BTW, regardless some difficult but WE ARE NEVER GAVE UP. That is LIFE, RIGHT?

ttt

[champagne]

I can’t retired by you..., but thanks for that
I’m studying your solution for GN, hope to find some thing new (at least for me)…

GN seems to be good for a player using all the power of the "bi bi".

Silver Plate does not offer the same possibilities (no elimination of super candidates). For the time being, I get nearly no improvement in Silver Plate, but I have to finish the task and to debug.

I did not check for other puzzles except Fata Morgana but you know the very good result you can get with that puzzle. That one is now solved in about 5 seconds, heavily downgraded in the ranking.

Good work and don't hezitate to call for improvements in the text file.

champagne

ps: next elimination in GN proposed by the solver is <9>r3c2. You can try to find it. Folwing steps seem tougher.

[ttt]

...and don't hezitate to call for improvements in the text file.

Yes, and to solve hardest puzzles like GN, tarx0075, SP… we (Allan, champagne, ronk, ttt …) need more people like Carcul, re’born, RW, Steve K… Don’t know they can…

ttt

[ronk]

We will show that whatever if the super candidate in the red cells, the blue cells are filled with the same 2 digits
[...]
row 7 dead row 3 dead row 3 dead row 3 dead

No possibility to have “Blue False” . At least one blue cell is occupied.

For each super candidate, the 2 blue cells are occupied by the same digits.

<3> r7c9

For which the "best fit SLG" is:

Code: Select all

14 Sets  = {1247R3 1247R4 1247R7 12N7}
18 Links = {1247b3 1247c7 27c1 14c2 12c4 47c6 4n8 7n9} ==> r7c9<>3

Very nice result!

[champagne]

For which the "best fit SLG" is:

Code: Select all

14 Sets  = {1247R3 1247R4 1247R7 12N7}
18 Links = {1247b3 1247c7 27c1 14c2 12c4 47c6 4n8 7n9} ==> r7c9<>3

Very nice result!

This SLG does exactly the same in "set mode".

For me, the most interesting points using "bi bi" is:

1) split of the difficulty in four sub problems,
2) re use of the property for elimination of super candidates and of the remaining limited number of scenarios.

point 1) can be expressed in that way: If you don't find a "bi bi" with one digit using a start, give up and look for another start.
Reversely, if you find one, try other digits for the same potential "bi bi".

point 2) is the most important to crack such a puzzle in a simple way.
I have still some work to show it, but I am now confident. Silver Plate could be an exception. Nothing exciting comes in a first shot.

Another point is that with a full scan, I did not find other "bi bi"s. Same in all puzzles in the list I gave in the first post.

Subject to "no bug", it seems that such pattern can not appear twice!!!

champagne

[ronk]

For me, the most interesting points using "bi bi" is:

1) split of the difficulty in four sub problems,
[...]
point 1) can be expressed in that way: If you don't find a "bi bi" with one digit using a start, give up and look for another start.
Reversely, if you find one, try other digits for the same potential "bi bi".

On his web (or hosting) site, Allan Barker illustrated this logic set for Golden Nugget ...



... which proves the (derived) strong inference set (SIS) ... {r2c8, r3c8, r3c9, r4c8, r7c9} = {12467}

This SIS is a distributed hidden locked set. With only five unfilled cells in b3, and with three of the SIS cells (r2c8, r3c8, r3c9) seeing r12c7, it's rather obvious that r12c7 will contain the same digits as the remaining cells of the SIS (r4c8, r7c9). It's a law-of-leftovers kind of scenario.

If the cell distribution of the derived SIS were different, you might have a mono mono, a tri tri, or a quad quad. (I'm laughing because IMO the terminology is silly.)

As to frequency of occurrence, there's likely a derived SIS for most of the "rank 1" eliminations associated with "almost SK-loops". Of course, not all will be useful.

point 2) is the most important to crack such a puzzle in a simple way.

I haven't studied your r1c7<>7 elimination path yet.

[champagne]

On his web (or hosting) site, Allan Barker illustrated this logic set for Golden Nugget ...
... which proves the (derived) strong inference set (SIS) ... {r2c8, r3c8, r3c9, r4c8, r7c9} = {12467}

This SIS is a distributed hidden locked set. With only five unfilled cells in b3, and with three of the SIS cells (r2c8, r3c8, r3c9) seeing r12c7, it's rather obvious that r12c7 will contain the same digits as the remaining cells of the SIS (r4c8, r7c9). It's a law-of-leftovers kind of scenario.

If the cell distribution of the derived SIS were different, you might have a mono mono, a tri tri, or a quad quad.

1) The SLG shown by ALLAN on his web site I studied includes floor 6. It seems to be that one.
You likely have other ways to "prove" how the SLG works, but I checked that the "bi bi" logic applies.

Anyway, I am looking specifcally for that "bi bi" pattern. The search could be extended as you say. In fact, when I apply Allan Barker model, there is no limitation in the search.

The "bi bi" pattern has proven to be efficient in several puzzles,
it is a pattern a player has a good chance to find,
it leads up to now to one "bi bi" to analyze, which is perfect for a player,
the constraints of the "bi bi" will give, as shown in that post to a very limited number of scenarios, each scenario having from the beginning a significant number of assigned.

These conditions together give good chances to crack the puzzles with a limited number of moves easy to express in AIC's nets form.

I had a look at the situation at the end of my web page.

As I wrote, it easy to establish <9>r3c1 at that point, but, unless I made a mistake, you can easily reduce as well the number of authorized scenarios from 4 to 3 (elimination of 1&7r12c7.)

I now give the priority to the final design of the process, so you or ttt should come with a nice solution before I finish the coding.

champagne

[ttt]

Hi champagne,
Very nice find and great works!

Now,I understand your concept. For eliminating r1c7=7, it look like “ floor + ” :
- If r1c7=1 => r1c7<>7
- If r1c7<>1 => floor (247)r12c7 and the same as FM => pair (24)r12c7 => r1c7<>7 - on using URs at r12c37 & r12c57

I now give the priority to the final design of the process, so you or ttt should come with a nice solution before I finish the coding.

Waiting for me some days…

Edit:

next elimination in GN proposed by the solver is <9>r3c2. You can try to find it. Folwing steps seem tougher.

I found :
1- If r3c2=1 => r3c2<>9
2- If r3c2<>1 => floor (247)r12c7 => pair (24)r12c7 => to avoid UR(24)r12c37 at least [(4)r5c3, (2)r6c3] must be true => r3c2<>9 but quite complex…

ttt

[champagne]

Now,I understand your concept. For eliminating r1c7=7, it look like “ floor + ” :
- If r1c7=1 => r1c7<>7
- If r1c7<>1 => floor (247)r12c7 and the same as FM => pair (24)r12c7 => r1c7<>7 - on using URs at r12c37 & r12c57

Nothing wrong, but I would stress on the logic followed by the solver.

1) r12c7 is an AC2 having six possible supercandidates 1&2 1&4 1&7 2&4 2&7 4&7
2) each of the digit patterns in that AC2 lead to a unitary "bi bi" with r4c8 r7c9
so we have a full "bi bi" r12c7; r4c8;r7c9
3) No room for other digits in r4c8 r7c9 (no role later)
4) Each super candidate fill r4c8;r7c9 with the same digits.
analysing each bi-floors linked to supercandidates, it appears that
2&7;4&7 are not valid
(you try to do it in once, here it is searched in 2 independant steps)

5) we are left with still valid for r12c7 1&2 1&4 1&7 2&4
The last possibility for digit '7' is 1&7 => <7>rc7.


That sequence is stricly what the solver can find.
This is a reason why I stay cautious towards the fact that the solver can not find more in Silver Plate.
Opening the scope, it can be that a player can do more with the "bi bi" existing in that puzzle.

next elimination in GN proposed by the solver is <9>r3c2. You can try to find it. Folwing steps seem tougher.

I found :
1- If r3c2=1 => r3c2<>9
2- If r3c2<>1 => floor (247)r12c7 => pair (24)r12c7 => to avoid UR(24)r12c37 at least [(4)r5c3, (2)r6c3] must be true => r3c2<>9 but quite complex…

ttt

Again, let me tell why it seems to me that the "bi bi" view can make it relatively simple.
We have to keep in mind the findings made before and my assumprion is that, having a unique "bi bi", it is acceptable to study it in detail to ease the search.

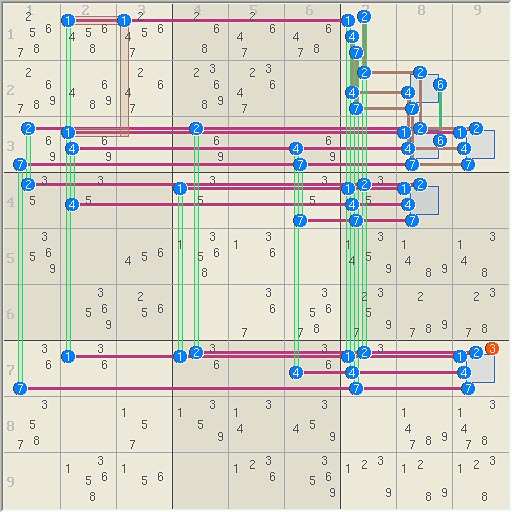
Code: Select all

25678   14568  1K24567 |268      2467   4678b  |1i24   3      9     1&7 1&2 1&4 2&4
26789   4689   2467    |23a68Â9Ä 23A467 1      |247    246c7  5     
2679    1i469  3       |269      5      4679Æ  |8      1246C7 1247 
-------------------------------------------------------------------
2d35    34e5   8       |1j35     9      357x   |123457 1247   6     
3569f   7      4E56    |13568b   1L36   2      |13459  1489   1348 
1       3569F  2D56    |4        367À   35678B |23579  2789   2378 
-------------------------------------------------------------------
367y    136    9       |12h36    8      34p6   |12347  5      1247 
3578g   2      157z    |135s9Æ   134q   345Ì9Í |6      14789Å 13478
4       13568G 156     |7        12H36  35r69Å |1239Ç  1289   1238 

first of all, 9r3c2 - (1r3c2;1r1c7)
we have only one super candidate still valid in r1c7, so we must have 24r13c7.

I pick up the work done to check whether 2&4r13c7 coud be eliminated.

Code: Select all

Last super candidate 2&4
  digit 2       digit 4     
... .X. X..  ..X ... X..    || ..X ... X..  ... .X. X..
... .X. X..  ..X ... X..    || ..X ... X..  ... .X. X..
X.. ... ...  ... ..X ...    || ... X.. ...  .X. ... ...

... ... .X.  .X. ... ...    || X.. ... ...  ... ... .X.
... ..o ...  ... ... .X.    || ... ..o ...  ..X ... ...
..X ... ...  ... o.. ...    || ... ... .X.  ... o.. ...

... X.. ...  ... ... ..X    || ... ... ..X  ... ..X ...
.o. ... ...  ... .X. ...    || .o. ... ...  ... ... ..X
... ... ..X  o.. ... ...    || ... .X. ...  o.. ... ...

The right scenario has 4r3c2 which is not possible,
So we are sure that we have the left scenario and we rely on that
To go further in the simplest way, I don't hesitate to insert the left scenario in the map(basic cleaning not done and small pieces of original tagging kept)

Code: Select all

25678  14568 124567 |268    2467   4678  |24     3      9     1&7 1&2 1&4 2&4
26789  4689  2467   |23a689 23A467 1     |24     246c7  5     
2      1i469 3      |269    5      4     |8      1246C7 1247 
------------------------------------------------------------
2d35   4e    8      |1j35   9      357   |123457 2      6     
3569   7     4E56   |13568  136    2     |13459  4      1348 
1      3569  2D     |4      367    35678 |23579  2789   2378 
-----------------------------------------------------------
367    136   9      |2h     8      346   |12347  5      4   
3578   2     157    |1359   4      3459  |6      14789  13478
4      13568 156    |7      12H36  35r69 |1239   1289   2   

and now the complementary pieces of AIC's

#[]9r3c2=>2r1c5 []2r9c5.H - 9r3c2
[]2r2c5 - 3r2c5 = 3r2c4 - 9r2c4 = 9r3c46 - 9r3c2
#[]9r3c2=>2r2c7 trivial after 2r1c5

#[]9r3c2 => 7r2c1 AC:r2c124
[]2r2124 - 2r2c7 <=9r3c2
[]4r2c2 - 4r4c2 <=9r3c2
[}6r2c124 - 6r2c8 <=6r3c4 <=9r3c2

#[]9r3c2=>7r6c5
[]7r1c5 - 2r1c5 <= 9r3c2
[]7r2c5 - 3r2c5 <= 9r3c2

and with our simplified map

clear []9r3c2 => 7r2c1 - 7r7c1 = 7r7c7 - 7r4c7 = 7r4c6 - 7r6c5 <= 9r3c2


No problem to put all that in AIC's net.

champagne

[ttt]

Hi champagne,
For GN, I found next move based on “bi bi” pattern (1247)[r12c7, r4c8, r7c9] is r2c4<>2…

And other is r9c2<>1 with considering (1567)r89c3 & “bi bi” pattern (1247)[r12c7, r4c8, r7c9]:
1- Pairs [(15), (16), (17)]r89c3 => r9c2<>1
2- Pair (67)r89c3 => r7c2=1 => r9c2<>1
3- Pair (56)r89c3 after some simple steps (considering 7’s on col.7) => r7c7=7 => r7c2=1 => r9c2<>1
4- Pair (57)r89c3 => r1c3=1 => r1c7<>1 => floor (247)r12c7 => pair (24)r12c7 and “bi bi” pattern => (24)[r4c8 & r7c9] and not too difficult to find r7c2=1 => r9c2<>1
I’m not sure for presenting it nice on AIC’s net and finding more deductions require more time…

ttt

[champagne]

Hi champagne,
For GN, I found next move. . . r2c4<>2…

And other is r9c2<>1 . . .

I’m not sure for presenting it nice on AIC’s net and finding more deductions require more time…

ttt

With an imperfect view of the "bi bi", my solver found after <9>r3c2

#3r7c4
#7r2c1
#7r7c9
#1r5c4
#1r8c4
#1r9c2 . . .

your second move is there, not the first.

One important point is that this is done nearly at level 3 in the solver compared to a long preliminary path at level4 in the former version.

I hope that with a complete view of the "bi bi" pattern the path will really turn to something short.

Showing for example <1&7> r12c7 at the very beginning would be a huge step, killing 7r2c7 and ipso facto 7r4c8;r7c9. I hope something like that will come.

Regarding the AIC's net expression, I am not sure it has a big added value compared to the sequence of derived weak links I am printing.

For sure, a new way to express the "bi bi" pattern in an equivalent AIC form must be agreed upon.

It could be somethng like

Code: Select all

    |~a | = . . .
X - | & |
    |~b | = . . .

X super candidate
a,b the 2 linked candidates in the second part of the "bi bi"
~a expressing the binary logical complement. Could be also (!a) &(!b)



I personnaly feel comfortable inserting the scenario in the map of candidates.

champagne

[Allan Barker]

Champagne, and ttt,

Very nice logical work I guess the French traslation of bi-bi must be ... au revoir - au revoir
What is interesting is how many more eliminations you can find for Golden Nugget

1) The SLG shown by ALLAN on his web site I studied includes floor 6. It seems to be that one.
You likely have other ways to "prove" how the SLG works, but I checked that the "bi bi" logic applies.

This one is an early elimination that used floor 6. A morphed version in the
GN Morph and tarx0075 Comparision uses only the 1,2, 4, and 7 stories. When morphed back to the oringinal GN configuration, it becomes this:

For which the "best fit SLG" is:

Code: Select all

14 Sets  = {1247R3 1247R4 1247R7 12N7}
18 Links = {1247b3 1247c7 27c1 14c2 12c4 47c6 4n8 7n9} ==> r7c9<>3

which looks like it follows the same logic:

[champagne]

This one is an early elimination that used floor 6. A morphed version in the
GN Morph and tarx0075 Comparision uses only the 1,2, 4, and 7 stories. When morphed back to the oringinal GN configuration, it becomes this:

For which the "best fit SLG" is:

Code: Select all

14 Sets  = {1247R3 1247R4 1247R7 12N7}
18 Links = {1247b3 1247c7 27c1 14c2 12c4 47c6 4n8 7n9} ==> r7c9<>3

I did not study in detail that version but I knew it existed.

In fact, the way I find these "bi bi" pattern is a simplified version of your permutation algorithm. Consequently, the SLG must exist.

Champagne, and ttt,

Very nice logical work I guess the French traslation of bi-bi must be ... au revoir - au revoir
What is interesting is how many more eliminations you can find for Golden Nugget

Let me disagree with the first part of your sentence.

I learned a lot thru your SLG model and I am implementing several "heretic" uses of it. The way I find the "double XWing deadly pattern" is strictly a hidden use of your logic.


I already expressed my feeling about the weakness of the "restricted SLG approach" if I can say so.

1) all the findings here are relying on your first loop properties. The problem is that in your SLG model, that property appears only with a base of about 40 sets. No chance to find others eliminations based on that properties with a small SLG.

2) I am adding a deadly pattern logic, what is not authorized in your model. This is very important.

To be honest, in the way I code that process, I make the bet that the constrainst of the "bi bi" pattern lead to some situations easy to establish. I would feel more confortable if had a kind of SLG proof at the end.



My feeling is that you can do very well, may be in a complementary way if you find a process re using the findings of a first step in the next ones. Ths is exactly what i did.

I just run a file of "hardest puzzles", the "bi bi" pattern is in a wide majority of them, (you can see it in the new "hardest puzzle thread"), so you should concentrate on that specific pattern as well.


BTW, I proposed "bi bi" because it can be used indiferently in English and in French.

I hope to continue to see you here with your own view of that pattern


champagne

[ronk]

I proposed "bi bi" because it can be used indiferently in English and in French.

Most search engines discard two-letter words. For that reason alone, "bi bi" is an unwise choice.