The New Sudoku Players' Forum

[ronk]

Present as diagram:
Diagram 1: Floor (357)r6c56 => r6c238<>7

You keep coming up with gems using a presentation style that's fairly easy to understand. In this case, however, r6c238<>7 seems to depend upon the elimination r6c5<>1. Where is that proven?

[ttt]

Present as diagram:
Diagram 1: Floor (357)r6c56 => r6c238<>7

You keep coming up with gems using a presentation style that's fairly easy to understand. In this case, however, r6c238<>7 seems to depend upon the elimination r6c5<>1. Where is that proven?

Thanks and I meant, to eliminate r6c5=3:
1- If r6c5=1 => r6c5<>3
2- If r6c5<>1 => Floor (357)r6c56 => two sub-steps (diagram 1: r6c238<>7) & (diagram 2: r6c1289<>5) => pair (57)r6c56 (we can use this as pattern for other eliminations?) => r6c5<>3

Conclude: r6c5<>3

ttt

[Allan Barker]

Hi all,

Working with ttt's AUR idea, I found the same eliminations in a couple of different ways: The first one below is a composite of ttt's logic

Composite summary of ttt's r6c5<>3 elimination. (Note the uncovered 1r6c5).

15 Sets = {3R28 7R28 3C248 5C248 7C248 6N56}
19 Links = {3r169 5r169 7r6 7c56 5n2 19n4 4n8 3b357 5b5 7b19}
2 AURs = [ (37)r26c56 + (37)r68c56 ]
1 Elimiantion r6c5<>3,

A slightly smaller design using a different structure.

13 Sets = {7R28 3C258 5C248 7C28 6N6 3B28}
17 Links = {3r169 5r169 7r6 3c6 7c56 5n2 19n4 4n8 5b5 7b19}
2 AURs = [ (37)r26c56 + (37)r68c56 ]
1 Elimiantion r6c5<>3,

A design that does not use floors, but uses two "walls" in c28.

18 Sets = {3R28 7R28 3C45 5C4 13679N2 6N6 13679N8}
29 Links = {3r169 5r169 7r6 134578c2 7c5 37c6 123579c8 19n4 3b37 5b5 7b19}
2 AURs = [ (37)r26c56 + (37)r68c56 ]
1 Elimiantion r6c5<>3,

If there are floors and walls, then logically the AURs are the windows?

Ttt, again nice work. My program is showing most eliminations need 2 AURs, but I was not sure this is correct. Your logic suggests this is correct.

Thumbs.


Walls.

[ttt]

A slightly smaller design using a different structure.
13 Sets = {7R28 3C258 5C248 7C28 6N6 3B28}
17 Links = {3r169 5r169 7r6 3c6 7c56 5n2 19n4 4n8 5b5 7b19}
2 AURs = [ (37)r26c56 + (37)r68c56 ]
1 Elimiantion r6c5<>3

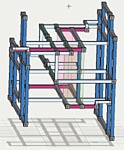
It looks better, I’ll study to how can present it as AIC’s net

If there are floors and walls, then logically the AURs are the windows?

Yes, and more: sometimes the AURs are… the doors

My program is showing most eliminations need 2 AURs

Yes, it’s a reason that SP is champagne’s special puzzle

BTW, I’m studying your eliminations for PB (17 elims) to understand your concepts and hope some useful for me.

ttt

[champagne]

Hi champagne,
I don’t know below deduction on your list for SP or not: r6c5<>3

Code: Select all

Silver Plate
1.......7.2.4...6...3...5...9..4........62.4....9..8....5.....3.6.2...8.7....1...
 
 *-----------------------------------------------------------------------------*
 | 1       4(5)8   4689    |(35)68   23589   35689   | 2349    2(3)9   7       |
 | 589     2      (7)89    | 4      (357)189(357)89  | 1(3)9   6       189     |
 | 4689    4(7)8   3       | 16(7)8  12789   6789    | 5       129     12489   |
 |-------------------------+-------------------------+-------------------------|
 | 23568   9       12678   | 1(357)8 4       3578    | 12367   12(357) 1256    |
 | 358     1(357)8 178     | 1(357)8 6       2       | 1379    4       159     |
 | 23456   14(357) 12467   | 9      [1](357)(357)    | 8       12(357) 1256    |
 |-------------------------+-------------------------+-------------------------|
 | 2489    148     5       | 6(7)8   789     46789   | 124679  12(7)9  3       |
 |(3)49    6       149     | 2      (357)9  (3457)9  | 14(7)9  8       1459    |
 | 7      (3)48    2489    |(35)68   3589    1       | 2469    2(5)9   24569   |
 *-----------------------------------------------------------------------------*

. . .
ttt

For the time being, my solver just finds direct effect of the EXOCET r5c56 r4c8 r5c2 giving <2>r4c8 <8>r5c2.

I have a lot to do and no time to finish full implementation of flying fishes effect. I will come in due time with fresh comments.

To show I am not inactive, I found recently the smallest Exocet.

This is a puzzle from coloin not yet published on that forum.

Code: Select all

...4....87.......9..3.9.5....9.6...51....23...7....6....6.8..5......1....2...4...#coly510

Seen by my solver, it is in the family of hardest. It has one cell with only 2 candidates.

If you take it as a base, you'll find an Exocet with specific properties.

Using these properties, the puzzle collapse.

but may be you'll find it easy without Exocet

[ronk]

As nobody reacted, I take flying fish for an elementary "bi bi" and EXOCET for the full "bi bi"

I don't known how it sounds in Englsh, but exocet is the French name for a flying fish and it has been taken 20 years ago as name for a flying torpedo.

Sigh. It seems to me that the basic words that describe this concept are "equivalence" and "pairs". Although "bi bi" didn't communicate equivalence, at least it communicated the idea of pairs. "Flying fish" and "exocet" communicate neither.

BTW what is the difference between "elementary bi bi" and "full bi bi"

[champagne]

As nobody reacted, I take flying fish for an elementary "bi bi" and EXOCET for the full "bi bi"

I don't known how it sounds in Englsh, but exocet is the French name for a flying fish and it has been taken 20 years ago as name for a flying torpedo.

What is the difference between "elementary bi bi" and "full bi bi"

The primary component for a "full bi bi"=Exocet is

One "group" of digits such as
if that group is true
then at least one of 2 other cells would be filled with the same digit.

To have a full "bi bi"=Exocet,

if you take a base having several digits (eg 123 123)
each group of one digit must have the "elementary property" in association with the same 2 cells.

base one cell 2 digits:
full "bi bi" if both candidates have an elementary "bi bi" with the same cells (last example)

base 2 cells 3 digits as in Fata Morgana
full "bi bi" =Exocet if each of the 3 groups has an elementary "bi bi" with the same 2 cells.

base 2 cells 4 digits as in Golden Nugget change 3 in 4 in the previous sentence.

any AC2 (n cells n+2 digits n-2 digits compulsory) works exactly in the same way as with 2 cells 4 digits.

Between a flying fish=elementary"bi bi" and the Exocet = "full bi bi", you have an intermediate situation. Each time 2 digits have the matching elementary "bi bi" as described above, most of the property of the full "bi bi" are already available (at least if the base is solved by super candidates (2 digits), which is the case for AC2 and "123 123" patterns).

As we have seen in Platinium Blonde, other patterns using elementary "bi bi" = "flying fish" exist.

champagne

[ronk]

What is the difference between "elementary bi bi" and "full bi bi"

The primary component for a "full bi bi"=Exocet is

One "group" of digits such as
if that group is true
then at least one of 2 other cells would be filled with the same digit.

I don't see the "elementary" term in that, but is this supposed to be the definition for "elementary bi bi"?

Whether or not it is, if only "one of 2 other cells would be filled with the same digit", would this "primary component" be useful?

[ttt]

This is a puzzle from coloin not yet published on that forum.

Code: Select all

...4....87.......9..3.9.5....9.6...51....23...7....6....6.8..5......1....2...4...#coly510

Seen by my solver, it is in the family of hardest. It has one cell with only 2 candidates.
If you take it as a base, you'll find an Exocet with specific properties.
Using these properties, the puzzle collapse.

but may be you'll find it easy without Exocet

I found two BBs:
1- BB r12c7 r4c8 r7c9 => r4c8<>8, r7c9<>3
2- BB r56c9 r3c8 r7c7 => r3c8<>6, r7c7<>9
After above the puzzle has not collapsed yet… , I’ll study more…

BTW, I like to call BB instead of Exocet. Suggestion : CART
Edit 1&2: combinate two BBs => r4c7 & r3c9<>1247 and the puzzle collapse. Right?

ttt

[champagne]

This is a puzzle from coloin not yet published on that forum.

Code: Select all

...4....87.......9..3.9.5....9.6...51....23...7....6....6.8..5......1....2...4...#coly510

I found two BBs:
1- BB r12c7 r4c8 r7c9 => r4c8<>8, r7c9<>3
2- BB r56c9 r3c8 r7c7 => r3c8<>6, r7c7<>9
After above the puzzle has not collapsed yet… , I’ll study more…

BTW, I like to call BB instead of Exocet. Suggestion : CART
Edit 1&2: combinate two BBs => r4c7 & r3c9<>1247 and the puzzle collapse. Right?

ttt

Hi ttt,

In coly510, the solver did not enter analysis of AC2. The puzzle was cracked before.

Due to the downgraded form 123 123 in r5c59, he tried to find a BB on that base.
In that search, he got.

4r5c9 => r3c8 r7c7 flying fish
7r5c9 => r3c8 r7c7 flying fish


This is the simplest BB/Exocet form.

The effect is specific due to the strong link in r5c9.

What is sure is that with a very poor handling of that pattern, the solver could do a lot.
If you extract the best of it, you should come to a very simple path.

Full use of the pattern include for example specific weak links as

126r3c8 - 129r7c7

champagne

[ronk]

This is a puzzle from coloin not yet published on that forum.

Code: Select all

...4....87.......9..3.9.5....9.6...51....23...7....6....6.8..5......1....2...4...#coly510

A morph with maximal symmetry is ...

Code: Select all

 . . . | . . . | . . 4
 . . 6 | . 8 . | 9 . .
 . 2 . | 1 . 4 | . . .
-------+-------+-------
 . . 5 | . . . | . 9 8
 . . . | . 5 . | . . .
 6 3 . | . . . | 5 . .
-------+-------+-------
 . 1 . | . . . | . 7 .
 . . 9 | . 6 . | 3 . .
 7 . . | . . 2 | . . .  # coly510 morphed to p-4 symmetry

p-4 means ... except for 4 clues, pi (180-degree) rotational symmetry. The original is p-13.

[ttt]

....9..5..1.....3...23..7....45...7.8.....2.......64...9..1.....8..6......54....7 coly013,coloin 1.4 BB r12c7 r4c9 r8c3 BB r56c8 r3c9 r9c7

Code: Select all

 *-----------------------------------------------------------------------------*
 | 367     3467    3678    | 12678   9       12478   |[168]    5       12468   |
 | 5679    1       6789    | 2678    24578   2478    |[689]    3       24689   |
 | 569     456     2       | 3       458     148     | 7       14689  (1689)4  |
 |-------------------------+-------------------------+-------------------------|
 | 12369   236     4       | 5       238     12389   | 13689   7      [1689]3  |
 | 8       3567    13679   | 179     347     13479   | 2      (169)    13569   |
 | 123579  2357    1379    | 12789   2378    6       | 4      (189)    13589   |
 |-------------------------+-------------------------+-------------------------|
 | 23467   9       367     | 278     1       23578   | 3568    2468    3468    |
 | 12347   8       137     | 279     6       23579   | 1359    1249    1349    |
 | 1236    236     5       | 4       238     2389    |(1689)3 [1689]2  7       |
 *-----------------------------------------------------------------------------*

Perhaps typo, I found: BB r12c7 r4c9 r9c8 BB r56c8 r3c9 r9c7. This puzzle is similar to coly 510.
The combination two BBs above => r4c7 & r3c8<>1689 and the puzzle becomes trivial…

ttt

[champagne]

[quote="ttt]Perhaps typo, I found: BB r12c7 r4c9 r9c8 BB r56c8 r3c9 r9c7. This puzzle is similar to coly 510.
The combination two BBs above => r4c7 & r3c8<>1689 and the puzzle becomes trivial…

ttt[/quote]

Hi "ttt" you have the good one.

I restart work to morrow, but I see you become more and more efficient.

champagne

[champagne]

Hi,

Things are going slowly, but it goes on.
The solver can now process Fata Morgana is an appropriate way. Still some work on Golden Nugget.

The full solution will come here

http://pagesperso-orange.fr/gpenet/UX/Sample8FM/FM00.htm

For the time being, just the start here below. detailed comments can be accessed thru the web page.





champagne

[ronk]

Third group is a small list of other situations as example SK + BB

1.......2.2.....6...34..5.....8.5.....8.3.9.....9.4.....5..34...7.....1.6.......7 dukdiamond1,coloin 3.2 SK *bb(2)r5c1289 r3c6 r7c4

I find the SK-loop and BB r46c5 r3c6 r7c4. What does r5c1289 have to do with it?