The New Sudoku Players' Forum

[Wecoc]

This started as a silly joke but ended with a quite interesting puzzle.

Each colored row must contain 1-9 (including the white one). Each 3x3 grid and each column must contain 1-9 (as always).
In other words: A row can have the same number twice only if each one is in a different color.

PUZZLE 1

Old: Show

Code:

Code: Select all

5.84...............7..8..9.............21..373.........4....5...6..2.......7.....

PUZZLE 2

Old: Show

Code:

Code: Select all

.....3..9.1.........................5....2.4...2.7............1.....86...9..1....

If you drink, don't sudoku!

[creint]

Both have multiple solutions.

Try

Code: Select all

5.84...............7..8..9.............21..373.........4...95...6..2.......7....2

Code: Select all

.....3..9.18.............7..........5....2.4...2.7............1.....86...9..17...

[Wecoc]

Thank you for testing this, I tend to get something terribly wrong in my examples, probably because I create them in a spritesheet like a madman (I know what you're thinking, alcohol had nothing to do with this)
That's why I made an algorithm to test it for me... and you were absolutely right
From now I'm using this so no more silly mistakes should happen anymore. I'm curious, did you try it by hand or with some coding?

I'll show what I got in each case.

Code: Select all

PUZZLE 1 Solution (creint fix)
+-----------------------+
| 5 9 8 | 4 9 1 | 4 5 1 |
| 1 3 4 | 6 5 7 | 8 2 6 |
| 6 7 2 | 3 8 2 | 7 9 3 |
+-----------------------+
| 7 1 9 | 9 6 5 | 1 4 5 |
| 4 8 5 | 2 1 4 | 9 3 7 |
| 3 2 6 | 8 7 3 | 2 6 8 |
+-----------------------+
| 2 4 3 | 5 4 9 | 5 1 9 |
| 9 6 1 | 1 2 8 | 3 7 4 |
| 8 5 7 | 7 3 6 | 6 8 2 |
+-----------------------+

PUZZLE 2 Solution (creint fix)
+-----------------------+
| 6 4 3 | 9 4 3 | 8 6 9 |
| 9 1 8 | 7 6 5 | 3 2 4 |
| 2 5 7 | 2 8 1 | 1 7 5 |
+-----------------------+
| 3 6 9 | 4 5 9 | 7 3 6 |
| 5 8 4 | 1 3 2 | 9 4 2 |
| 1 7 2 | 8 7 6 | 5 1 8 |
+-----------------------+
| 7 3 6 | 6 9 4 | 4 9 1 |
| 4 2 1 | 3 2 8 | 6 5 3 |
| 8 9 5 | 5 1 7 | 2 8 7 |
+-----------------------+

I made new ones, this time properly validated. I hope you liked the idea for the variant

PUZZLE 3

Code: Select all

1.....4...3.632.91...........5.7...66...4........................3.9.12..8...5...

PUZZLE 4

Code: Select all

..8...9.....1..........2..6.......13..15....8.........42.....3...9..........5....

[creint]

Solved with my solver and solved with SAT, both work of course.
I did not need to add new code, only design and input which took less than 2 minutes.
I can make a vertical variant within one minute.

[Wecoc]

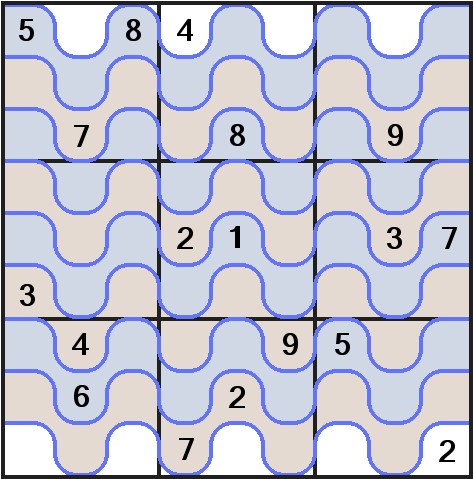
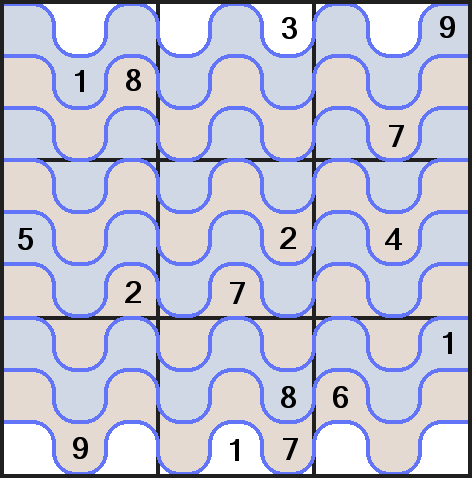
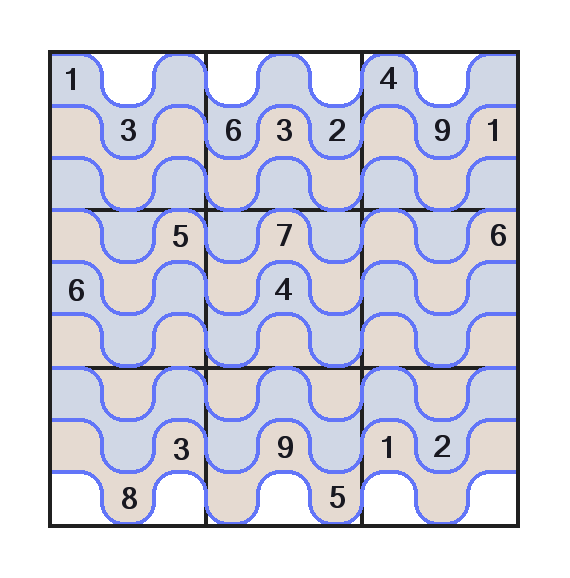
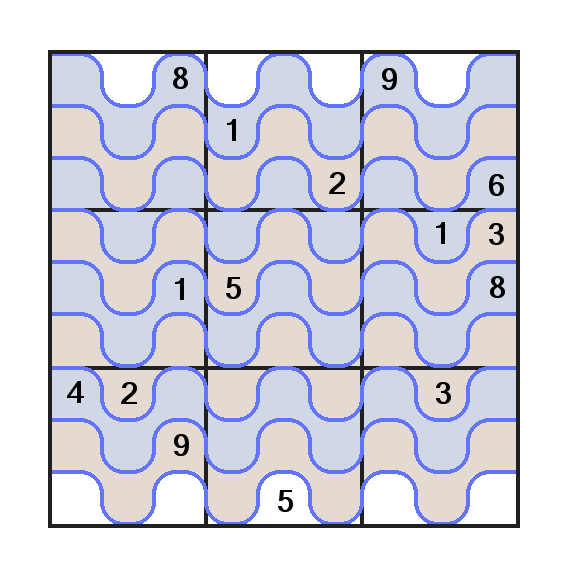
Thank you again. I don't think a vertical one would be necessary since it would be the same but rotated 90/270º.

There's something else that draws attention here, though.
First I'll explain how I made my solver.

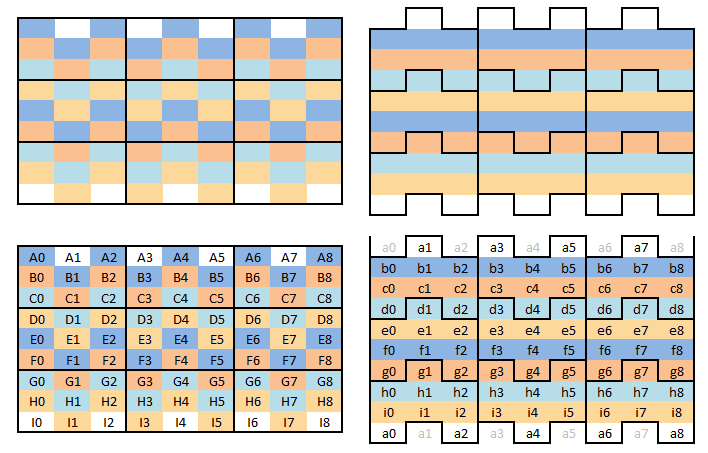
I transformed a little bit the puzzle so the rows are alined, but the boxes are the ones with strange shape instead. Everything is preserved except the display of the puzzle itself (I simply moved up the even columns), later I'll explain why.

Image: Show

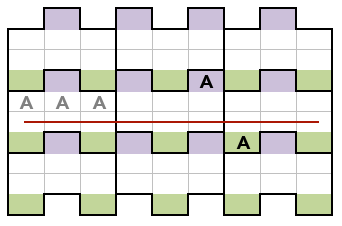
The result is a Jigsaw Sudoku, but a special one because of the white row both in top/bottom.
Note: I changed the way indexes work to fit the rows.

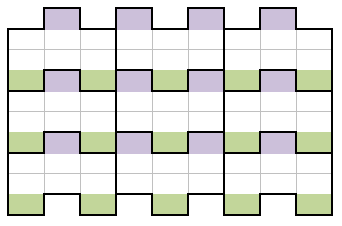
Ok, now the interesting part. As you can see there are 2 types of tabs, upper tabs (purple) and lower tabs (green).

Image: Show

That's very helpful to eliminate candidates because once a number is set to be placed in one type of tab, in the other affected rows it must be in the same type. Otherwise there would always be a row that can't contain that number, which is against sudoku rules.

Image: Show

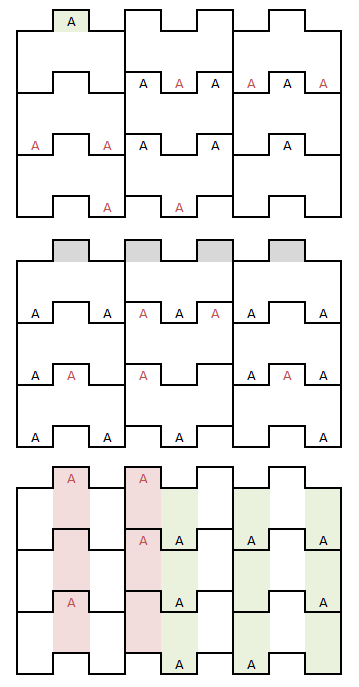
I added 3 restrictions based on this:

Image: Show

1- If a candidate is solved in any of the upper tabs, we can eliminate it as candidate in all lower tabs. Same can be applied on lower tabs.
2- If a candidate isn't found in any of the upper tabs of one row, that means the candidate must be on the lower tabs, so we can eliminate it in all other upper tabs. Same can be applied on lower tabs.
3- If a candidate can't be placed in at least 3 different columns of the 4 possible among the upper tabs it must be in the lower tabs instead. Same can be applied on lower tabs, but considering there are 5 possible columns in that case.

This is a good shortcut to eliminate candidates in early stages but sadly I haven't been able to make a solvable puzzle that isn't still solvable without this trick
It takes much longer but still reaches the correct answer, I'm not sure that would always be the case

[Wecoc]

I didn't mention this but as far as I've seen, because of the way tabs work it seems impossible to exist a Sudoku which givens are valid both in a classic sudoku and a drunk sudoku.
First it would need to be a No-touch sudoku because of the column displacement, but in that situation the tabs result in a blank cell with no available candidates.
Looks like semi-alcoholism isn't and can't be a thing after all

Puzzle 3 Solution: Show

Code: Select all

+-----------+
|158|451|437|
|432|632|591|
|769|987|682|
+-----------+
|345|573|816|
|621|149|345|
|897|268|279|
+-----------+
|514|314|953|
|273|896|124|
|986|725|768|
+-----------+

Puzzle 4 Solution: Show

Code: Select all

+-----------+
|218|364|924|
|534|175|371|
|967|982|586|
+-----------+
|642|213|413|
|371|548|298|
|895|697|657|
+-----------+
|423|421|135|
|189|739|762|
|756|856|849|
+-----------+