The New Sudoku Players' Forum

[koushanejad74]

enoku is a logic-based number-placement puzzle. It is distinct from but shares some properties and rules with Str8ts and Sudoku.
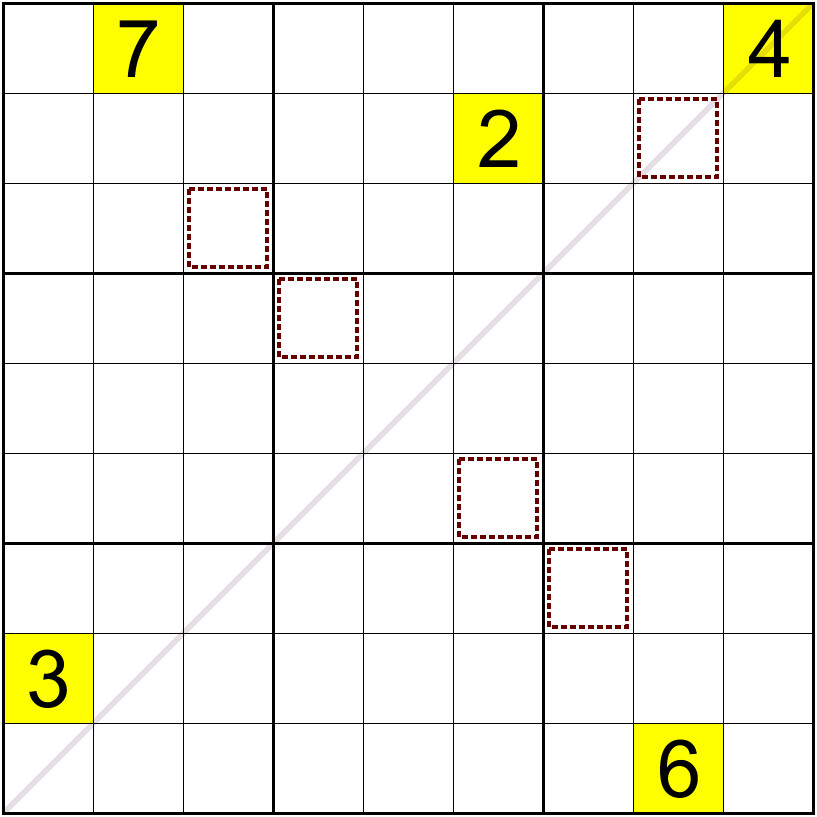
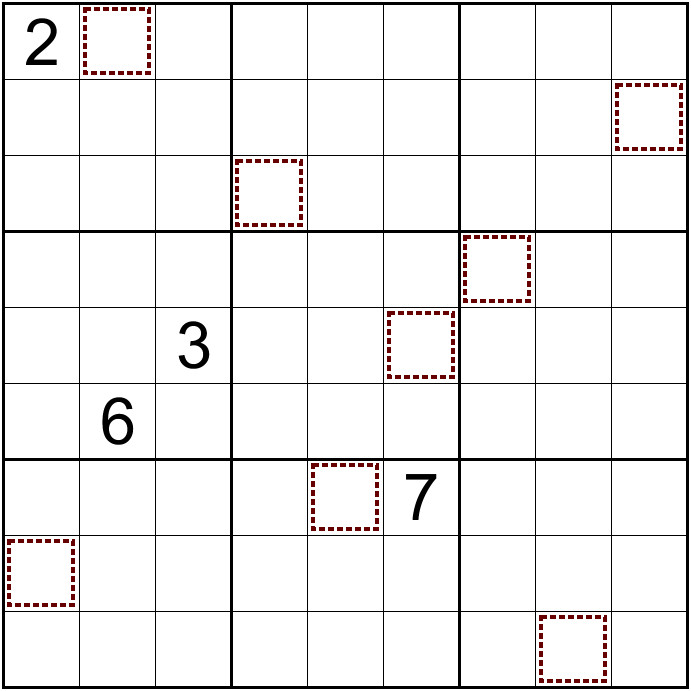
Rules:
• All sudoku rules apply.
• Some rows and columns are divided into two compartments by a gray cell
• Each compartment, vertically or horizontally, must contain a straight – a set of consecutive numbers, but in any order. For example: 7, 6, 4, 5 is valid, but 1, 3, 8, 7 is not.
• Each puzzle has a UNIQUE solution

Benoku Definition:PDF

Benoku Sample (Hard)

Gray cells are shown with [ ]

Code: Select all

 0  [0]  3   |  0   0   0   |  0   0   0 
 0   0   0   |  0   0  [0]  |  0   0   0 
 0   0   0   |  0   0   0   |  0   0   0 
----------------------------------------
[0]  0   0   |  0   0   0   |  2   0   0 
 0   0   0   | [0]  0   0   |  0   0   0 
 0   8   0   |  0   0   0   |  0   0  [0]
----------------------------------------
 0   0  [0]  |  0   0   0   |  0   0   0 
 4   0   0   |  0   0   0   | [0]  0   0 
 0   0   0   |  0   0   0   |  0   0   0 


[SCLT]

This puzzle does indeed have a unique solution:

Hidden Text: Show

Code: Select all

+---------+---------+---------+
| 8  9  3 | 7  6  2 | 1  4  5 |
| 6  4  2 | 5  3  1 | 7  8  9 |
| 7  1  5 | 8  9  4 | 3  2  6 |
+---------+---------+---------+
| 9  7  4 | 6  1  5 | 2  3  8 |
| 2  3  1 | 9  4  8 | 6  5  7 |
| 5  8  6 | 2  7  3 | 4  9  1 |
+---------+---------+---------+
| 1  2  9 | 4  8  6 | 5  7  3 |
| 4  6  8 | 3  5  7 | 9  1  2 |
| 3  5  7 | 1  2  9 | 8  6  4 |
+---------+---------+---------+


I wouldn't have called it particularly hard, though - it still solved using only simple compartment rules and basic Sudoku techniques. What process are you using to designate these puzzles as "easy" or "hard"?

[koushanejad74]

This puzzle does indeed have a unique solution:

Hidden Text: Show

Code: Select all

+---------+---------+---------+
| 8  9  3 | 7  6  2 | 1  4  5 |
| 6  4  2 | 5  3  1 | 7  8  9 |
| 7  1  5 | 8  9  4 | 3  2  6 |
+---------+---------+---------+
| 9  7  4 | 6  1  5 | 2  3  8 |
| 2  3  1 | 9  4  8 | 6  5  7 |
| 5  8  6 | 2  7  3 | 4  9  1 |
+---------+---------+---------+
| 1  2  9 | 4  8  6 | 5  7  3 |
| 4  6  8 | 3  5  7 | 9  1  2 |
| 3  5  7 | 1  2  9 | 8  6  4 |
+---------+---------+---------+


I wouldn't have called it particularly hard, though - it still solved using only simple compartment rules and basic Sudoku techniques. What process are you using to designate these puzzles as "easy" or "hard"?

That's the hard part, I have an algorithm that generates the puzzles and also solves them, the solver is not that smart and I use the number of guesses as the difficulty.
Any help would be appreciated, basically how to determine the difficulty?

[koushanejad74]

can you try this one, this is the hardest I could generate

Code: Select all

 0   0   0   |  0   0   0   | [0]  0   0 
 0   0   0   |  0   0   0   |  0   0   0 
 0   0   0   |  0  [0]  0   |  0   0   0 
----------------------------------------
 0   0   0   |  0   0   0   |  0   0   5 
 0  [0]  0   |  0   0   0   |  0   0   0 
 0   0   0   |  0   0  [0]  |  0   0   0 
----------------------------------------
[0]  0   0   |  3   0   0   |  0   0   0 
 0   0   0   |  0   0   0   |  0  [0]  0 
 0   0   0   |  0   6   0   |  3   0   0 


But as I said before, I need to work on how difficulty is calculated

[SpAce]

This puzzle does indeed have a unique solution:

Hidden Text: Show

Code: Select all

+---------+---------+---------+
| 8  9  3 | 7  6  2 | 1  4  5 |
| 6  4  2 | 5  3  1 | 7  8  9 |
| 7  1  5 | 8  9  4 | 3  2  6 |
+---------+---------+---------+
| 9  7  4 | 6  1  5 | 2  3  8 |
| 2  3  1 | 9  4  8 | 6  5  7 |
| 5  8  6 | 2  7  3 | 4  9  1 |
+---------+---------+---------+
| 1  2  9 | 4  8  6 | 5  7  3 |
| 4  6  8 | 3  5  7 | 9  1  2 |
| 3  5  7 | 1  2  9 | 8  6  4 |
+---------+---------+---------+


I wouldn't have called it particularly hard, though - it still solved using only simple compartment rules and basic Sudoku techniques.

It's hard enough for me! I guess I'm missing something obvious because I can't get very far with it. I can see how you get your solution once all black cells are solved (c4 being the key), but I can't see how to get there. If fact, I can't get any cells solved with the starting grid! This is embarrassing Can you help me out?

This is as "far" as I get:

Hidden Text: Show

Code: Select all

.----------------------.-----------------------------------.--------------------------------.
|  89   [19]     3     |  1245678    1245678     128       |  145678   1245678    1245678   |
|  678   12456   12456 |  123456789  123456789  [19]       |  134678   12346789   12346789  |
|  678   12456   12456 |  123456789  123456789   123456789 |  1345678  123456789  123456789 |
:----------------------+-----------------------------------+--------------------------------:
| [19]   145679  14567 |  1345678    1345678     1345678   |  2        1345678    1345678   |
|  123   1234    124   | [19]        456789      456789    |  45678    456789     456789    |
|  156   8       14567 |  12345679   12345679    12345679  |  134567   1345679   [19]       |
:----------------------+-----------------------------------+--------------------------------:
|  123   123    [19]   |  3456789    3456789     3456789   |  345678   345678     34678     |
|  4     3567    789   |  12356789   12356789    12356789  | [19]      12378      12378     |
|  356   3567    789   |  123456789  123456789   123456789 |  189      12345678   1234678   |
'----------------------'-----------------------------------'--------------------------------'

There are some chaining eliminations available in box 4, but they don't help. You said such techniques shouldn't be needed anyway.

[SCLT]

Hi SpAce,

To get from your position to a few solved cells, you want to look at row 8. In particular, r8c3 is at least a 7, so there cannot be a 1 in the left half of that row. Furthermore, the cells on the right cannot be 7/8 as that would leave the 9 in r8c3 stranded. So a 2 is locked into r8c89.

Then the fact that r8c9 is at most a 3 gives some more eliminations in r789c9, leaving a 3/4 naked pair and giving a few placements.

I see that you'd already noticed the locked 9s when you have a black cell one cell away from the edge of the grid and the cell on the edge is missing 2 as a candidate - that would have been the other tip I would have given you.

Maybe the puzzle is harder than I thought Nevertheless, it is, I promise, possible to solve entirely using basic logic and compartment steps similar to those I describe here

[SpAce]

To get from your position to a few solved cells, you want to look at row 8. In particular, r8c3 is at least a 7

Thanks! That was the key I'd missed. It was enough to solve the rest relatively easily.

Maybe the puzzle is harder than I thought

Well, at least it was the hardest Benoku for me thus far, being the first I couldn't solve without help Leren's Benokus required harder sudoku techniques, but the Benoku-specific parts were much more obvious so I never had any problem with them. In fact, I think this was a very good puzzle because it was all Benoku-logic and still felt non-trivial.

Btw, did you try the other one? I can't get anywhere with that either Here's where I'm stuck:

Hidden Text: Show

Code: Select all

.-----------------------------------.------------------------------.---------------------------------.
|  123456789   123456789  123456789 | 12456789   123789     123456 | [19]        123789     123789   |
|  123456789   123456789  123456789 | 12456789   123789     123456 |  12456789   123456789  12346789 |
|  123456789   123456789  123456789 | 12456789  [19]        123456 |  12456789   123456789  12346789 |
:-----------------------------------+------------------------------+---------------------------------:
|  12346789    12346789   12346789  | 1246789    1234789    12346  |  1246789    12346789   5        |
|  1289       [19]        123456789 | 12456789   12345789   123456 |  1246789    12346789   12346789 |
|  123456789   123456789  123456789 | 12456789   12345789  [16]    |  24789      234789     234789   |
:-----------------------------------+------------------------------+---------------------------------:
| [19]         12456789   12456789  | 3          1245       789    |  245678     245678     24678    |
|  123789      123456789  123456789 | 1245       1245       789    |  245678    [19]        1289     |
|  12789       1245789    1245789   | 1245       6          789    |  3          1289       2478     |
'-----------------------------------'------------------------------'---------------------------------'


I can see how some 12-combinations in r1c789, r123c5, and r8c89 can't be true together, but that doesn't help.

[HATMAN]

Hi Kousha

In your rules I believe you should explicitly state that the hidden cell has a value.

In other Renban Group puzzles it does not have one. In fact in creating a good Str8ts puzzle at least one hidden cell should have a different value in each direction to avoid being able to plug into a Sudoku solver.

I use JSudoku a lot when creating puzzles but with Renban groups it has a bug in the solver and it also assumes the hidden cell has a value.

Maurice

[Leren]

HATMAN wrote: In your rules I believe you should explicitly state that the hidden cell has a value.

Amen to that. Admittedly, if you look in the Benoku definition file above, he gives an example where a blank grey cell in the puzzle takes on a value in the solution, but it's easy to miss.

Another thing that should be stated in the rules is whether or not there can be more than one grey cell in the one box. The puzzles posted so far suggest that only one grey cell per box is the rule.

Leren

[Leren]

Well FWIW here is the unique solution to that last puzzle.

Code: Select all

473586912
251493768
689712543
368974125
197825436
542631879
916348257
834257691
725169384

But I could only solve it by putting in 5 or 6 extra clues - that's one brute of a puzzle !

Leren

[HATMAN]

Benoku D H4TM4N 1

I decided to play around with N5 given it has more possibilities.

Two blocking cells in a nonet is quite restricted. I'll try and see if 9 blocking cells can be done.

This works well in JSudoku provided that you do not use the Renban Group facility.

Solved without guesses but Udosuk would say I used too many elimination chains.

Note it is D/.

0 7 0 | 0 0 0 | 0 0 4
0 0 0 | 0 0 2 | 0 [] 0
0 0 [] | 0 0 0 | 0 0 0
-------------------------
0 0 0 | [] 0 0 | 0 0 0
0 0 0 | 0 0 0 | 0 0 0
0 0 0 | 0 0 [] | 0 0 0
-------------------------
0 0 0 | 0 0 0 | [] 0 0
3 0 0 | 0 0 0 | 0 0 0
0 0 0 | 0 0 0 | 0 6 0

[koushanejad74]

HATMAN wrote: In your rules I believe you should explicitly state that the hidden cell has a value.

Amen to that. Admittedly, if you look in the Benoku definition file above, he gives an example where a blank grey cell in the puzzle takes on a value in the solution, but it's easy to miss.

Another thing that should be stated in the rules is whether or not there can be more than one grey cell in the one box. The puzzles posted so far suggest that only one grey cell per box is the rule.

Leren

Thanks Leren & Hatman,

I'll modify the description as you suggested,
the fact that there's not more than one gray cell in each box, is not a rule, but it's intentional. since the gray cells, in most cases, can only take 1 or 9, having two of them in one box will it easy

[HATMAN]

Benoku 8 block H4TM4N 2

I have managed this one with 8 blocks. given I started with a four cell symmetry and did not use two blocks in a nonet I think 9 blocks is possible but will need number crunching. Does anyone want to try?

On difficulty: the structure does not make difficulty it is the puzzle maker's choice. This one with one block to a nonet is easy, my previous one had two blocks in one nonet and was hard.

Apologies Leren is correct I made a mistake on my assumptions for r1c1, r1c9, r9c1, r9c9. I had r1c1=2 if you wish to do the puzzle - corrected now.

I will look at it again to see if there is a ninth block with this formulation.

2 [] 0 | 0 0 0 | 0 0 0
0 0 0 | 0 0 0 | 0 0 []
0 0 0 | [] 0 0 | 0 0 0
-------------------------
0 0 0 | 0 0 0 | [] 0 0
0 0 3 | 0 0 [] | 0 0 0
0 6 0 | 0 0 0 | 0 0 0
-------------------------
0 0 0 | 0 [] 7 | 0 0 0
[] 0 0 | 0 0 0 | 0 0 0
0 0 0 | 0 0 0 | 0 [] 0

[Leren]

My Benuko solution counter says your puzzle has 119 solutions. You can make it unique by adding one more clue eg r1c1 = 2 does the trick. The solution is not difficult.

I'm assuming this is a vanilla Benoku and not the diagonal constrained one you posted above. Here is the solution with r1c1 = 2 on the left and a solution with r1c1 = 1 on the right.

Code: Select all

219753468   194752368
354861279   325864179
687942351   687931245
598674123   548673921
143529687   213549687
762138945   769128453
425317896   452317896
971286534   971286534
836495712   836495712

Leren