(First published on www.mathpuzzle.com this week)

It is standard sudoku with one more condition: the same numbers are not "knight move connected".

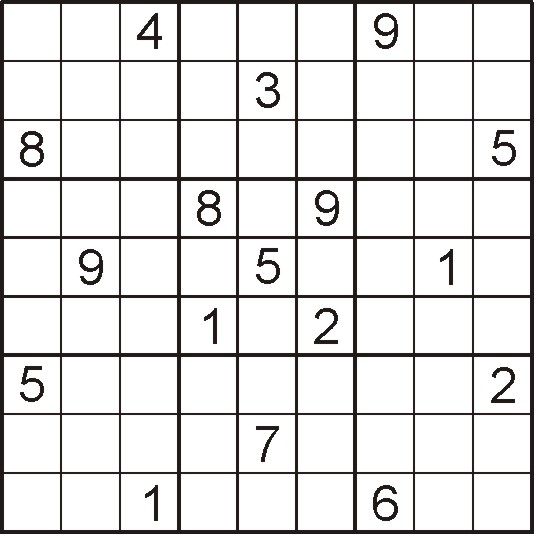
MichalStajszczak wrote:It has very curious feature, which one can see examining numbers in this diagram, but is valid for all numbers in the solution
That feature was discussed
Formal definition of gurth's symmetrical placement wrote:Let the 9 values be a1,a2,b1,b2,c1,c2,d1,d2,e.
In the initial setup of a puzzle, if each of r[i]c[j] and r[10-i]c[10-j] are {a1,a2} or {b1,b2} or {c1,c2} or {d1,d2} or {e,e} or both empty, and r5c5 is {e} or empty,
then all other cells must all have this property.
MichalStajszczak wrote:The next step is sudoku anti-knight and diagonal:
....
MichalStajszczak wrote:I have prepared a new (I hope) variant of sudoku: "anti-knight sudoku". ....
....
Smythe Dakota wrote:Clarification, please.
If by "diagonal" you mean ANY diagonal, not just the longest diagonals (r1c1-r9c9 and r1c9-r9c1) then there is no solution, as there is no cell in the upper middle box where a 9 can go.
Or maybe you intended to outlaw only diagonally ADJACENT same digits.
Yes, exactly the same feature I'm talking about...
udosuk wrote:.... No, it's just no repetition on the 2 main (longest) diagonals ....