- Code: Select all
top1465 #488
9..51...35..3..2....8..2...7.....5.8.96...31....8...9.3.5.7.6.....1.........3..85
After SSTS:
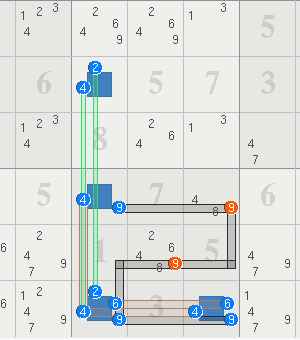
9 2467 247 | 5 1 46 | 8 467 3
5 1467 147 | 3 4689 4689 | 2 467 1469
146 3 8 | 7 469 2 | 149 5 1469
-------------------+--------------------+------------------
7 124 1234 | B2469 469-2 13 | 5 246 8
8 9 6 |BA24 5 7 | 3 1 24
124 5 1234 | 8 A246 13 | 47 9 2467
-------------------+--------------------+------------------
3 148 5 | B49 7 89 | 6 24 1249
246 24678 2479 | 1 24689 5 | 479 3 479
1246 12467 12479 | 2469 3 469 | 1479 8 5
Sets: A = {r5c4, r6c5} = {246}; B = {r457c4} = {2469}; x,z = 6,2
Elim: r4c5<>2
NL: r4c5 -2- als:[r5c4,r6c5] -6- als:r457c4 -2- r4c5 ==> r4c5<>2
Note that the overlap cell r5c4 does not contain the restricted-common-candidate (RCC) <6>
- Code: Select all
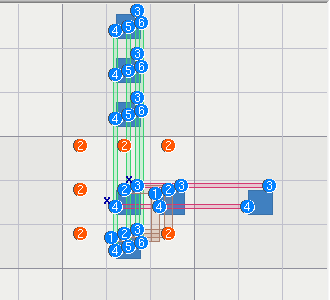
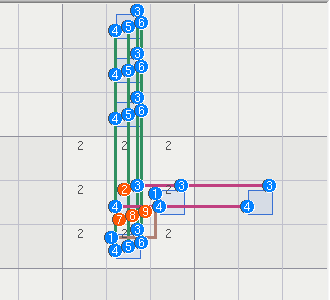
9 2467 247 | 5 1 46 | 8 467 3
5 1467 147 | 3 4689 4689 | 2 467 1469
146 3 8 | 7 469 2 | 149 5 1469
-------------------+---------------------+------------------
7 124 1234 | 2469 2469 13 | 5 246 8
8 9 6 | B24 5 7 | 3 1 24
124 5 1234 | 8 246 13 | 47 9 2467
-------------------+---------------------+------------------
3 148 5 |BA49 7 48-9 | 6 24 1249
246 24678 2479 | 1 2468-9 5 | 479 3 479
1246 12467 12479 | B2469 3 A469 | 1479 8 5
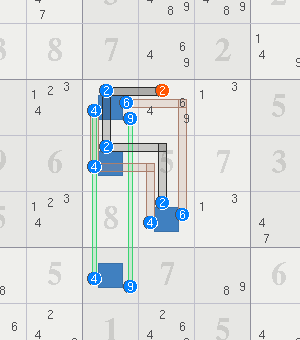
Sets: A = {r7c4,r9c6} = {469}; B = {r579c4} = {2469}; x,z = 6,9
Elim: r7c6<>9, r8c5<>9
NL: [r7c6,r8c5] -9- als:[r7c4,r9c6] -6- als:r579c4 -9- [r7c6,r8c5] ==> r7c6<>9, r8c5<>9
As above, note the overlap cell r7c4 does not contain the RCC
1) [edit: Excluding notational preferences, are] there simpler ways to obtain or view these eliminations?
2) The above structures have box and line (row, column) base sets that intersect. Are there examples from real puzzles with an intersecting row and column as well?
[edit: As noted by Luke451 & aran, r8c5<>9 added to 2nd example]

 .............
.............