The New Sudoku Players' Forum

[ronk]

I run into 2-set ALS Chains with overlap occasionally. Here's a more recent one from UK Extreme #141, but with the added wrinkle of an rc thru a conjugate link (overlap cell: r8c6):
Green set (23457) r8c456/r9c4 -> rc=2 via 2-conjugate r2c46 -> Blue set (1247) r158c6 => r9c6<>7

Hmm, you could use locked candidates (2)r2\\b2 ==> r1c46<>2
and then naked pair (47)r18c6 ==> r29c6<>7, r5c6<>4

[DonM]

Hmm, you could use locked candidates (2)r2\\b2 ==> r1c46<>2
and then naked pair (47)r18c6 ==> r29c6<>7, r5c6<>4

That's all you can say about my pretty overlapping 2-set example- which was apparently the subject of the thread?

[ronk]

Hmm, you could use locked candidates (2)r2\\b2 ==> r1c46<>2
and then naked pair (47)r18c6 ==> r29c6<>7, r5c6<>4

That's all you can say about my pretty overlapping 2-set example- which was apparently the subject of the thread?

It's a very pretty graphic.

[PIsaacson]

Don,

My ALS engine identified a Death Blossom with the same conjugate stem cells r2c46 {2}, but a single ALS petal r18c6 {247} linked to both sides of the conjugate stem. So, the ALSs are a 100% complete overlap from this POV. These were the 5th through 7th steps out of 93 DBs found from the initial PM.

Code: Select all

  5) r5c6 <> 4 db[2] t2 stem-cells r2c4 r2c6 2 ALS[1] 2-r18c6 ALS[2] 2-r18c6
  6) r2c6 <> 7 db[2] t2 stem-cells r2c4 r2c6 2 ALS[1] 2-r18c6 ALS[2] 2-r18c6
  7) r9c6 <> 7 db[2] t2 stem-cells r2c4 r2c6 2 ALS[1] 2-r18c6 ALS[2] 2-r18c6

This DB recapitulates the two step claiming pair/naked pair sequence as described by Ron.

[Allan Barker]

My ALS engine identified a Death Blossom with the same conjugate stem cells r2c46 {2}, but a single ALS petal r18c6 {247} linked to both sides of the conjugate stem. So, the ALSs are a 100% complete overlap from this POV. These were the 5th through 7th steps out of 93 DBs found from the initial PM.

Code: Select all

  5) r5c6 <> 4 db[2] t2 stem-cells r2c4 r2c6 2 ALS[1] 2-r18c6 ALS[2] 2-r18c6
  6) r2c6 <> 7 db[2] t2 stem-cells r2c4 r2c6 2 ALS[1] 2-r18c6 ALS[2] 2-r18c6
  7) r9c6 <> 7 db[2] t2 stem-cells r2c4 r2c6 2 ALS[1] 2-r18c6 ALS[2] 2-r18c6

This DB recapitulates the two step claiming pair/naked pair sequence as described by Ron.

Combining AHS + ALS is a very interesting subject.
However in this case, the recapitulation may be little more that a short lived strategic pullback.

My mini solver found the same but used only 3 covers{47c6 2b2}for the three thuths in {2R2 18N6}, (i.e., r1c6, r8c6, and the bi-local row set 2r2c45). This renders the logic as rank 0 and, in AHS/ASL terms, may be closer to a Sue de Coq or a doubly linked continuous loop. In this case, digit 2 seeing itself through column 6 is always redundant.

Code: Select all

DONX: 7 Candidates, Rank = 0
      3 Base (truths) = {2R2 18N6}, 3 Covers = {47c6 2b2}
      5 Eliminations --> 
(1N6*2b2) => r1c6<>2,    //cannibal
(2b2) => r1c4<>2 
(7c6) => r29c6<>7 
(4c6) => r5c6<>4

Since the only way to get this elimination requires that box 2b2 fully cover the bi-local in row 2, this logic must always contain a smaller, embedded locked candidates move.

Of course, this just shows there are many ways to view ALS et.al., and DonM's 2 set overlap example remains a pretty as ever.

BTW:Finding this with the mini solver requires v93 or above, which has a new "Get Cannibal" button.
.

[DonM]

Don,

My ALS engine identified a Death Blossom with the same conjugate stem cells r2c46 {2}, but a single ALS petal r18c6 {247} linked to both sides of the conjugate stem. So, the ALSs are a 100% complete overlap from this POV. These were the 5th through 7th steps out of 93 DBs found from the initial PM.

Code: Select all

  5) r5c6 <> 4 db[2] t2 stem-cells r2c4 r2c6 2 ALS[1] 2-r18c6 ALS[2] 2-r18c6
  6) r2c6 <> 7 db[2] t2 stem-cells r2c4 r2c6 2 ALS[1] 2-r18c6 ALS[2] 2-r18c6
  7) r9c6 <> 7 db[2] t2 stem-cells r2c4 r2c6 2 ALS[1] 2-r18c6 ALS[2] 2-r18c6

This DB recapitulates the two step claiming pair/naked pair sequence as described by Ron.

Hi Paul and Allan! Extreme #141 really did offer up a virtual cornucopia of ALS Chain patterns. Man I love solving in this way as a change from the usual AIC chains. As I've said before, it's not that's it's better, it's that it's different enough that it increases the fun/interest aspect and introduces a new challenge which is why I do any of this at all. Not that many weeks ago, I never would have believed that some of these Extreme puzzles could be manually solved with nothing but ALS Chains (and basic methods as necessary of course).

With that in mind, I want to thank both of you for your contributions and interest in the ALS Chain related area. If it weren't for Paul and his work, I likely wouldn't have been inspired to look into the manual advanced ALS Chain possibilities in the first place and Allan's interest (& compliments which mean a lot ) in the area has also given me new ideas. Also, Allan's graphics program is ingenious. If I weren't already well set up with a suite of programs for my graphics, I would definitely be using it more often. Both your contributions are to me the ideal in the melding of the world of computer & manual solving much in the way of the legacy from people like Rubylips, Mike Barker, Ruud and a few others.

My apologies to ronk for going a bit off topic, but to bring things back to (well almost anyway) to the topic, here's an interesting overlapping 3-set ALS Chains from Extreme #141. (Maybe something like it was in your results Paul.)



Green set(236)r29c4-> rc=3 -> Blue set(2378)r9c78/r7c9-> rc=7 thru dual 7-conjugate -> Yellow set(2678)r2c456) => r1c45<>6, r3c5<>6 (Overlap cell: r2c4)

[ronk]

My apologies to ronk for going a bit off topic, but to bring things back to (well almost anyway) to the topic, here's an interesting overlapping 3-set ALS Chains from Extreme #141.



Green set(236)r29c4-> rc=3 -> Blue set(2378)r9c78/r7c9-> rc=7 thru dual 7-conjugate -> Yellow set(2678)r2c456) => r1c45<>6, r3c5<>6 (Overlap cell: r2c4)

This is a much much improved example, but let's be clear. It's a chain with 3 ALSs, not a "3-set ALS Chain". To be precise, there are 5 sets, 3 ALSs and 2 AHSs, so appropriate names might be ... 5-set ALS/AHS chain ... or 3-ALS/2-AHS chain.

[ronk]

Here is a ALS-xy -- aka 3-set ALS chain -- with endset overlap. As it has no conjugate links, it is a true 3-set ALS chain.

Note that three cells of the endsets overlap. There are, therefore, three different 'z' candidates for potential eliminations.

Code: Select all

 
top1465 #920 except c4/c5 swapped
...2...48...6.4.1...4..73......52471....7...92.7.4.........3....8....5...69.....3
 
After SSTS
+---------------------+-------------------------+---------------------+
| 135679  13579  1356 |  2        139   B(159)  | 679     4      8    |
| 35789   23579  2358 |  6        389    4      | 279     1      257  |
| 15689   1259   4    | C(1589)   189    7      | 3       2569   256  |
+---------------------+-------------------------+---------------------+
| 3689    39     368  |AC(389)    5      2      | 4       7      1    |
| 13458   1345   1358 |AC(138)    7     B(168)  | 268     23568  9    |
| 2       1359   7    |AC(1389)   4     B(1689) | 68      3568   56   |
+---------------------+-------------------------+---------------------+
| 1457    12457  125  |  4578-19  12689  3      | 126789  2689   2467 |
| 1347    8      123  |  47-19    1269  B(19)   | 5       269    2467 |
| 1457    6      9    |  4578-1   128    158    | 1278    28     3    |
+---------------------+-------------------------+---------------------+
 
Sets: A = {r456c4} = {1389}; B = {r1568c6} = {15689}; C = {r3456c4} = {13589}
      x, y = 8, 5; z = any of 1, 3, or 9
 
Elims: r789c4<>1, r78c4<>9 (actual)
 
NL: r789c4 -139- als:r456c4 -8- als:r1568c6 -5- als:r3456c4 -139- r789c4
    ==> r789c4<>139 (potential)

Set C (yellow) includes all three cells of set A (red).

[edit: add set marks to pencilmarks; add missing "als:" to nice loop]

[DonM]

This is a much much improved example, but let's be clear. It's a chain with 3 ALSs, not a "3-set ALS Chain". To be precise, there are 5 sets, 3 ALSs and 2 AHSs, so appropriate names might be ... 5-set ALS/AHS chain ... or 3-ALS/2-AHS chain.

To each his own. I understand that from the point of view of mathematical set theory, what you say his true. On the other hand, while some may be determined to look on Sudoku as an exercise in set theory application and choose to be anal about terminology, I see Sudoku as what it is- a puzzle game to be solved. IMO, part of the reason that higher level solving is relegated to a relative few is because of the cloaking of what are really simple concepts with terminology that few people relate to. The term, two-sector disjoint subsets, and whether the addition of a bivalue cell that doesn't see all the other cells to an ALS is a variation of an ALS or an almost disjoint subset means nothing to the layman solver, nor should it.

I'm not suggesting that all vestiges of mathematical terminology be thrown out or that there shouldn't be some care used in what patterns are classified as. On the other hand, I consider much of this as nitpicking when compared to the value of the examples being presented, especially considering that they were the result of hard-core solving.

In this case, anyone understanding the visual patterns that are in the graphic above will see why I call it a 3 set ALS Chain. There is no conceivable reason when it comes to learning how to solve using ALS Chains for a person to have to see it as 5 sets unless they also have an interest in the underlying mathematical theory. And again, IMO, they are better off seeing the conjugate links as the simple connections that they are so as not to detract from the simplicity of the overall pattern. I am more interested in people understanding the minimum of mathematical overlay necessary and the maximum of the practical application of solving methods.

[ronk]

This is a much much improved example, but let's be clear. It's a chain with 3 ALSs, not a "3-set ALS Chain". To be precise, there are 5 sets, 3 ALSs and 2 AHSs, so appropriate names might be ... 5-set ALS/AHS chain ... or 3-ALS/2-AHS chain.

I understand that from the point of view of mathematical set theory, what you say his true. On the other hand, while some may be determined to look on Sudoku as an exercise in set theory application and choose to be anal about terminology ...

OK, I'll be more direct. On this thread, an ALS chain means a chain comprised of all ALSs. If that doesn't suit you, you can take your combo ALS/AHS chains elsewhere.

And anal? I know expressions like that are why people love you so much, but do you always have to take things to a personal level?

[DonM]

This is a much much improved example, but let's be clear. It's a chain with 3 ALSs, not a "3-set ALS Chain". To be precise, there are 5 sets, 3 ALSs and 2 AHSs, so appropriate names might be ... 5-set ALS/AHS chain ... or 3-ALS/2-AHS chain.

I understand that from the point of view of mathematical set theory, what you say his true. On the other hand, while some may be determined to look on Sudoku as an exercise in set theory application and choose to be anal about terminology ...

OK, I'll be more direct. On this thread, an ALS chain means a chain comprised of all ALSs. If that doesn't suit you, you can take your combo ALS/AHS chains elsewhere.

And anal? I know expressions like that are why people love you so much, but do you always have to take things to a personal level?

If you took 'anal' in the context in which I used it as being personal then I apologize. However, being personal could also be applied to someone whose main response to a given individual's efforts is to criticize. Take a look at the first respondent to both of the ALS tutorials just as one example of umpteen. Your sandbox is all yours- you don't need to show me the way out, I can still see David's footsteps.

[Allan Barker]

Hi Paul and Allan! ........... your contributions are to me the ideal in the melding of the world of computer & manual solving much in the way of the legacy from people like Rubylips, Mike Barker, Ruud and a few others.

Don, Very well put. I have always viewed the computer as a tool to help us see, learn, and understand, which is why Xsudo is primarily logic editing and visualizing tool, rather than simply solving puzzles.

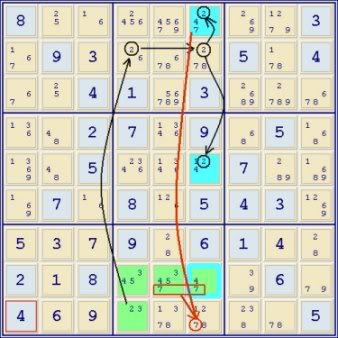
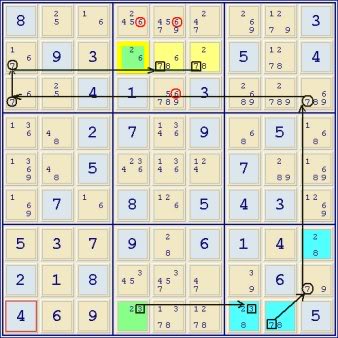
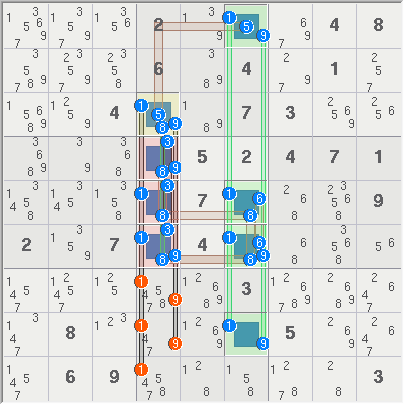
Anyway, here is another example that seems to fit the same rules, and also looks very similar to the one just posted by RonK (Seems I wasted too much time making the 3D image). The way I see this example working is:

A = als(46789)r2567c5
B = als(479)b5a48 a.k.a. als(479){r5c4,r6c5}
overlap is r6c5
X=4
Z=7

In a normal ALS-XZ rule, the Z overlaps in some region outside the ALS (i.e., some candidates see all occurrences of the Z digit).

In this case, the Z overlaps inside the ALS (i.e. some ALS candidates can see all occurrences of Z). This lowers the rank of and extended region of the ALS causing eliminations of all digits 8 and 9, instead of 7.

Code: Select all

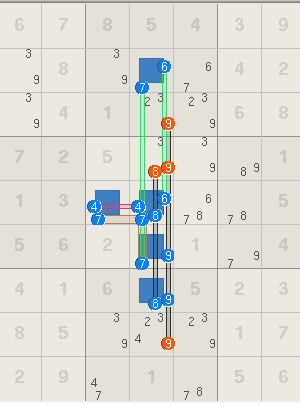
267854391108000425504100687472500016913000052856201043741605230685000170329010560
+----------+-------------------+-----------+
| 2  6   7 | 8     5       4   | 3   9  1  |
| 1  39  8 | 39    (67)    67  | 4   2  5  |
| 5  39  4 | 1     23-9    239 | 6   8  7  |
+----------+-------------------+-----------+
| 4  7   2 | 5     3-89    39  | 89  1  6  |
| 9  1   3 | (47)  (4678)  678 | 78  5  2  |
| 8  5   6 | 2     (79)    1   | 79  4  3  |
+----------+-------------------+-----------+
| 7  4   1 | 6     (89)    5   | 2   3  89 |
| 6  8   5 | 39    234-9   239 | 1   7  49 |
| 3  2   9 | 47    1       78  | 5   6  48 |
+----------+-------------------+-----------+

Left, 2D Rank 0 sets shaded black.
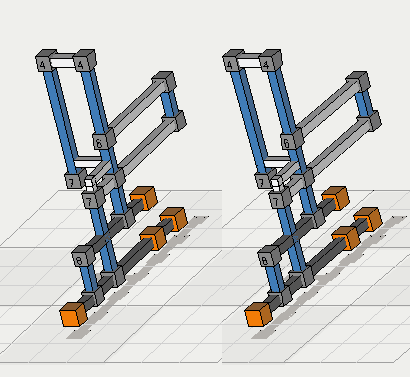
Right, 3D Stereo Hold an A4(8.5x11) page longwise between screen and nose to seperate left and right images, focus until you see a single image.
...
.
Edit: Swapped ZX to make ALS-XZ

[aran]

Code: Select all

 
top1465 #920 except c4/c5 swapped
...2...48...6.4.1...4..73......52471....7...92.7.4.........3....8....5...69.....3
 
After SSTS
+---------------------+------------------------+---------------------+
| 135679  13579  1356 | 2        139    (159)  | 679     4      8    |
| 35789   23579  2358 | 6        389    4      | 279     1      257  |
| 15689   1259   4    | (1589)   189    7      | 3       2569   256  |
+---------------------+------------------------+---------------------+
| 3689    39     368  | (389)    5      2      | 4       7      1    |
| 13458   1345   1358 | (138)    7      (168)  | 268     23568  9    |
| 2       1359   7    | (1389)   4      (1689) | 68      3568   56   |
+---------------------+------------------------+---------------------+
| 1457    12457  125  | 4578-19  12689  3      | 126789  2689   2467 |
| 1347    8      123  | 47-19    1269   (19)   | 5       269    2467 |
| 1457    6      9    | 4578-1   128    158    | 1278    28     3    |
+---------------------+------------------------+---------------------+
 
Sets: A = {r456c4} = {1389}; B = {r1568c6} = {15689}; C = {r3456c4} = {13589}
      x, y = 8, 5; z = any of 1, 3, or 9
 
Elims: r789c4<>1, r78c4<>9 (actual)
 
NL: r789c4 -139- als:r456c4 -8- als:r1568c6 -5- r3456c4 -139- r789c4
    ==> r789c4<>139 (potential)

Or one could think of that as Almost Dual-Linked ALS with
Set 1 = C above {r3456c4} = {13985}
Set 2 = B above {r1568c6} = {58169}
Almost Candidate (AlCa) : 8r3c4.

Without AlCa : dual links 5,8
Elimination potential : r789c4<>139 r9c6 <1>
With AlCa
Elimination potential : r789c4<>139
Hence elimination potential : r789c4 <139>

[aran]

PS
original example could also be looked as Almost Dual-Linked ALSs :

Code: Select all

 
 9     2467  247   |  5     1      46    | 8     467   3
 5     1467  147   |  3     4689   4689  | 2     467   1469
 146   3     8     |  7     469    2     | 149   5     1469
-------------------+---------------------+------------------
 7     124   1234  |  2469  2469   13    | 5     246   8
 8     9     6     | B24    5      7     | 3     1     24
 124   5     1234  |  8     246    13    | 47    9     2467
-------------------+---------------------+------------------
 3     148   5     |BA49    7      48-9  | 6     24    1249
 246   24678 2479  |  1     2468-9 5     | 479   3     479
 1246  12467 12479 | B2469  3     A469   | 1479  8     5
 
Sets: A = {r7c4,r9c6} = {469}; B = {r579c4} = {2469}; x,z = 6,9
Elim: r7c6<>9, r8c5<>9
 
NL: [r7c6,r8c5] -9- als:[r7c4,r9c6] -6- als:r579c4 -9- [r7c6,r8c5] ==> r7c6<>9, r8c5<>9

Set 1=r7c4+r9c6 {649}
Set 2=r459c4 {4926}
Almost Candidates (AlCas) : 4r45c4 9r4c4.

Without AlCas : dual links 4,9
eliminations <9>r8c5 <9> r7c6 etc.
With AlCa 4r45c4=>9r7c4 : =><9>r8c5 <9> r7c6
With AlCa (9-6)r4c4
=>4r7c4+6r9c6=>9r9c6 : =><9>r8c5 <9> r7c6
Hence <9>r8c5 <9> r7c6

[JasonLion-Admin]

Thanks to surbier for supplying a backup of this topic. The posts above were originally made between June 25 2009 and July 2 2009.