This is substantial rewrite of a tutorial that was presented in the Eureka forum in July, 2007 by sirdave though it was to some extent a collaborative effort between the two of us. This tutorial has a direct application in what I call type A pattern-solving ie. pure visual pattern solving, but the concepts below can also be applied for use in type B pattern-solving (ie. the nice loop and AIC chains). For instance, those familiar with nice loops or AICs will immediately notice that some of the examples could be expressed as xy-chains or grouped nice loops/AICs.
Much of this tutorial has an application for newer solvers as well as more advanced solvers so some of the descriptions that follow will be taking that into account. However, in making the information accessible to less experienced solvers some of the descriptions will, by necessity, seem rather elementary to more experienced solvers. It is assumed that the reader understands what an ALS (almost locked set) is. The basic ALS (which provides the building blocks of ALS Chains) is a group of N cells in a single house (ie. row, column or box) with candidates for N+1 digit values. Removal of one of the digit values will result in a locked set (such as a naked pair or naked triple). In addition to the examples below, newer solvers might want to check out the excellent descriptions of the ALS XZ-rule at these sites:
http://www.sudocue.net/guide.php#ALS
http://www.sudopedia.org/wiki/ALS-XZ
First a short recap: ALS patterns were first placed on the map in an organized way by bennys in the ‘Almost Locked Sets (for now)’ thread on the Player’s forum back in December, 2005 ( http://forum.enjoysudoku.com/viewtopic.php?p=16334). Since then, ALSs have been generally described as fitting into 3 general categories: the ALS XZ-rule, ALS XY-wing and ALS XY-chains. In addition, Doubly-Linked ALSs have been described, but have received much less attention than the 3 main categories. There have been a number of ALS-related threads, but none have appeared to shed much light on how to use ALSs in a practical manner that is accessible to the average solver. On the contrary, the descriptions, except for the ALS XZ-rule and one other exception, have been somewhat obscure such that it’s not surprising that the power of ALSs has often not been taken advantage of in type A pattern-solving use. The other exception is a series of Eureka threads by Anne Morelot in May and June, 2006 who provided what were the first, if not the only, examples-in-graphics of virtually all forms of the ALS patterns mentioned above. Unfortunately, a change in that forum’s software has removed the graphics so a reference to that thread would not be of much use.
There are several reasons for this tutorial. First, it is to simplify the concept of the various ALS patterns from that of what is originally three, the ALS XZ-rule, ALS X-wing and ALS XY-chains to that of one: ALS Chains. There is no real good reason to distinguish between the three categories and keeping the separate names unnecessarily complicates and confuses the situation. After all, other than the number of individual ALSs (or sets) involved, they all have the same construct: A chain of ALSs whereby, if each is connected by a ‘restricted common’ digit, then if the flanking ALSs of the chain each has the same digit, each of which ‘sees’ a common digit, then that common digit can be eliminated.
Second, is to provide graphic-based examples of the use of ALS Chains and Doubly-Linked ALSs in type A pattern-solving. Doubly-Linked ALSs are not exactly the same as ALS Chains, but they do have a close similarity to a 2-set ALS Chain and thus, can be considered a subset of ALS Chains. Finally, is to show the potential power of this solving method to those who might have been unaware of it. The fact is that it can be used to solve some puzzles above the difficulty range or most newspaper puzzles (ie. such as the diabolicals). Many advanced solvers know about ALSs and use them occasionally in type A pattern-solving and probably more often in chains, but since there have been no in-depth, clear descriptions of their use, newer solvers may be less aware of them.
Above the concept of digits 'seeing' other digits was mentioned: This usually means that all the digits are in the same house or unit ie. the same row, column or box. However, digits can also 'see' each other if they are linked by what are called conjugate pairs as will be described in more detail later.
So, on to the examples. Initially, the traditional names of what have been classed as separate categories of ALSs will be given, but further on the patterns will be named based on the concept of ALS Chains. All of the examples use the same format. The first ALS (or set) in the chain is Green, the second Blue, and if present, the third Orange and the fourth Pink. The CEC (candidate elimination cell or cell in which the elimination occurs) will be coloured Yellow. Blue arrows denote the ‘restricted common’ links between ALSs, while Red arrows denote the line of site of the flanking ALSs to the digit or candidate for elimination.
2-Set ALS Chain (aka ALS XZ-Rule)
All ALS Chains are similarly constructed. Each ALS must be connected to the next ALS in the chain by what is known as a ‘restricted common’, a digit that cannot exist at the same time in both ALSs (ie. one of them will be lost as the puzzle is solved, thus exposing the underlying locked set). Because of this bond between the ALSs, any digit (other than the restricted common) that occurs in both flanking ALSs and that is in a cell that is in the ‘line-of-sight’ (same row, column or box) of that same digit in both ALSs can be eliminated. The 2-set ALS Chain (aka ALS xz-rule) is, of course, the simplest form of ALS Chain. In the one above, the Green ALS (or set as it is sometimes called) connects to the Blue ALS via the restricted common=9, but both ALSs also contain a digit 3 that ‘sees’ the 3 in the yellow cell so it can be eliminated. Note that it is always the ‘flanking’ ALSs (ie. the ALSs at each end of the chain) that must have the common digit that ‘sees’ the candidate for elimination. When this 2-set ALS Chain was first described the ‘restricted common’ digit was arbitrarily assigned the letter (or variable) ‘x’, while the candidate for elimination was given the letter ‘z’ hence the name XZ-rule.
3-Set ALS Chain (aka ALS XY-Wing Rule)
In this 3-Set ALS Chain, the Green ALS connects to the Blue ALS via the restricted common=2. Note that there are two 2s in the Blue ALS, so be warned that when there are more than one digit equalling the digit value of the restricted common in one or more of the connecting ALSs, all of the restricted common digits of one ALS must see all the restricted common digits in the other just as the 2 in the Green ALS above sees both 2s in the Blue ALS. The Blue ALS connects to the Orange ALS via the digit 6 (the single Blue 6 seeing both of the 2 Orange 6s). Now that the 3 ALSs are thus connected, the flanking Green and Orange ALSs ‘see’ a common digit 3 in the yellow cell, so it can be removed. You can see the obvious similarity to the 2-set ALS Chain. The only difference is that an extra set has been added. ALS Chains with greater than 2 sets or ALSs will have more than one restricted common (just as the above example has the two restricted commons, 2 and 6). Therefore, it is important to note that when searching out the components of ALS Chains of greater than 2 sets, the restricted commons in the chain must have different values for adjacent sets ie. a restricted common digit value can't be the same as that of the immediately preceding or immediately following restricted common in the chain. (Please see credits at the end of the tutorial regarding this rule.)
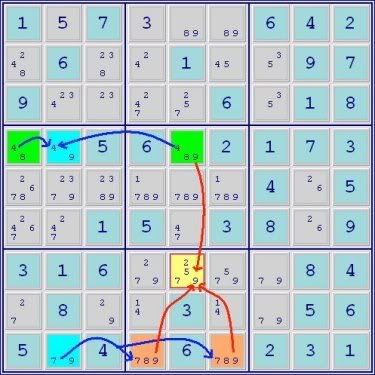
This is another example of a 3-set ALS Chain. The Green ALS connects to the Blue via the restricted common 4. The Blue ALS connects to the Orange ALS by the restricted common 7. The flanking Green and Orange ALSs converge on the 9 in the yellow cell so that it can be eliminated.
ALS Chains Greater Than 3 Sets (aka ALS XY-Chain)
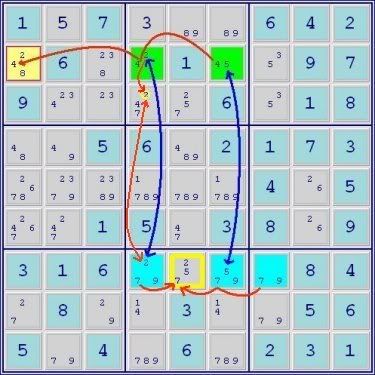
Above is a 4-set ALS Chain. The Green, Blue, Orange and now Pink, ALSs are connected by the restricted commons, 4, 7, and 9, respectively and the flanking Green and Pink ALSs see the common digit 5 for elimination in the yellow cell. Note that 5 cannot be used as a restricted common linking the Green and Blue ALSs because all the 5s in the Green set do not see all the 5s in the Blue set.
Doubly-Linked ALSs
Doubly-linked ALSs are not chains in quite the same sense as those described above are, but they might be considered a form of the 2-Set chain and therefore a subset of ALS Chains in general.
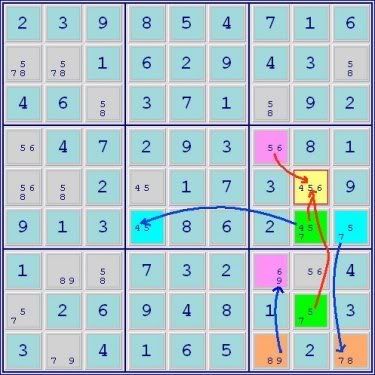
Above is an example of Doubly-Linked ALSs. They are well-known to the most advanced Sudoku solvers, but again, perhaps due to the lack of accessible descriptions of them, they are unknown to less experienced solvers. This is unfortunate because they are especially powerful in that they have as many as four different avenues of eliminations. Doubly-Linked ALSs are so-called because they are linked by two restricted commons (though some people prefer to look on these as an interchangeable restricted common and common digit for elimination).
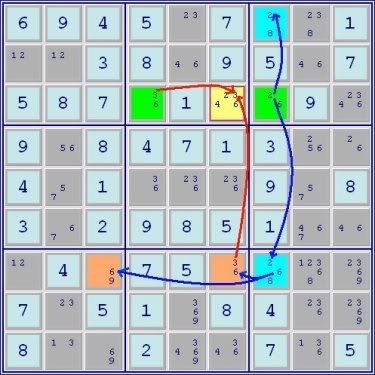
Two of the four possible sources of eliminations in Doubly-Linked ALSs (one for each ALS) derive from the fact that, if two ALSs are linked by two restricted commons, then any digits in cells (outside either ALS of course) that ‘see’ digits in either ALS that are not members of the restricted commons can be removed. In the above puzzle, the Green and Blue ALSs are linked by the restricted commons, 2 and 5. Therefore, since the 4 in the Green ALS sees the 4 in the yellow cell and is not one of the restricted commons, the 4 in the yellow cell can be removed. Likewise, by the same mechanism (but now using the Blue ALS), the 7 in the yellow-bordered cell can be removed.
The graphic also shows that the 2 in r3c4 can also be removed, but that is due to the principle that accounts for the other two means of eliminations which we'll get to in a moment.
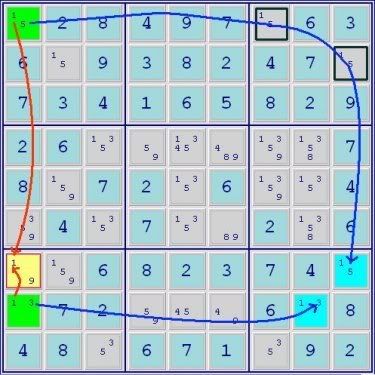
The above puzzle introduces the concept of the use of the strong links of conjugate pairs to increase the reach and thus, the power of ALS Chains and Doubly-Linked ALSs. As was hinted at earlier, all that is necessary is that the solver understand that digits in cells connected by conjugate pair links ‘see’ each other just the same as if they were in the same row, column or box. These conjugate pair links allow both the connection of sets in a chain that are remote from each other and the elimination of digits in cells that are relatively far from one or more of the flanking ALSs. In the above puzzle image, the Green and Blue ALSs are doubly-linked by the restricted commons, 3 and 5, the latter through the conjugate pair indicated by the black-bordered cells. Therefore, the remaining, non-restricted common digit 1 in the Green ALS sees and thus, eliminates the 1 in the yellow cell.
Above, it was mentioned that Doubly-Linked ALSs had four potential sources of eliminations and an example of the first two was given. The third and fourth sources derive from the fact that any digit in a cell outside each ALS, but which sees a given restricted common in both ALSs can be removed. Since this situation can occur with both of the two restricted commons, you thus have the two addition sources of eliminations. Recall that in the first example of Double-Linked ALSs, the 2 in r3c4 was eliminated by this mechanism because it sees the restricted common 2s in r2c4 and r7c4.
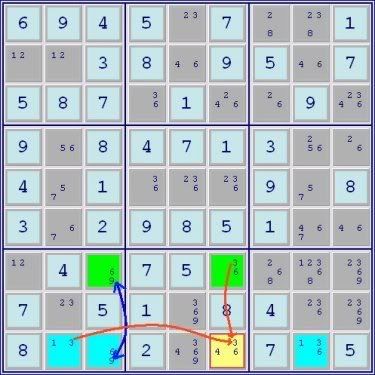
The Doubly-Linked ALS example above consists of the Green Set A: (2,4,6) r38c1 and the Blue Set B: (4,6,7,9) r348c8. They are joined by the restricted commons, 4 and 6 as indicated by the blue lines. Looking at it from the point of view of the four possible avenues of eliminations, here is a summary of the possibilities:
1. Digits that 'see' the same digits in Set A, but which are not one of the restricted commons can be removed from cells outside of Set A, in this case: r2c1<>2
2. Digits that 'see' the same digits in Set B, but which are not one of the restricted commons can be removed from cells outside of Set B, in this case: r2c8<>7 and r9c8<>9
3. Digits that 'see' the first restricted common in both Sets can be removed from cells outside of both Sets, in this case there are no 6s in row 3 that can be removed.
4. Digits that 'see' the second restricted common in both Sets can be removed from cells outside of both Sets, in this case r8c3<>4 and r8c9<>4
Thus, this one pattern results in 5 eliminations! (Note: The above example replaces an example that was defective. It is the same example that is presented in a post further along in this thread. Since some posts refer to that particular post, I decided to not delete it even though it is largely reproduced above.)
Actual Puzzle Solution Example:
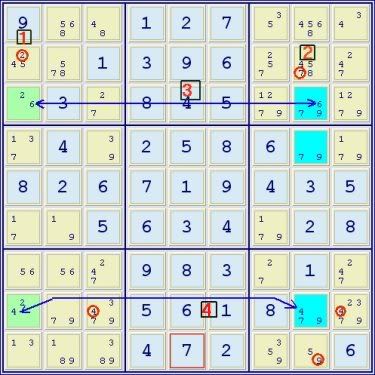
There is nothing like real-world solving examples to make potentially difficult concepts easier to grasp for newer solvers. Likewise, in this case the examples prove the perhaps unappreciated power of both ALS Chains and Doubly-Linked ALSs. The following is the solving sequence using only ALS Chains and Dual-Linked ALSs to solve an Extreme Diabolical level puzzle (SE rating above 7) starting from the point where most basic methods leave off . (However, this does not mean that this is the only way to solve this puzzle.) Note that RC below means restricted common.
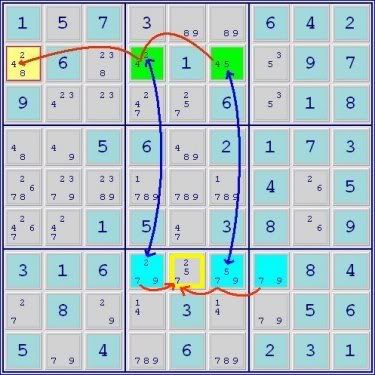
A 3-set ALS Chain
Green ALS->RC 4->Blue ALS->RC 6->Orange ALS
Orange ALS->conjugate link->yellow cell common digit for elimination 2<-Green ALS
Thus yellow cell<>2
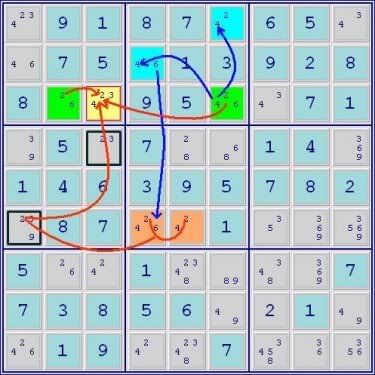
A 4-set ALS Chain
Green ALS->RC 2->Blue ALS->RC 4->Orange ALS ->RC 6->Pink ALS
Green ALS->yellow cell common digit for elimination 3<-Pink ALS
Thus yellow cell<>3
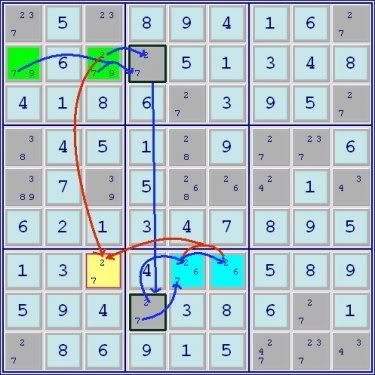
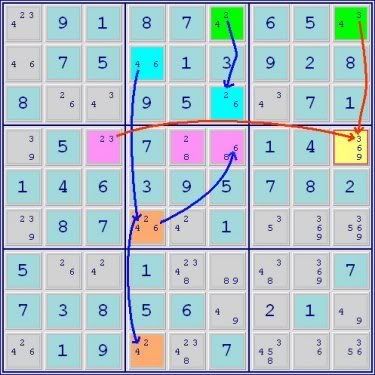
A 3-set ALS Chain
Green ALS->conjugate link->RC 6->Blue ALS->RC 3->Orange ALS
Green ALS->conjugate link->yellow cell common digit for elimination 9<-Orange ALS
Thus yellow cell<>9
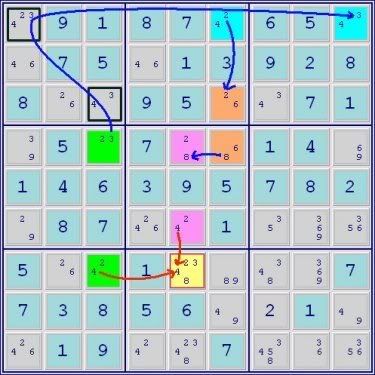
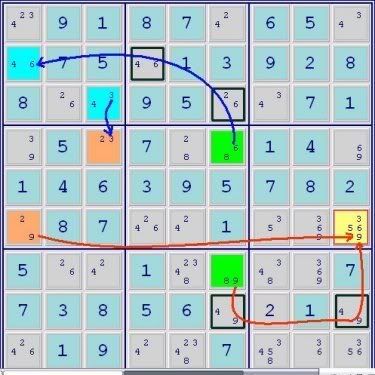
A 4-set ALS Chain
Green ALS->conjugate link->RC 3->Blue ALS->RC 2->Orange ALS->RC6->Pink ALS
Green ALS->yellow cell common digit for elimination 4<-Pink ALS
Thus yellow cell<>4
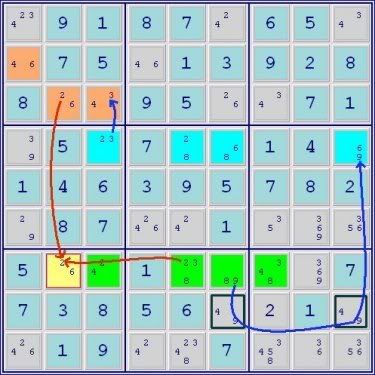
A 3-set ALS Chain
Green ALS->conjugate link->RC 9->Blue ALS->RC 3->Orange ALS
Green ALS->yellow cell common digit for elimination 2<-Orange ALS
Thus yellow cell<>2
And the puzzle is solved.
Conclusion:
ALS Chains and Doubly-Linked ALSs are extremely powerful methods of type A pattern-solving especially if conjugate pair links are used where possible. They can take up where previous basic methods leave off and can be used to help solve very difficult puzzles. Adding ALS Chains and Doubly-Linked ALSs to one's solving arsenal is not all that difficult. Some hints: When looking at examples in tutorials do not make the mistake of trying to find chains in your puzzles that look like those in the examples. It’s far better to understand the underlying principles involved and you will find ALS Chains where you never thought possible. Practice a lot initially by looking for ALS Chains in all your puzzles. Do not try to work backwards. That is, do not try to find an ALS solution for a particular digit you want to remove. That rarely works and does nothing but waste your time and wear you out. Finally, the use of a solver that allows one to color cells, such as Angus Johnson’s Simple Sudoku or Ruud’s SudoCue, can be helpful in manually tracing an ALS Chain during the solving process.
By the way: The possibility for several eliminations from doubly-linked ALSs is closely related to the several eliminations possible from Sue De Coq, a tutorial for which is available here:
http://forum.enjoysudoku.com/viewtopic.php?t=6410
(Note: ASI stands for advanced solving illustrated. Credits: The final Doubly-Linked ALS graphic is based on an example first presented by Anne Morelot in mid-2006 on the Eureka forum. The warning about not using the same restricted common values in adjacent sets comes mainly from the recent work of Paul Isaacson. Prior to that the rules concerning re-use of restricted common values were less than clear.)