The New Sudoku Players' Forum

[DonM]

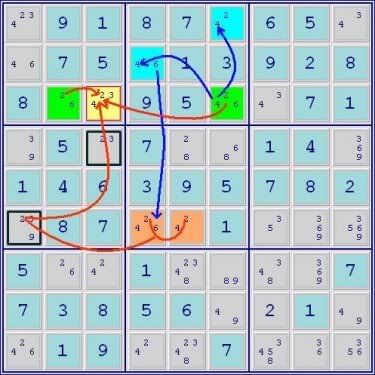
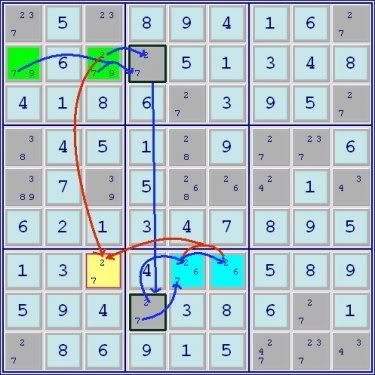
Aha, I see some trickery here with the naked pair between the two ALSs. I'll have to study that a bit more....

Seven cover sets are required for the six cells. In a true ALS doubly-linked xz-rule, the number of base sets and cover sets would be equal. Since the ALSs are not doubly-linked, if follows that there is no corresponding "restricted common elimination" either.

This appears to be a rather interesting situation where, on the surface, the description is accurate, but in the end, the example fails. Since this is meant to be accessible particularly to newer solvers, I think there is another way of looking at the problem that can be described without using base sets & cover sets which the less experienced wouldn't understand.

First, the standard restricted common definition: A digit is restricted common to 2 Almost Locked Sets when it cannot be present in both sets at the same time. In the example in question, taken separately, the 2 and the 7, through the direct conjugate links, appear to fulfill that definition. Thus, it would appear that 2 ALSs+2 restricted commons = doubly linked, but the resolution of the pattern doesn't end up working that way. The problem is that, probably unique to this type of example, the resolution of either of the restricted common links destroys the other or put another way satisfying one of the restricted commons solves for the naked pair destroying both conjugate pairs.

If this perspective is correct, maybe there needs to be some small print added to the doubly linked ALS definition that the restricted commons have to operate independently of each other or something to that effect. So, since I like to keep things simple, it appears that the 'double' conjugate link doesn't work; the base/cover set explanation likely uncovers the underlying flaw in the logic. In any event, thanks for pointing out that the example is flawed. This tutorial has to be as accurate as reasonably possible so the graphic will be replaced.

[PIsaacson]

Therefore, it is important to note that when searching out the components of ALS Chains of greater than 2 sets, the restricted commons in the chain must have different values for the chain to result in a valid elimination. For instance, it is easy to make the mistake of having a restricted common, say 5, between two sets in the first part of a chain and then find another apparent restricted common 5 between two sets later in the chain. However, such a chain will result in an invalid elimination.

Don,

I'm glad that you included that warning. When I first coded the ALS chaining method for my solver, I ran into this and SirDave patiently explained the error in my logic. I excluded re-using common restricted digits in building ALS chains, and this effectively constrained them to a length of 9. Manually, I'm lucky if I can spot an ALS chain longer than 3, but my C++ solver often displays ALS chains of size 5-6. I have often wondered if the re-use clause is valid for the entire chain, or just for adjacent links which is what my original problem encountered. Is it possible to prove that this is absolutely true for any length ALS chain? The reason I ask is that if I could lift this restriction, my solver might find really looooong ALS chains.

Second question(s): The naked pair conjugate link looks somewhat like an x-cycle on the digit 2. Is there some fine point I'm missing here?

r7c3 = 2 => r7c56 <> 2 => r8c4 = 2 => r2c4 <> 2 => r2c3 = 3, contradiction so r7c3 <> 2

Please excuse my logic chain notation. I never did master AIC/niceloop or Eureka encoding. Was the intent to use the naked pair as a dual hinge or something equivalent? I never quite understood this part of the ALS chain write-up as it implied using naked pairs to "extend the reach" of the ALS candidates. It seems logical since any conjugate pair is a strong link and should be capable of "extending" a chain. I use ALSs as group extensions in Denis's nrczt chains, so why shouldn't ALS chains be allowed to have weak/strong links to "stitch" them together? Or is that just niceloops with embedded ALS groups?

Regardless of the answers, thanks for reviving one of the more interesting and powerful techniques. And it fits in well with Sue deCoqs as it's often another way of looking at and finding SDCs, and vice versa.

[ronk]

I have often wondered if the re-use [edit: of restricted common digits] clause is valid for the entire chain, or just for adjacent links which is what my original problem encountered. Is it possible to prove that this is absolutely true for any length ALS chain?

Since one can re-use "weak-link digits" in an xy-chain, I seriously doubt it. Why should an ALS chain be any different?

[DonM]

Therefore, it is important to note that when searching out the components of ALS Chains of greater than 2 sets, the restricted commons in the chain must have different values for the chain to result in a valid elimination. For instance, it is easy to make the mistake of having a restricted common, say 5, between two sets in the first part of a chain and then find another apparent restricted common 5 between two sets later in the chain. However, such a chain will result in an invalid elimination.

Don,

....Manually, I'm lucky if I can spot an ALS chain longer than 3, but my C++ solver often displays ALS chains of size 5-6. I have often wondered if the re-use clause is valid for the entire chain, or just for adjacent links which is what my original problem encountered. Is it possible to prove that this is absolutely true for any length ALS chain? The reason I ask is that if I could lift this restriction, my solver might find really looooong ALS chains.

I have never seen any guidelines that, if followed, would allow the reliable re-use of a restricted common and a valid exclusion. Therefore, best to avoid the practice. However, my guess is that with an ALS chain of 6 to 8 sets, you would be running up against the useful limits of the pattern anyway.

Second question(s): The naked pair conjugate link looks somewhat like an x-cycle on the digit 2. Is there some fine point I'm missing here?

r7c3 = 2 => r7c56 <> 2 => r8c4 = 2 => r2c4 <> 2 => r2c3 = 2 [3 minor typo], contradiction so r7c3 <> 2

Please excuse my logic chain notation. I never did master AIC/niceloop or Eureka encoding.

No, you're not missing anything. The exclusion r7c3<>2 is correct, but the basis for it in the example was incorrect. Your description above can be expressed:

AIC: grp(2)r7c67 = r8c4 - r2c4 = (2)r2c3
NL: r7c3 -2- r7c67 =2= r8c4 -2- r2c4 =2= r2c3 -2- r7c3

=> r7c3<>2

Was the intent to use the naked pair as a dual hinge or something equivalent? I never quite understood this part of the ALS chain write-up as it implied using naked pairs to "extend the reach" of the ALS candidates. It seems logical since any conjugate pair is a strong link and should be capable of "extending" a chain. I use ALSs as group extensions in Denis's nrczt chains, so why shouldn't ALS chains be allowed to have weak/strong links to "stitch" them together? Or is that just niceloops with embedded ALS groups?

You're correct about the intent as far as that example goes, but only that example. It seemed logical that a double link could occur through a double conjugate pair, but the actual implementation doesn't work for doubly-linked ALSs. However, I want to clarify that it is conjugate pairs that can extend the reach, not naked pairs. Using examples that clearly illustrate a pattern has its limitations. One of those is that for most of the examples where this 'extended reach' was shown, the conjugate pair happened to exist with another pair (aka forming a naked pair), but the other pair didn't have any purpose in the chain.

I don't think you need help with the conjugate pair premise, but just to make sure that it is clear that naked pairs were never supposed to be part of the overall equation (other than the flawed exception just above), take a look at this example from the tutorial:



The conjugate pair of 2s (r4c3, r6c1) allows the 2s in the Orange set to see the 2 in the elimination cell just the same as if they were in a direct line of sight and in this example there are no naked pairs.

Regarding, the point about group nice loops- that was mentioned at the beginning of the tutorial. As presented here, ALS Chains can be used for pattern solving in its purest form (aka pattern A solving). But beyond that, learning to identify ALS Chains can also be helpful in making the best use of ALS patterns in AICs/nice loops. Still, separate from all that, the ALS Chains above can be expressed in a myriad of different ways when it comes to AICs/nice loops including ALSs+groups etc.

Regardless of the answers, thanks for reviving one of the more interesting and powerful techniques. And it fits in well with Sue deCoqs as it's often another way of looking at and finding SDCs, and vice versa.

I appreciate it.

[PIsaacson]

Since one can re-use "weak-link digits" in an xy-chain, I seriously doubt it. Why should an ALS chain be any different?

I hate to acknowledge my ignorance, but I surrender. What is a weak-link doing in an XY-chain? I thought they were composed entirely of strong links with bi-value/bi-local conjugate pairs.

I agree (I think) that this definition of ALS-chains seems similar to XY-chains in the sense that restricted common digits form strong links between the ALSs and the various CECs are weak link eliminations. If they are truly not different, and re-using RCDs (Restricted Common Digits - another TLA!) is permissible (under what conditions?), then could you form ALS loops with their extended ability to eliminate on each axis? Or is that an invalid/impossible condition?

Since I'm out of my league in terms of mathematical or logical proofs, I may just modify my code and back-test against large puzzle sets to see what happens.

[ronk]

Since one can re-use "weak-link digits" in an xy-chain, I seriously doubt it. Why should an ALS chain be any different?

What is a weak-link doing in an XY-chain? I thought they were composed entirely of strong links with bi-value/bi-local conjugate pairs.

In some circles, chains made purely of bi-locals are termed x-cycles, and chains made purely of bi-values are termed y-cycles. In these circles, it is reasonable to expect xy to indicate the presence of both, so I understand your confusion. However, a chain made purely of bi-values is most commonly referred to as an xy-chain on this forum.

Bi-value and bi-location strong inferences (links) of useful chains are always connected by weak inferences. Hence the term alternating inference chains (AICs). For nice loop notation, inferences within cells -- both strong and weak -- are not explicitly expressed, but implied.

I have no way to search for long ALS chains, so the best I can do is convert portions of an xy-chain into ALSs. In the conversion below, you can see that digit 7 appears twice as a restricted common. The puzzle is from Mike Barker's first post here.

Code: Select all

..65.....18..4.9.5......3....846.5....2.....4.59.8..6......614..3....6.......7.83

After SSTS:
 279  79-2 6    | 5    3   B19   | 4   A12   8
 1    8    3    | 6    4    2    | 9    7    5
 259  249  45   | 179  179  8    | 3    12   6
----------------+----------------+--------------
E37  D17   8    | 4    6   C19   | 5    39   2
F36   16   2    | 179  179  5    | 8    39   4
 4    5    9    | 2    8    3    | 7    6    1
----------------+----------------+--------------
 8   J29  H57   | 3    25   6    | 1    4   I79
 29   3    17   | 8    12   4    | 6    5    79
G56   46   145  | 19   159  7    | 2    8    3

As a pure xy-chain:
          A        B        C        D        E        F        G        H        I        J
r1c2 -2- r1c8 -1- r1c6 -9- r4c6 -1- r4c2 -7- r4c1 -3- r5c1 -6- r9c1 -5- r8c3 -7- r8c9 -9- r8c2 -2- r1c2

As an als-chain:
             AB            CD            EFG         H           IJ
r1c2 -2- als:r1c68 -9- als:r4c26 -7- als:r459c1 -5- r8c3 -7- als:r8c29 -2- r1c2

Each implies r1c2<>2

If they are truly not different, and re-using RCDs (Restricted Common Digits - another TLA!) is permissible (under what conditions?), then could you form ALS loops with their extended ability to eliminate on each axis? Or is that an invalid/impossible condition?

I don't know the "conditions" one would use in a computerized search. I recall Mike Barker posting a definition in this forum, but can't find it now. [edit: OTOH that definition may have been about ALS overlap, related but probably not the same.] I have no idea what you mean by "eliminate on each axis."

Since I'm out of my league in terms of mathematical or logical proofs, I may just modify my code and back-test against large puzzle sets to see what happens.

Seems reasonable to me.

[PIsaacson]

Ronk,

Thanks for clearing up my confusion with XY chains. I had recently studied Glenn Fowler's X/Y cycles and used them in 3dmedusa, so my bad. My reference to an axis of elimination comes from http://forum.enjoysudoku.com/viewtopic.php?t=2966 It was a poor choice of words, again my bad.

On the testing front, I modified my ALS-chain method to either use the former "no RCD re-use" rule or the new and improved "no RCD adjacent" rule which allows a qualified re-use. The long and short seems to be that this works and provides (some) additional ALS chains that would have otherwise been invalid. I've run tests against the top1465 and I'm working on the top50000. Here's my preliminary findings:

Top1465 using ALS-chain after SSTS and no other advanced solving techniques

1) Old rule - 840 solved with 7595 ALS chains resulting in 10207 eliminations at 49 msec/reduction and 10 size 7 and 2 size 8.

2) New rule - 841 solved with 7649 ALS chains resulting in 10274 eliminations at 53 msec/reduction and 24 size 7, 3 size 8 and 1 size 9.

Not a particularly impressive increase in power, but at least one additional puzzle was solved. I'll post the top50000 when I have those results.

Using Mike Barker's example puzzle, my solver found the following ALS chains after SSTS:

Code: Select all

Puzzle: ..65.....18..4.9.5......3....846.5....2.....4.59.8..6......614..3....6.......7.83

 279       279       6        |5         3         19       |4         12        8
 1         8         3        |6         4         2        |9         7         5
 259       249       45       |179       179       8        |3         12        6
 --------- --------- ---------+--------- --------- ---------+--------- --------- ---------
 37        17        8        |4         6         19       |5         39        2
 36        16        2        |179       179       5        |8         39        4
 4         5         9        |2         8         3        |7         6         1
 --------- --------- ---------+--------- --------- ---------+--------- --------- ---------
 8         29        57       |3         25        6        |1         4         79
 29        3         17       |8         12        4        |6         5         79
 56        46        145      |19        159       7        |2         8         3

ALS-chain results with the rule that no RCD can be re-used:


als[4x7] b1x1289.<24579> =5= r3c12458.<124579> =4= b7x234678.<1245679> =1= r8c15.<129>
reducing r3c1.<259> by <9>

als[4x5] r1c168.<1279> =7= r1379c2.<24679> =6= b7x247.<2569> =5= r7c239.<2579>
reducing r1c2.<279> by <2>

als[3x5] b1x1789.<24579> =7= r4c168.<1379> =1= r1c6.<19>
reducing r1c2.<79> by <9>

als[5x4] r17c2.<279> =7= r4c26.<179> =9= r1c68.<129> =2= r345c8.<1239> =1= r3c45.<179>
reducing r3c2.<249> by <9>


ALS-chain results with the rule that an RCD cannot be adjacent, but can be re-used:


als[4x7] b1x1289.<24579> =5= r3c12458.<124579> =4= b7x234678.<1245679> =1= r8c15.<129>
reducing r3c1.<259> by <9>

als[4x5] r1c168.<1279> =7= r1379c2.<24679> =6= b7x247.<2569> =5= r7c239.<2579>
reducing r1c2.<279> by <2>

als[3x5] b1x1789.<24579> =7= r4c168.<1379> =1= r1c6.<19>
reducing r1c2.<79> by <9>

als[5x4] r147c2.<1279> =1= r4c6.<19> =9= r1c68.<129> =2= r345c8.<1239> =1= r3c45.<179>
reducing r3c2.<249> by <9>

Same eliminations, but the new rules allowed for the re-use of the RCD 1 as the first and last within the final size 5 ALS chain. I'm starting to think that there are so many ALSs available, that the no re-use restriction hardly matters. I'm more interested in trying to see if an ALS loop can provide the additional eliminations similar to an XY-loop.

[tarek]

I'm more interested in trying to see if an ALS loop can provide the additional eliminations similar to an XY-loop

Well, the mutual exclusion rule should be the example .... I tried to make a diagram some time ago for the ALS-XY mutual exclusion rule (essentially a 3 ALS loop)

Happy hunting ... The results will be impressive

tarek

[PIsaacson]

Tarek,

My lack of understanding can never be under estimated. Could you please explain what you mean by the rule of mutual exclusion or send me a thread url to review?

Thanks,
Paul

[aran]

I have often wondered if the re-use [edit: of restricted common digits] clause is valid for the entire chain, or just for adjacent links which is what my original problem encountered. Is it possible to prove that this is absolutely true for any length ALS chain?

Since one can re-use "weak-link digits" in an xy-chain, I seriously doubt it. Why should an ALS chain be any different?

Further to that :
Use the following terminology
z : elimination candidate in the Candidate Elimination Cell
S1=first set, S2=second set etc
R1 = restricted common (RC) between S1 and S2 etc
e=all candidates other than z and RC (note : e can be 0,1 or several candidates).

Also note : what is important in the mechanism is not the number of cells in the sets but their candidate composition, thus for example the dual set (2,3) (3,5) can be reduced to the single entity {2,3,5}

Given the above, an ALS chain progressed by restricted commons with target z in some CEC can therefore be presented as :
{z,e,R1} {R1,e,R2} {R2,e,R3}…..{RN-2,e,RN-1} {RN-1,e,z}.

As we know the mechanism is : zCEC true locks S1, which locks S2 via the RC, which locks S3 etc….which locks SN ie SN is the locked set {e,z} which zCEC then overlocks : hence <z> CEC.

From the above we can draw the following conclusions :
- (P Isaacson’s original question} : adajacent RCs cannot be identical eg if R1=R2, then S2 is reduced to {e} since R1 sees all instances of R1=R2 in S2 by definition. And {e} is necessarily locked and stops chain progression.
- no theoretical reason why non-adjacent RCs cannot be identical ie no block on non-adjacent re-use
- when reduced to its minimal expression the above general form becomes : {z,R1} {R1,R2} {R2,R3}…..(RN-2,RN-1} {RN-1,z} ie the XY-chain to which Ronk refers. Very clear here that adajacent RCs cannot be identical (otherwise the bivalue is a placement, and couldn’t have been in the chain to begin with)

As to ALS loops in this context (P Isaacson question) and subject to rescrutiny :
with a loop, we have S1={z,e,R1} and SN = {RN-1,e,z} with SN then looping to S1.
=> zCEC is still eliminated as above.
=> via AIC : zS1=R1S1-R1S2=S2locked-R2S3…..-RN-1SN=SNlocked (e,z) :
then the loop link from locked SN overlocks S1 : contradiction, hence z is true in S1 which is either a placement if z occurred only once in S1 or a limitation on z to the cells in S1.

[ronk]

As to ALS loops in this context (P Isaacson question) and subject to rescrutiny :
with a loop, we have S1={z,e,R1} and SN = {RN-1,e,z} with SN then looping to S1.
=> zCEC is still eliminated as above.
=> via AIC : zS1=R1S1-R1S2=S2locked-R2S3…..-RN-1SN=SNlocked (e,z) :
then the loop link from locked SN overlocks S1 : contradiction, hence z is true in S1 which is either a placement if z occurred only once in S1 or a limitation on z to the cells in S1.

Do you have a less obfuscatory version? And what the heck is overlocked?

[StrmCkr]

the move in question using 3 pairs of 7/2 with the interaction of 2 als sets linked

seems to me it functions in the same manerism as the move i call "remote triple" (due to the als set involved)



with the exception i would mark go off both the pairs in box2 & 8.
removing the 7&2 from R2C3

seen as a kraken:

(7)R7C5 - (2)R7C3 - (7)R3C5-(2)R2C4 => R2C3<>2,7
|
(2)R7C5 - (7)R7C3 - (2)R3C5-(7)R2C4 =>R2C3<>2,7
|
(6)R7C5 - (2)R7C6 - (7)R8C4-(2)R2C4 - (7)R7C3 =>R2C3<>2,7

or it looks like this.

where x <>2,7

Code: Select all

X(box1) -------- (72)(box2)
|                        |       \
|                        |     (72)(box2)
|                        |        |
|                        |        |
|                        |        |
(72)(box7) --------------| -------(267)(box8) ----(26) (box8)
                         |           /          /
                         |          /       /
                         |        /   /
                         (27)(box8)       

[PIsaacson]

top50000 results:

1) Old ALS RCD rules: 35747 solved with 475282 ALS chains resulting in 569390 eliminations at 19 msec/reduction and 1163 size 7, 92 size 8 and 5 size 9.

2) New ALS RCD rules: 41005 solved with 618588 ALS chains resulting in 749733 eliminations at 24 msec/reduction and 3410 size 7, 504 size 8, 87 size 9, 16 size 10, 3 size 11, and 1 size 12.

There were no invalid eliminations caused by the new adjacency rule and these results look subjectively more "promising" than the top1465 results.

I'm not sure if these tests are sufficiently exhaustive to accept this as truly conclusive, so I defer to Ronk's and aran's replies. I still puzzling over them and I don't want to declare victory on my own findings, but I think (hope?) they concur.

Ronk,

I especially want to thank you for pointing me back to XY-chains and how to view them as AICs. I also like your ALS chain notation. Is that part of the AIC accepted standard? I need to master one of AIC, niceloop or Eureka. I'm still looking at your chains and I like starting the CEC as a weak link into the ALS, so I'm guessing that the missing strong link (AIC is all about alternating weak/strong links?) is within the ALS as it becomes a locked set? Which cascades as the RC acts as the next weak link into the following ALS...? I think that's what aran proved, but I'm still going over his final statements.

aran,

Since an XY chain consists of bi-value cells which are implicitly ALSs, shouldn't ALS chaining subsume XY chaining? I think the answer is yes, but I'm not 100% sure because otherwise ALS loops should be allowed as well since XY loops are a valid construct. So I'm not sure I follow your final logic. Are you saying that ALS loops are truly impossible? If so, then how do XY loops exist? Thanks to Ronk, I'm now looking at XY chains as ALS chains composed entirely of bi-value ALS cells. Is this POV completely off-base?

[tarek]

you please explain what you mean by the rule of mutual exclusion or send me a thread url to review?

Hi Paul,

What I referred to is something that you already know ... It is the ALS-xz rule with 2 restricted commons (doubly weakly linked) ...It can be thought of as being a loop.

the urls:
http://forum.enjoysudoku.com/viewtopic.php?t=3979
http://forum.enjoysudoku.com/viewtopic.php?t=2471

Here is my modified diagram for a 3 ALS loop

Code: Select all

                     ...*BA2....
                    .           .
                   .             .
                  .               .
               BA2.................BA2
                /                   \
               /                     \
*b.......b----B           A           C----c.......c*
              |\         /.\         /|
              | x.......x . y.......y |
              | .       . . .       . |
              |  .     .  .  .     .  |   
              |   .   .   .   .   .   |
              z    *x     *a   *y     z
               .                     .
                .                   .
                 .........*z........

x,y,BA2: Restricted commons
*: Possible eliminations

tarek

[aran]

As to ALS loops in this context (P Isaacson question) and subject to rescrutiny :
with a loop, we have S1={z,e,R1} and SN = {RN-1,e,z} with SN then looping to S1.
=> zCEC is still eliminated as above.
=> via AIC : zS1=R1S1-R1S2=S2locked-R2S3…..-RN-1SN=SNlocked (e,z) :
then the loop link from locked SN overlocks S1 : contradiction, hence z is true in S1 which is either a placement if z occurred only once in S1 or a limitation on z to the cells in S1.

Do you have a less obfuscatory version? And what the heck is overlocked?

Ronk, you mean you want to give me {z, e, R0} for all of that...
"Overlocked" is just a personal term reflecting on how I actually think about the ALS-xz or any ALS-chain type elimination mechanism. ie z starts off a chain of locks (locked sets) which produces a final locked set which z with its all-seeing eye then overlocks (ie further locks a locked set) => contradiction=><z>.

PIsaacson

Ronk,

I especially want to thank you for pointing me back to XY-chains and how to view them as AICs. I also like your ALS chain notation. Is that part of the AIC accepted standard? I need to master one of AIC, niceloop or Eureka. I'm still looking at your chains and I like starting the CEC as a weak link into the ALS, so I'm guessing that the missing strong link (AIC is all about alternating weak/strong links?) is within the ALS as it becomes a locked set? Which cascades as the RC acts as the next weak link into the following ALS...? I think that's what aran proved, but I'm still going over his final statements.

At the great risk of stating the obvious, there is no such thing as a chain (no matter what name it bears) without alternating links. Any chain necessarily consists of a series of alternating links, and if you see one that doesn’t respect this pattern, then either there is an abbreviation (eg in some of that not nice nice loop notation) or it doesn’t hold water.
When chains branch, it just means that at the branching point there is more than one candidate for the strong link (“true”) and so each “true” line is followed on the alternating link basis, and if these don’t link up on and agree somewhere, end of story.
So starting with a weak link from the CEC just means : if z in CEC is true, then z is false in the first ALS set which is therefore locked, ie all the locked digits are true, including the restricted common, which is therefore false in the next ALS set, which is therefore locked, so the next restricted common is true there, so it is false in the following set and so on. This is the alternating pattern you were asking about.

aran,

Since an XY chain consists of bi-value cells which are implicitly ALSs, shouldn't ALS chaining subsume XY chaining? I think the answer is yes, but I'm not 100% sure because otherwise ALS loops should be allowed as well since XY loops are a valid construct. So I'm not sure I follow your final logic. Are you saying that ALS loops are truly impossible? If so, then how do XY loops exist? Thanks to Ronk, I'm now looking at XY chains as ALS chains composed entirely of bi-value ALS cells. Is this POV completely off-base ?

Entirely right, XY chains are subsumed. They aren’t even “implicitly” ALS chains, they are explicitly so.
My point about ALS loops was meant to be this :
- whether there is or isn’t a loop, the basic zCEC elimination works
- if there is a loop then we have a chain which boils down to zSet1=…..=zSet1 ie if z is false in Set1, then it is true in Set 1 : conclusion z must be true in Set 1. The consequence then depends on the distribution of z in Set 1 : if it is in one cell only, it can be placed. If it is in two sets for example, then it can be removed from anything seen by both.