I'm not even sure I consider the original ALS presentation cannibalistic since killing the eights in r789c4 does not render any of the whole premises above false. Perhaps it's just a flesh wound
Almost Locked Sets xz-rule (doubly-linked)
(2&8&9=5)r123c4 - (5=1&6&7&8&9-1&5&6&7&8=9)r789c4|r9c56 - (9=2&5&8)r123c4...loop
I'm not even sure I consider the original ALS presentation cannibalistic since killing the eights in r789c4 does not render any of the whole premises above false. Perhaps it's just a flesh wound
I'm not even sure I consider the original ALS presentation cannibalistic since killing the eights in r789c4 does not render any of the whole premises above false. Perhaps it's just a flesh wound
- Myth Jellies
- Posts: 593
- Joined: 19 September 2005
Myth Jellies wrote:I'm not even sure I consider the original ALS presentation cannibalistic since killing the eights in r789c4 does not render any of the whole premises above false. Perhaps it's just a flesh wound
As the cannibal term is being used on this forum, I believe that's always the case. I use the term but don't like it and would quickly switch to a truly better one.
- ronk
- 2012 Supporter
- Posts: 4764
- Joined: 02 November 2005
- Location: Southeastern USA
I posted the following puzzle here for a Nice Loop Question, but after adding Doubly Linked ALS-XZ to my solver (after a little nudge by ronk and PIsaacson) I found an ALS-XZ with 6 cells and 16 eliminations:
After singles:
- Code: Select all
3.2....1....97.............5...8.6....15...7..8..4....9....1.27.1.4.......5..79..
After singles:
- Code: Select all
.-----------------------.-------------------------------.-------------------------.
| 3 45-679 2 | A68 A56 45-68 | 4578 1 45-689 |
| 1 456 468 | 9 7 2345-68 | 23458 34568 234568 |
| 4678 45679 46789 | 23-6-8 1 2345-68 | 234578 345689 2345689 |
:-----------------------+-------------------------------+-------------------------:
| 5 23479 3479 | 1 8 239 | 6 349 2349 |
| 246 23469 1 | 5 2369 2369 | 2348 7 23489 |
| 26 8 369 | 7 4 2369 | 1 359 2359 |
:-----------------------+-------------------------------+-------------------------:
| 9 346 3468 | B368 B356 1 | 3458 2 7 |
| 2678 1 3678 | 4 -2-3-5-69 -2-35-689 | 358 3568 3568 |
| -2468 -2346 5 | B2368 B236 7 | 9 3468 1 |
'-----------------------'-------------------------------'-------------------------'
Almost Locked Set XZ-Rule: A=r1c45 - {568}, B=r7c45,r9c45 - {23568}, X=5,8, Z=5,8 => r8c56,r9c12<>2, r8c56<>3, r8c5<>5, r1c269,r238c6,r3c4,r8c5<>6, r3c4<>8
- hobiwan
- 2012 Supporter
- Posts: 321
- Joined: 16 January 2008
- Location: Klagenfurt
This puzzle has a nice opening move! The puzzle:
After a Hidden Single and a Locked Candidates move:
- Code: Select all
.........2.....3495...3926..9.........41...8....598..4..182...6......7....3..6...
After a Hidden Single and a Locked Candidates move:
- Code: Select all
.--------------------------------.-------------------------.--------------------.
| -1346-7-89 -1346-7-8 6-7-89 | 246-7 146-78 124-7 | 158 157 1578 |
| 2 B1678 B678 | A67 15-6-78 15-7 | 3 4 9 |
| 5 B1478 B78 | A47 3 9 | 2 6 178 |
:--------------------------------+-------------------------+--------------------:
| 13678 9 25678 | 2346-7 467 2347 | 156 12357 12357 |
| 367 23567 4 | 1 67 237 | 9 8 2357 |
| 1367 -12367 267 | 5 9 8 | 16 1237 4 |
:--------------------------------+-------------------------+--------------------:
| 479 457 1 | 8 2 3457 | 45 359 6 |
| 4689 24568 25689 | 349 145 1345 | 7 12359 12358 |
| 4789 24578 3 | 4-79 1457 6 | 1458 1259 1258 |
'--------------------------------'-------------------------'--------------------'
Almost Locked Set XZ-Rule: A=r23c4 {467}, B=r2c23,r3c23 {14678}, X=4,6, Z=6 => r1c12,r6c2<>1, r2c5<>6, r1c123456,r2c56,r49c4<>7, r1c123<>8
- hobiwan
- 2012 Supporter
- Posts: 321
- Joined: 16 January 2008
- Location: Klagenfurt
I wanted to post this in case it hasn't been made obvious before. If so, forgive my effrontery...
There are at least 3 paths for generating dual-linked ALS pairs:
1) The ALS XZ dual-linked method which involves 2 ALSs that are directly linked by 2 RCDs.
2) The Death Blossom method which involves 2 ALSs that are linked by a bi-local conjugate pair as one RCD, and then directly linked by another RCD thus forming a dual-linked pair.
3) Any ALS chain where the start/end ALSs are directly linked by another RCD. This includes DBs with bi-value stems since they can be viewed as simple ALS chains of length 3. These can also be viewed as ALS loops.
Types (1) and (2) are relatively more common, but Type (3) start entering into the picture when you locate longer ALS chains. In addition, Type (3) ALS chains of length > 2 may produce additional eliminations from component sub-chain segments.
That's a really pretty dual-linked ALS chain! My ALS base/cover claims that in addition to the 17 eliminations from standard dual-linked rules, r3c9<>7 due to (67r2, 47r3, 1c2, 8b1).
There are at least 3 paths for generating dual-linked ALS pairs:
1) The ALS XZ dual-linked method which involves 2 ALSs that are directly linked by 2 RCDs.
2) The Death Blossom method which involves 2 ALSs that are linked by a bi-local conjugate pair as one RCD, and then directly linked by another RCD thus forming a dual-linked pair.
3) Any ALS chain where the start/end ALSs are directly linked by another RCD. This includes DBs with bi-value stems since they can be viewed as simple ALS chains of length 3. These can also be viewed as ALS loops.
Types (1) and (2) are relatively more common, but Type (3) start entering into the picture when you locate longer ALS chains. In addition, Type (3) ALS chains of length > 2 may produce additional eliminations from component sub-chain segments.
That's a really pretty dual-linked ALS chain! My ALS base/cover claims that in addition to the 17 eliminations from standard dual-linked rules, r3c9<>7 due to (67r2, 47r3, 1c2, 8b1).
- PIsaacson
- Posts: 249
- Joined: 02 July 2008
PIsaacson wrote:I wanted to post this in case it hasn't been made obvious before. If so, forgive my effrontery...
There are at least 3 paths for generating dual-linked ALS pairs:
1) The ALS XZ dual-linked method which involves 2 ALSs that are directly linked by 2 RCDs.
2) The Death Blossom method which involves 2 ALSs that are linked by a bi-local conjugate pair as one RCD, and then directly linked by another RCD thus forming a dual-linked pair.
3) Any ALS chain where the start/end ALSs are directly linked by another RCD. This includes DBs with bi-value stems since they can be viewed as simple ALS chains of length 3. These can also be viewed as ALS loops.
Paul, I'm finding this terminology rather confusing. In my mind, the ALS xz dual-linked method is a particular pattern that gives rise to a unique set of potential eliminations, different than 'regular' ALS Chains or DBs and the term, dual or doubly linked derives from the fact that 2 ALSs share two RCDs which isn't the case with the other patterns. Also, I'm not at all following the concept of DBs as dual-linked: 2 ALSs don't share the same 2 RCDs which can give raise to several eliminations, but rather a 'central' stem cell connects with each petal set thru its own separate RCD giving rise to, usually, a single elimination (if the 'simple' DB with a central bivalue cell is looked on as a 3-set ALS Chain, as I usually see it, then the difference is still the same). Putting them all under the umbrella term of dual/doubly linked would seem to be mixing different patterns.
As usual, I could be missing something.
Last edited by DonM on Wed Apr 15, 2009 1:24 am, edited 1 time in total.
- DonM
- 2013 Supporter
- Posts: 487
- Joined: 13 January 2008
PIsaacson wrote:That's a really pretty dual-linked ALS chain! My ALS base/cover claims that in addition to the 17 eliminations from standard dual-linked rules, r3c9<>7 due to (67r2, 47r3, 1c2, 8b1).
But that's for different sets for a different doubly-linked ALS xz-rule.
als:r2c234 -1- als:r3c234 -8- als:r2c234 - continuous loop
IMO the eliminations for ALS xz-rule deductions are generally being overstated. Where is it written that the deductions for one ALS-xz step shall be the superposition of all possible combinations of base sets and cover sets?
- ronk
- 2012 Supporter
- Posts: 4764
- Joined: 02 November 2005
- Location: Southeastern USA
Don,
I know this sounds confusing if not crazy, but I think we need to consider dual-linked ALSs as a separate entity. Imagine that two ALSs are linked via two RCDs from different nice-loop paths. Then regardless of the distance of separation (path length), as long as they are dual-linked they can provide all the eliminations that would result from the normal dual-linked rules. Replace "nice-loop paths" in the above sentence with "DB bi-value/bi-local stems" or "intermediate ALS chains" and you'll see my point. It doesn't matter how they are dual-linked, it just matters that they are.
I've already got types (1), (2) and (3) working in my ALS engine, so I guess I should release an update for those who might want to explore this first hand. I also have numerous examples of all 3 types for Xsudo analysis and I'm debugging the nice-loop chaining. The to-do list keeps growing, and growing, and growing...
Ron,
The stated r3c9<>7 was from the described 6 cells as the base set with the cover set (67r2, 47r3, 1c2, 8b1). I don't understand your reference to "that's for different sets..." Your ALS loop is the exact same 6 cells, just from a different POV. My base/cover logic doesn't consider how the base cells were located, it just treats them as one single base set. It is completely de-coupled from the process of finding such sets of cells for consideration.
I'll concede that it is not "written that the deductions for one ALS-xz step shall be...", but where is it written that it is forbidden to look for them? I have this desire/need to find the maximum mileage from a given set of cells/candidates regardless of the techniques used for discovery. I've written some code that finds all possible combinations of cover sets for any given set of base cells, and it's finding some really interesting (and exhaustive) sets of eliminations. Yikes!!! That sounded perilously close to self-serving egotism!!! It's just an attempt to explain where I'm coming from/going to...
Cheers,
Paul
I know this sounds confusing if not crazy, but I think we need to consider dual-linked ALSs as a separate entity. Imagine that two ALSs are linked via two RCDs from different nice-loop paths. Then regardless of the distance of separation (path length), as long as they are dual-linked they can provide all the eliminations that would result from the normal dual-linked rules. Replace "nice-loop paths" in the above sentence with "DB bi-value/bi-local stems" or "intermediate ALS chains" and you'll see my point. It doesn't matter how they are dual-linked, it just matters that they are.
I've already got types (1), (2) and (3) working in my ALS engine, so I guess I should release an update for those who might want to explore this first hand. I also have numerous examples of all 3 types for Xsudo analysis and I'm debugging the nice-loop chaining. The to-do list keeps growing, and growing, and growing...
Ron,
The stated r3c9<>7 was from the described 6 cells as the base set with the cover set (67r2, 47r3, 1c2, 8b1). I don't understand your reference to "that's for different sets..." Your ALS loop is the exact same 6 cells, just from a different POV. My base/cover logic doesn't consider how the base cells were located, it just treats them as one single base set. It is completely de-coupled from the process of finding such sets of cells for consideration.
I'll concede that it is not "written that the deductions for one ALS-xz step shall be...", but where is it written that it is forbidden to look for them? I have this desire/need to find the maximum mileage from a given set of cells/candidates regardless of the techniques used for discovery. I've written some code that finds all possible combinations of cover sets for any given set of base cells, and it's finding some really interesting (and exhaustive) sets of eliminations. Yikes!!! That sounded perilously close to self-serving egotism!!! It's just an attempt to explain where I'm coming from/going to...
Cheers,
Paul
- PIsaacson
- Posts: 249
- Joined: 02 July 2008
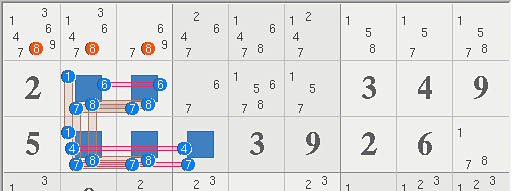
Nice ALS group, when I place the last set, the grid lights up like a neon sign.
I have tried to take it apart to see whats inside and how it relates to ALS rules. What I found was:
A 19 Eliminations: the original 17, Paul's r3c9<>7 and an extra r2c2<>7
B A small 3 cell subgroup that eliminates 7<>r2c2.
r3c3-7-als:(678)r2c34 -8- r3c3 ==> r2c2<>7 , rank 1 loop
C Six rank 0 cover set groups that eliminate a variety of candidates. All of these can be described as dual linked ALS assuming two groupings: A=r23c23 B=r23c4 or A=r2c234 and B=r3c234.
D And this 5 cell, rank 1 group , 5 sets {2N23 3N234} + 6 links {6r2 47r3 178b1} => 3 Eliminations r1c123<>8
r3c4 -7- als:(14678)r23c23 -4- r3c4 => r1c123<>8 , rank 1 loop
This one drew my attention (see diagram below) because, however the ALS's are grouped, digits 8 and 1 would be RCDs at the same time (it seems). However, only the 8s in b1 are cleared. I was curious fow ALS rules account for this?
In terms of cover sets (only) 8b1 is rank 0 because of the overlap of cover sets at 7r3c23 (a triplet), thus eliminating the 8s.
I have tried to take it apart to see whats inside and how it relates to ALS rules. What I found was:
A 19 Eliminations: the original 17, Paul's r3c9<>7 and an extra r2c2<>7
B A small 3 cell subgroup that eliminates 7<>r2c2.
r3c3-7-als:(678)r2c34 -8- r3c3 ==> r2c2<>7 , rank 1 loop
C Six rank 0 cover set groups that eliminate a variety of candidates. All of these can be described as dual linked ALS assuming two groupings: A=r23c23 B=r23c4 or A=r2c234 and B=r3c234.
- Code: Select all
Rank 0, 6 base + 6 cover sets
{2N234 3N234}+{4r3 6r2 178b1 7b2} => 14 Elim r1c123456<>7, r1c123<>8, r1c12<>1, r2c56<>7, r2c5<>6,
{2N234 3N234}+{4r3 6r2 7c4 178b1} => 12 Elim r1c1234<>7 , r1c123<>8, r1c12<>1, r49c4<>7, r2c5<>6,
{2N234 3N234}+{4r3 6r2 1c2 7b12 8b1}=> 14 Elim r1c123456<>7, r1c123<>8, r2c56<>7, r16c2<>1, r2c5<>6,
{2N234 3N234}+{4r3 6r2 1c2 7c4 78b1}=> 12 Elim r1c1234<>7 , r1c123<>8, r16c2<>1, r49c4<>7, r2c5<>6,
{2N234 3N234}+{4r3 6r2 7r23 18b1} => 9 Elim r1c123<>8 , r1c12<>1 , r2c56<>7, r2c5<>6 , r3c9<>7,
{2N234 3N234}+{4r3 6r2 7r23 1c2 8b1}=> 9 Elim r1c123<>8 , r2c56<>7 , r16c2<>1, r2c5<>6 , r3c9<>7,
D And this 5 cell, rank 1 group , 5 sets {2N23 3N234} + 6 links {6r2 47r3 178b1} => 3 Eliminations r1c123<>8
r3c4 -7- als:(14678)r23c23 -4- r3c4 => r1c123<>8 , rank 1 loop
This one drew my attention (see diagram below) because, however the ALS's are grouped, digits 8 and 1 would be RCDs at the same time (it seems). However, only the 8s in b1 are cleared. I was curious fow ALS rules account for this?
In terms of cover sets (only) 8b1 is rank 0 because of the overlap of cover sets at 7r3c23 (a triplet), thus eliminating the 8s.

- Code: Select all
cover set 8b1 is on the "strong" side of AB triplets
(1b1) (4r3) (6r2) (7r3) (7b1) (8b1)
2N2: 1r2c2=========6r2c2=========7r2c2==8r2c2
| | | |
2N3: | 6r2c3=========7r2c3==8r2c3
| / |
3N3: | 7r3c3B=====8r3c3
| / / |
3N2: 1r3c2==4r3c2===========7r3c2A======8r3c2
| | |
3N4: 4r3c4=========7r3c4 |
r1c123<>8
- Allan Barker
- Posts: 266
- Joined: 20 February 2008
Have you ever seen a naked N-tuple have eliminations different from its complementary hidden M-tuple Have you ever seen a basic row/column N-fish have eliminations different from its complementary M-fish
Have you ever seen a basic row/column N-fish have eliminations different from its complementary M-fish AFAIK the answer to both is "no". Therefore it is reasonable to believe a doubly-linked ALS-xz should have the same eliminations as its hidden set complement.
AFAIK the answer to both is "no". Therefore it is reasonable to believe a doubly-linked ALS-xz should have the same eliminations as its hidden set complement.
ALSs r23c23 and r23c4 have complementary AHSs 3469b1 and 124568b2, respectively. [2 edits: Other complementary AHSs exist as well.]

There are 14 eliminations for this complementary doubly-linked AHS-xz. Since eliminations r6c2<>1 and r49c4<>7 do not exist, I consider these eliminations an "overstatement" for the original ALS-xz.
Of course, no one is going to look at both the ALS-xz and complementary AHS-xz to determine the common eliminations. However, I do expect posters and programmers who claim to be using the ALS-xz to use N cover sets for N base sets, not N+1 cover sets, not N+2 cover sets, etc. (stated as an over-simplification of superposition.)
So what exactly are the consequences of this? For hobiwan's ALS xz above, I would probably select 1b1 and 7b2 to be cover set members, because they have more eliminations than cover sets 1c2 and 7c4, respectively. This merely leaves 1b1\c2 and 7b2\c4 as eliminations for the simpler locked candidates technique.
hobiwan wrote:
- Code: Select all
.--------------------------------.-------------------------.--------------------.
| -1346-7-89 -1346-7-8 6-7-89 | 246-7 146-78 124-7 | 158 157 1578 |
| 2 B1678 B678 | A67 15-6-78 15-7 | 3 4 9 |
| 5 B1478 B78 | A47 3 9 | 2 6 178 |
:--------------------------------+-------------------------+--------------------:
| 13678 9 25678 | 2346-7 467 2347 | 156 12357 12357 |
| 367 23567 4 | 1 67 237 | 9 8 2357 |
| 1367 -12367 267 | 5 9 8 | 16 1237 4 |
:--------------------------------+-------------------------+--------------------:
| 479 457 1 | 8 2 3457 | 45 359 6 |
| 4689 24568 25689 | 349 145 1345 | 7 12359 12358 |
| 4789 24578 3 | 4-79 1457 6 | 1458 1259 1258 |
'--------------------------------'-------------------------'--------------------'
Almost Locked Set XZ-Rule: A=r23c4 {467}, B=r2c23,r3c23 {14678}, X=4,6, Z=6 => r1c12,r6c2<>1, r2c5<>6, r1c123456,r2c56,r49c4<>7, r1c123<>8
ALSs r23c23 and r23c4 have complementary AHSs 3469b1 and 124568b2, respectively. [2 edits: Other complementary AHSs exist as well.]

There are 14 eliminations for this complementary doubly-linked AHS-xz. Since eliminations r6c2<>1 and r49c4<>7 do not exist, I consider these eliminations an "overstatement" for the original ALS-xz.
Of course, no one is going to look at both the ALS-xz and complementary AHS-xz to determine the common eliminations. However, I do expect posters and programmers who claim to be using the ALS-xz to use N cover sets for N base sets, not N+1 cover sets, not N+2 cover sets, etc. (stated as an over-simplification of superposition.)
So what exactly are the consequences of this? For hobiwan's ALS xz above, I would probably select 1b1 and 7b2 to be cover set members, because they have more eliminations than cover sets 1c2 and 7c4, respectively. This merely leaves 1b1\c2 and 7b2\c4 as eliminations for the simpler locked candidates technique.
Last edited by ronk on Wed Apr 15, 2009 9:53 am, edited 2 times in total.
- ronk
- 2012 Supporter
- Posts: 4764
- Joined: 02 November 2005
- Location: Southeastern USA
Paul wrote:Yikes!!! That sounded perilously close to self-serving egotism!!! It's just an attempt to explain where I'm coming from/going to...
Paul, egotism is never self-serving. Your self-consuming drive for discovery is the concentration of a billion years of living evolution onto a single mathematical point that man has now placed on the exemplar pillar of insolvability, called Sudoku, and why the mathematicians had to invent NP complete, in order to warn us. But, we didn't listen.
This is why we are here in this forum.
- Allan Barker
- Posts: 266
- Joined: 20 February 2008
PIsaacson wrote:
I know this sounds confusing if not crazy, but I think we need to consider dual-linked ALSs as a separate entity. Imagine that two ALSs are linked via two RCDs from different nice-loop paths. Then regardless of the distance of separation (path length), as long as they are dual-linked they can provide all the eliminations that would result from the normal dual-linked rules. Replace "nice-loop paths" in the above sentence with "DB bi-value/bi-local stems" or "intermediate ALS chains" and you'll see my point. It doesn't matter how they are dual-linked, it just matters that they are.
I agree with every word of that (well except "confusing and crazy"...)
PIsaacson wrote:Ron,
The stated r3c9<>7 was from the described 6 cells as the base set with the cover set (67r2, 47r3, 1c2, 8b1). I don't understand your reference to "that's for different sets..." (...) My base/cover logic doesn't consider how the base cells were located
All that makes sense to me and I don't follow Ronk's point neither there nor here :
Ronk wrote:There are 14 eliminations for this complementary doubly-linked AHS-xz. Since eliminations r6c2<>1 and r49c4<>7 do not exist, I consider these eliminations an "overstatement" for the original ALS-xz.
which could read like a calling into question of those eliminations.
Labelling dual-linked ALSs as ALS-xz doesn't strike me as a good idea since z in the latter refers to an outside candidate which sees z in both ALSs whereas in dual-linked ALSs z is :
- an outisde candidate which sees
---any non-RCD member of either ALS
---or both of either RCD
- an inside candidate ie member of one ALS which sees all instances of the same candidate in the other set, the so-called cannibalizing situation
=> three z types.
- aran
- Posts: 334
- Joined: 02 March 2007
aran wrote:I don't follow Ronk's point neither there nor here :Ronk wrote:There are 14 eliminations for this complementary doubly-linked AHS-xz. Since eliminations r6c2<>1 and r49c4<>7 do not exist, I consider these eliminations an "overstatement" for the original ALS-xz.
which could read like a calling into question of those eliminations.
Sort of, I suppose. Some of the eliminations cannot occur simultaneously with rank 0 set logic. Specifically, given r23c234 as the base set, I'm saying rank 0 set logic cannot be constructed with both 1b1 and 1c2 in the cover set. Ditto for 7b2 and 7c4.
- ronk
- 2012 Supporter
- Posts: 4764
- Joined: 02 November 2005
- Location: Southeastern USA
PIsaacson wrote:Don,
I know this sounds confusing if not crazy, but I think we need to consider dual-linked ALSs as a separate entity. Imagine that two ALSs are linked via two RCDs from different nice-loop paths. Then regardless of the distance of separation (path length), as long as they are dual-linked they can provide all the eliminations that would result from the normal dual-linked rules. Replace "nice-loop paths" in the above sentence with "DB bi-value/bi-local stems" or "intermediate ALS chains" and you'll see my point. It doesn't matter how they are dual-linked, it just matters that they are.
The above explanation works better for me & I now better understand your point. I agree that dual-linked ALSs are pretty much a separate entity. Just as an aside: Would love to believe that some of these as described above could be found manually.
- DonM
- 2013 Supporter
- Posts: 487
- Joined: 13 January 2008
PIsaacson wrote:I think we need to consider dual-linked ALSs as a separate entity. Imagine that two ALSs are linked via two RCDs from different nice-loop paths. Then regardless of the distance of separation (path length), as long as they are dual-linked they can provide all the eliminations that would result from the normal dual-linked rules. Replace "nice-loop paths" in the above sentence with "DB bi-value/bi-local stems" or "intermediate ALS chains" and you'll see my point. It doesn't matter how they are dual-linked, it just matters that they are.
This all follows directly from set logic. In fact, somewhere I have discussed why rank behaves as a global property independent of logical details, which can seem counterintuitive. Although dual linked ALS have specific properties, the long distance or remote effect is true of virtually all logic that has the same rank and is not specific to these ALS structures.
The unique property of dual linked ALSs (IMO) is that they have equal numbers of base and covers sets, which is also true of continuous nice loops. ALS chains on the other hand have N + 1 cover sets, which is true of discontinuous nice loops. To me, DL-ALSs and CNLs belong in the same category, where as ALS XY*** rules and DNLs belong together. Something link this:
- Code: Select all
Simple links Multi set links (ALS/AHS, etc)
----------------------------------------------------------------------------------------------
Rank 0 Continuous Nice Loops Dual-Link ALS/AHS
Rank 1 Discontinuous Nice Loops ALS/AHS -XZ, chains, etc
Just to expound, an RCD occurs because all the digits of 2 ALS are contained in one cover set, which is like having a rank -1 something. All ALS are rank 1. So 2 ALS + 1 RCD makes a rank 1 chain, 2 ALS + 2 RCDs = rank 0, or, 3 ALS + 3 RCDs = rank 0.
The also applies to logic that is not easily expressible as ALS, like the following alternative to Ronk's 14 elimination AHS above.
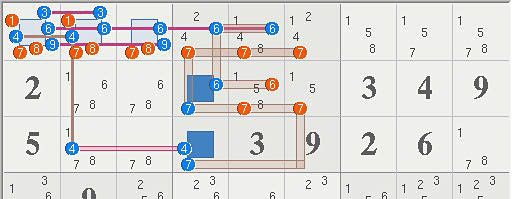
- Allan Barker
- Posts: 266
- Joined: 20 February 2008

