The New Sudoku Players' Forum

[PIsaacson]

Ron,

I wasn't aware of the multi-inference restriction. To be honest, I'm not sure I understand what that even means. But then I've just started investigating Kraken structures, and most of the examples are fish-like patterns so I'm pretty unclear on the hallmark traits of a Kraken deduction right now. I was paying homage to Aran's suggestion

One could then call anything which requires a chain to establish either or both RCDs as a Kraken Dual-linked ALS (in line with use of that term in other contexts).

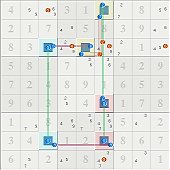
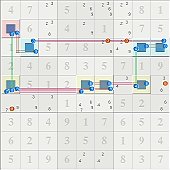
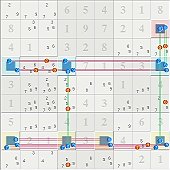
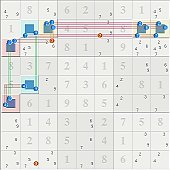
Your re-statement of the ALS chain as a continuous nice-loop is a point that I've conceded before. Although NL discovery is a vastly different process (for me) from ALS chain discovery, once discovered, it really doesn't much matter what you call it or how it was found. The eliminations speak for themselves.

Cheers,
Paul

"What's in a name? That which we call a rose
By any other name would smell as sweet."

[aran]

I had in mind the "tentacular" feature of the fin as in the case of a kraken fish that is : achieving one's purpose by travelling when direct sight is impossible.
This would certainly apply to the second RCD in Paul's example.
However Ronk is saying that Kraken has also a further component : it must occur in a multi-inference context : if the fin is false x is eliminated, if the fin is true, then by a kraken chain x is also eliminated, hence <x>.
Clearly this second component is missing in the RCD context (where this is no "what if/ what if not" situation).
And yet when the fin has direct sight it's not a Kraken fin, so Kraken is intimately linked to travelling.
That might be enough to use it in a dual-linked ALS context where at least one RCD is established by travelling.

[ronk]

I wasn't aware of the multi-inference restriction. To be honest, I'm not sure I understand what that even means. But then I've just started investigating Kraken structures, and most of the examples are fish-like patterns so I'm pretty unclear on the hallmark traits of a Kraken deduction right now.

Usage of the Kraken term has become so pervasive that there may be some exceptions to the multi-inference restriction.

Two easy to understand usages of Kraken are Kraken Cell and Kraken House (row, column, box). A Kraken Cell has three or more candidates. A Kraken House has three or more candidates of the same value. In either case, a simple AIC cannot adequately express the deduction. The complexity must be raised at least to the level of an AAIC.

P.S. The AIC vs AAIC comparison is easier for me than trying to explain multi-inference.

[Allan Barker]

I'm getting murky now, but the chain or structure would have to infer that both RCDs can't be true, right? In other words, weakly linked.

I believe it requires a strong link. But I could be wrong, so don't take me as an authority on this...

I see it as a weak link. If you weakly connect a RCD through a chain, each link of the chain adds 1 truth and 1 new link preserving the rank 0 nature of the logic, so it still works like a DL-ALS. As Ronk mentioned though, I think this winds up as a continuous loop with ALS links.

There are many potential methods of connecting the RCDs and I'm currently debugging several -- almost fish/ERs/AURs are in the works.

Along the same line. The general idea of (rank 0) doubly RCD-linked ALSs can be easily extended to use more ALS and ALS with higher degrees of freedom (rank), such as AALSs. The following rule produces rank 0 logic with eliminations similar to the DL-ALS examples in the thread. The rule is expressed in terms of ALS and RCDs, but can be adapted to other notation or perspecives. With a slight change it would work with hidden logic

A General N Way A*LS Rule – (multi RCD linked), (rank 0)

Count each ALS as 1
Count each AALS counts as 2, etc
Count each independent RCD between 2 ALS, AALS, etc, as 1
Count each independent RCD between 3 ALS, AALS as 2, etc.
Each overlap between 2 RCDs reduces the RCD count by 1.

When the ALS count equals the RCD count, the eliminations proceed as per any normal dual-linked ALS rules.

Although I have checked some structures, a good example is to treat Hobiwan's example here as 3 ALS,

ALS A = r1c45, AALS B=r7c45, AALS C= r9c5

RCD 1 3r79c45 for (BC)
RCD 2 6r79c45 for (BC)
RCD 3 5r17c5 for (AB)
RCD 4 r179c5 for (ABC)

Obviously, this is not required to solve the logic, but it does make a good example.

[DonM]

It appears that there is some confusion over the terms 'doubly-linked' ALSs and 'dual-linked' ALSs. Long, long ago in a far-away galaxy (July 2007), sirdave and I put together the first version of the ALS-Chain tutorial in which we called dual-linked ALSs what ronk calls doubly-linked ALSs. At that time, he suggested that 'doubly' was preferable. When the tutorial was re-written and put on the Player's forum, I changed it to doubly-linked both in deference to ronk whose thread pre-dated the tutorial and also, to not cause confusion.

However, in this thread, the terms dual-linked & doubly-linked are being used apparently interchangeably (though not by ronk ). There was no difference between the 2 terms as far as the structures being described goes in Sept 2007 and afaik, there's still no distinction...unless someone has decided since that there is. I rather liked the term dual and it still seems to trip off the tongue easier than doubly, but ronk's thread was posted first and I think that doubly should be used because now some people are being confused that they are 2 different things.

[PIsaacson]

No one complained about the eliminations in my prior posted (incorrectly titled?) Kraken dual-linked ALS, so I thought I would show a different DL ALS example with the same eliminations, but discovered as a Death Blossom:

The stem cells are the tri-local 4r134c7 with two of the petals the same ALS r2c8 {14} and the other petal ALS b6x289 {1248}. The 2 ALSs are dual-linked with RCDs 14, but what is interesting is that the eliminations for RCD 4 are not restricted to the peers of the two ALSs, but instead restricted to the peers of the ALS and its linking stem cell(s). This is another difference from direct line-of-sight RCDs: The elimination zones for the remotely linked RCDS (substitute whatever term is appropriate for non-direct peered RCDs) depend on how the remote linkage is established. In the case of the 1st ALS, the zone of elimination for RCD 4 is b3 while the zone of elimination for the 2nd ALS and RCD 4 is b6.

I also have a similar DB with stem cells 4r2c5 and 4r4c7 for the same two DL ALSs. The conjugate paired stem cells are the result of x-coloring and I leave it as an exercise in x-coloring to prove that they are truly a conjugate strong-linked pair. But, this reduces the zone of elimination for ALS 1 to 4r2 and omits the r1c9<>4 elimination.

Since the remotely linked RCDs are a box/line GSL in the first DB and an x-cycle in the second, I'm pretty sure that they can be re-stated as continuous nice-loops.

Don,

Just saw your posting regarding dual/doubly linked. If the consensus is doubly, I'll try really hard in the future to type doubly-linked. But I have to opine that dual-linked "sounds" (to my ears at least) more correct. Plus it's easier to type!

Cheers,
Paul

[aran]

No one complained about the eliminations in my prior posted

That's because they were fine

On that structure in your example, my way of looking at it (as in all dual-linked ALS) is
{429} {29} with the RCDs in bold.
Therefore
- anything which eliminates 4 is false : hence <4> r124c9
- anything which eliminates RCD 9 in both ALS is false : zilch
- anything which eliminates RCD 2 in both ALS is false: what is interesting is that each of 2r4c7 and 2r4c9 sees one 2 directly and reaches the other by a little chain. Hence <2> r4c79.
In other words when there is an RCD link established by chain, the RCD type related eliminations will involve a chain (worth remembering).

Since the remotely linked RCDs are a box/line GSL in the first DB and an x-cycle in the second, I'm pretty sure that they can be re-stated as continuous nice-loops

Dual-linked ALS are in fact necessarily expressible as nice-loops.
So you need never wonder about that.

Don,
Just saw your posting regarding dual/doubly linked. If the consensus is doubly, I'll try really hard in the future to type doubly-linked. But I have to opine that dual-linked "sounds" (to my ears at least) more correct. Plus it's easier to type!

Paul
I agree with you on the euphonics, on the typing...in fact given the nature of the debate duel-linked might be even better

[aran]

A General N Way A*LS Rule – (multi RCD linked)
Count each ALS as 1
Count each AALS counts as 2, etc
Count each independent RCD between 2 ALS, AALS, etc, as 1
Count each independent RCD between 3 ALS, AALS as 2, etc.
Each overlap between 2 RCDs reduces the RCD count by 1.
When the ALS count equals the RCD count, the eliminations proceed as per any normal dual-linked ALS rules.

Allan, have you come across a structure with three ALS and three interconnected RCDs ie a count of 3-3=0 eg {abxy} {cdyz} {efzx} where xyz are the RCDs ?
Would be very interesting with potential multiple eliminations :
anything which would eliminate a : false
ditto b, c, d, e, f
anything which would eliminate both x : false
ditto y, z.

[Allan Barker]

Allan, have you come across a structure with three ALS and three interconnected RCDs ie a count of 3-3=0 eg {abxy} {cdyz} {efzx} where xyz are the RCDs ?
Would be very interesting with potential multiple eliminations :
anything which would eliminate a : false
ditto b, c, d, e, f
anything which would eliminate both x : false
ditto y, z.

Yes with some thanks to Paul. These are from one of his databases where I have reconnected the cells. They range from 6 cells to 8 cells but all are connected as 3ALS + 3 RCDs, xy-yz-zx style, or 3-3=0. The 2x2x2 cell example is of course a simple nice loop or perhaps an xy-loop?

Since the general N-Way rule makes rank 0 ALS groups, it has the same kind of eliminations as discussed for the 2 ALS 2 RCD case, and thus all of {a, b, c, d, e, f} and {x, y, z}. (I have clarified the rank 0 point in my last post) The potential eliminations are easy to see in the second group of thumbs, where elimination "zones" (CECs) are shown as yellow candidates.

Thumbs left to right 2x2x2,1x3x4, 1x3x4, 2x2x3
ALS groupings are shown with pale red/blue/yellow cell highlights



Thumbs - with elimination "zones" left to right 2x2x3, 1x2x4
ALS groupings are shown with pale red/blue/yellow cell highlights

[PIsaacson]

Aran,

Not quite what you requested, but an interesting ALS loop that acts like a dual-linked, excuse me, a doubly-linked set in many ways:



My ALS engine claims it's an ALS loop r24c5.<n357> -3- r4c17.<n135> -1- r8c1578.<n13457> with the 1st and last ALSs also linked by an RCD 7, hence a "doubly linked (eXtended)" flagged as an "alsx" with "dualx" tagged eliminations from standard rules.

The full set of 17 eliminations requires (at least for my base/cover code which is less than complete) sub-dividing the complete chain into 2 smaller groupings for some of the eliminations. I don't know if sub-dividing is actually necessary or not, but the 4 base/cover sets I used to find all the flagged eliminations are there for study. I'm still missing assignments, so Xsudo found one additional elimination due to the forced assignment r2c5=5.

Code: Select all

do_alschains - reducing r3c1.<125> by <1> dualx
do_alschains - reducing r9c1.<1235> by <1> dualx
do_alschains - reducing r4c3.<1357> by <3> dualx
do_alschains - reducing r8c9.<359> by <3> dualx
do_alschains - reducing r8c5.<357> by <5> dualx
do_alschains - reducing r8c6.<1579> by <5> dualx
do_alschains - reducing r8c9.<59> by <5> dualx

do_alschains - reducing r4c1.<135> by <3> base/cover
do_alschains - reducing r5c7.<2345> by <5> base/cover
do_alschains - reducing r6c7.<235> by <5> base/cover
do_alschains - reducing r8c1.<135> by <3> base/cover
do_alschains - base/cover {2n5 4n57 8n578} {3r4 34r8 57c5 5c7} -- 6 cell subset

do_alschains - reducing r2c5.<57> by <7> base/cover
do_alschains - reducing r4c3.<157> by <5> base/cover
do_alschains - base/cover {4n157 8n1578} {35r4 345r8 1c1 7c5} -- 7 cell subset

do_alschains - reducing r2c4.<157> by <5> base/cover
do_alschains - reducing r2c6.<157> by <5> base/cover
do_alschains - base/cover {2n5 4n157 8n1578} {5r2 35r4 345r8 1c1 7c5} -- all 8 cells

do_alschains - reducing r3c1.<25> by <5> base/cover
do_alschains - reducing r9c1.<235> by <5> base/cover
do_alschains - base/cover {2n5 4n157 8n1578} {3r4 34r8 15c1 57c5 5c7} -- all 8 cells

do_alschains - alsx[3x5/5] r24c5.<n357> -3- r4c17.<n135> -1- r8c1578.<n13457>

Adding r8c9 to the fray also adds 4 more eliminations: r7c9<>9, r8c6<>9, r9c9<>9 and r4c5<> 5. The nines due to the assignment (now included in the base set) and the five from the missed r2c5=5 assignment.

[ronk]

... an interesting ALS loop that acts like a dual-linked, excuse me, a doubly-linked set ...

re 'doubly':

Bob Hanson (not me) first used the 'doubly' term on his almost-locked sets -- doubly weakly linked thread way back in Dec 2005.

BTW since you're a programmer you must be familiar with some of the works of Donald E. Knuth. Tell me, does he use the term 'doubly-linked list' or 'dual-linked list'?

re 'restricted common candidate' (RCC):

bennys introduced the concepts (and terms) of Almost locked sets xz rule and Almost locked sets xy wing rule back in Nov and Dec of 2005, respectively.

He wrote 'restricted common' and 'common candidate'. He didn't write 'restricted common digit' or even 'common digit'. Since then 'restricted common candidate' (RCC) has stuck for many of us here. But 3 years later you decided here that 'restricted common digit' (RCD) is better, even though AFAICT it means exactly the same thing.

[ronk]

Here is a three ALS deduction that has a little more meat on its bones. [edit: However, this example is not a continuous loop version -- a doubly-linked version -- of an ALS xy-wing.]

Code: Select all

6.9.....8...7.1...4.1.......98.6...4.2.....3..3....5...1.5...7.8...9..........2..

+---------------+-----------------------+------------------------+
| 6    57    9  | 23-4    235-4  235-4  |B(1347) C(1245)   8     |
| 23   58    23 | 7       458    1      | 469     469-5    569   |
| 4    578   1  | 69      2358   69     |B(37)   C(25)     2357  |
+---------------+-----------------------+------------------------+
| 157  9     8  | 123     6      2357   |B(17)   C(12)     4     |
| 157  2     46 | 1489    1457   45789  | 689-17  3        1679  |
| 17   3     46 | 12489   1247   2479   | 5       689-12   12679 |
+---------------+-----------------------+------------------------+
| 239  1     23 | 5       34     3468   | 4689    7        369   |
| 8   A(46)  57 | 123-46  9      237-46 |B(1346) C(1456)   135-6 |
| 39   46    57 | 13468   1347   34678  | 2       4689-15  13569 |
+---------------+-----------------------+------------------------+

TP13 26 Candidates, Raw Rank = 0 (linksets - sets)
     9 Sets = {8N2 1348N7 1348N8}
     9 Links = {4r18 6r8 137c7 125c8}
     15 Eliminations -->
     r1c456<>4, r8c469<>6, r8c46<>4, r69c8<>1, r29c8<>5, r5c7<>17, r6c8<>2

There is another rank 0 cover set {4r8 6r8 137c7 125c8 4b3} for added eliminations r2c78<>4.

When viewed as three ALSs, the ALSs are r8c2 (A), r1348c7 (B) and r1348c8 (C). Note that A is doubly-linked to both B and C. [edit: However, as noted above, this example is not a doubly-linked ALS xy-wing.]

When viewed as one AALS and two ALSs, the AALS is r8c278 ... and the two ALSs are r134c7 and r134c8. This would (I think) normally yield three RCCs for the AALS, but for some reason there are four here, with candidate <1> being repeated.

[Allan Barker]

When viewed as one AALS and two ALSs, the AALS is r8c278 ... and the two ALSs are r134c7 and r134c8. This would (I think) normally yield three RCCs for the AALS, but for some reason there are four here, with candidate <1> being repeated.

Nice catch and observation. The reason for the apparent extra RCC is:

Neither RCC (1)c7 or (1)c8 is an RCC by itself, at least when RCCs are defined as digits that cannot appear (be true) in 2 A*LS at the same time. However, RCC 1c7 and 1c8 combined do the job of a single RCC. This can be described a couple of ways.

1. The 2 combined RCCs prevent the digit 1 from appearing in all 3 A*LS at the same time, or.
2. The 2 combined RCCs are able to cover the digit 1 in all three A*LS.

The N-Way rule above is still correct but would require an additional rule for redundant RCCs to cover this case.

[DonM]

Further thoughts on terminology (since it is raised above): My view is that the best terminology is that which both causes the least confusion and is the most descriptive. Sometimes there is a collision between both goals. Thus, the doubly-linked thread has been around long enough such that introducing another term would cause, and already has caused, confusion, but in addition to that, 'doubly' does appropriately describe the structure (even though, as I've said, I like the sound of 'dual' better).

The term Kraken is another matter. Much as I like the originator of the term, my guess is that it has caused a lot of confusion because it has been applied to all sorts of structures that have no relationship to each other. How would someone trying to learn advanced solving possibly figure this out on their own. The term Kraken was first used to apply to the multi-inference Kraken/cell,row,column (what I prefer to call AAICs because its more descriptive), but very soon after, circa Aug-Sept 2006, was applied to various other entities, some of which are far 'simpler' than multi-inferences, but which, now given the Kraken moniker, imply complexity.

Take the Kraken fish: It's nothing more than a structure whereby an x-wing fin 'sees' the typical x-wing cec(s) thru a conjugate link. Either the x-wing being true or the fin being true will kill the target candidates. There must be a better name for this: Conjugate Finned X-wing? . But it's too late for that methinks. In any event, IMO, the preferred terminology for any future 'new' structures should be, as much as possible, descriptive of the structure for the benefit of the poor new solver trying to figure all these terms out.

[PIsaacson]

Note that A is doubly-linked to both B and C.

I don't see how candidate 4 in A qualifies as an RCC peer of all the 4s in either B or C? But a really interesting set of ALSs regardless of how they are linked.