The New Sudoku Players' Forum

by **champagne** » Sun Nov 30, 2008 11:44 pm

Hi,
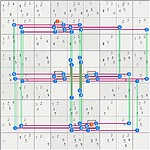
Working on Allan model, I had the feeling that some specific patterns, close or belonging to the fishes family, could play a key role.

I was missing an example to open the discussion.

tarx0075 starts gives me an opportunity to do it. I doubt this is new, but I have no time to dig in all posts written on fishes. Anyway, applying it to Allan model lead to a wider scope, although most often, we will have pure “almost fishes”

Let’s start with tarx0075 example

Code: Select all: ........6..5..18...9...8.7....8.2.....3.1.2..4..5.3....6.....9...83..1..7.......4#tarx0075 1238 123478 1247 |2479 234579 4579 |3459 12345 6 236 2347 5 |24679 234679 1 |8 234 239 1236 9 1246 |246 23456 8 |345 7 1235 --------------------------------------------------------- 1569 157 1679 |8 4679 2 |345679 13456 13579 5689 578 3 |4679 1 4679 |2 4568 5789 4 1278 12679 |5 679 3 |679 168 1789 --------------------------------------------------------- 1235 6 124 |1247 24578 457 |357 9 23578 259 245 8 |3 245679 45679 |1 256 257 7 1235 129 |1269 25689 569 |356 23568 4

We will work exclusively on digits 4679, column 3467 and box 5.
I reduce the PM to that map focusing on used positions

Code: Select all: 47+ |479+ o 479+ |49+ - |4679+ o - |- 46+ |46+ o - |4+ ------------------------------ 679+ |- 4679 - |4679+ - |4679 - 4679 |- 679+ |- 679 - |679 ------------------------------- 4+ |47+ o 47+ |7+ - |- o 4679+ |- 9+ |69+ o 69+ |6+

All cells with given ‘-‘
Unused cells ‘o’
Extra candidates ‘+’.

Next point what if ‘4’;’6’;’7’;’9’ is in cells r46c5.
We will consider each digit independently and conclude at the end.

1)4r4c5 => B5 and r4 occupied.
Here after the diagram for columns 3467

Code: Select all: N24 N86 4R1 4R3 4R7 | | | | | 4c7 417 437 | 4c3 413 433 473 4c6 | 486 416 436 4c4 424 | 414 434 474

This diagram is shown following Allan Barker representation with “sets” in horizontal and “Link sets” in vertical. No missing candidate in horizontal, but some in vertical.

In that pattern, 4r2c4 + 4r8c6 false lead to a deadly pattern(locked fish four columns within three lines).

One at least of 4r2c4;4r8c6 must be true.

2)6r46c5 to clarify, I split in 2 cases 6r4c5 and 6r6c5

Code: Select all: N24 N86 6R6 6R3 6R9 assuming 6r4c5 | | | | | 6c4 624 | 634 694 6c6 | 686 =|===|==696 6c3 | 663 633 6c7 | 667==|==697 N24 N86 6R4 6R3 6R9 assuming 6r6c5 | | | | | 6c4 624 | 634 694 6c6 | 686 =|===|==696 6c3 | 643 633 6c7 | 647==|==697

Same sub patterns as before, must have at least one of 6r2c4;6r8c6

3)7r46c5 split in 2 sub patterns

Code: Select all: N24 N86 7R6 7R1 7R7 assuming 4r4c5 | | | | | 7c4 724 | | 714 774 7c6 | 786 | 716 776 7c3 | | 763 713 7c7 | | 767 777 N24 N86 7R4 7R1 7R7 assuming 7r6c5 | | | | | 7c4 724 | | 714 774 7c6 | 786 | 716 776 7c3 | | =743 713 7c7 | | =747 777

Same pattern, must be one at least of 7r2c4;7r8c6

4)9r46c5 split in 2 sub patterns

Code: Select all: N24 N86 9R6 9R1 9R9 assuming 9r4c5 9c4 924 | | 914 994 9c6 986 | 916 996 9c3 ======= 963 | 993 9c7 ======= 967 917 N24 N86 9R4 9R1 9R9 assuming 9r6c5 9c4 924 | | 914 994 9c6 986 | 916 996 9c3 ======= 943 | 993 9c7 ======= 947 917

Again same pattern and the conclusion:

Whatever is the couple of digits solving r46c5, the 2 same digits will solve r2c4;r8c6.

This gives for sure r2c4<>2 and r8c<>6, but also a significant step in the six possible scenarios

4&6 r46c5 => 4&6 r2c4r8c6
4&7 r46c5 => 4&7 r2c4r8c6
. . .
7&9 r46c5 => 7&9 r2c4r8c6

Generalized “Almost fishes patterns”

That example uses only one pattern. This is a wide field to explore. I like to use Allan representation sets / link sets to open the topic.

Here examples of possible patterns. S1…Sn are sets as defined in Allan model (row, column, box or Cell/Node. We already know that one can mix boxes and rows/columns in a fish pattern. I don’t know if mixing cells/Node with rows, columns, boxes is realistic.

Code: Select all: L1 L2 L3 L4 + + + ( Y ) S1 . . . S2 . . . S3 x . . . X => Y #X => #Y several interesting patterns like in URs

Code: Select all: L0 L1 L2 L3 L4 + + + S1 . . . S2 . . . S3 X . . . S4 Y . . . X or Y and again, several sub patterns.

Surely other suggestions should come.

What is for sure is that you can bring in AIC’s such binary conditions as it has been done with UR’s.

champagne

by **ronk** » Mon Dec 01, 2008 1:26 am

While studying Allan Barker's post here, I noticed the structure could be viewed as four finned franken starfish with overlapping base sets -- (4679)c3467b5. Since there is no "cell unit" in fish, b5 is a logical choice for the 5th base set.

Unfortunately, I've been unable to reason it all the way through to the known deductions, so I can only present my fish diagrams with a few comments.

Code: Select all: four overlapping finned franken starfish at the start of tarx0075 . . 4 | 4 . 4 | 4 . . <-- . . / | / . / | / . . . . / | #4 . / | / . . . . / | #6 . . | . . . . . 4 | 4 . x | 4 . . <-- . . 6 | 6 . x | x . . <-- cover sets ---------+----------+---------- ---------+----------+---------- . . x | / 4 / | 4 . . <-- . . 6 | / 6 / | 6 . . <-- . . / | @4 / @4 | / . . <-- . . / | @6 / @6 | / . . <-- . . / | / / / | / . . . . 6 | / 6 / | 6 . . <-- ---------+----------+---------- ---------+----------+---------- . . 4 | 4 . 4 | x . . <-- . . / | / . / | / . . . . / | / . #4 | / . . . . / | / . #6 | / . . . . / | / . / | / . . . . x | 6 . 6 | 6 . . <-- (4)c3467b5\r13457 + fins r2c4,r8c6 (6)c3467b5\r34569 + fins r2c4,r8c6 . . 7 | 7 . 7 | x . . <-- . . x | 9 . 9 | 9 . . <-- . . / | #7 . / | / . . . . / | #9 . / | / . . . . / | / . / | / . . . . / | / . / | / . . ---------+----------+---------- ---------+----------+---------- . . 7 | / 7 / | 7 . . <-- . . 9 | / 9 / | 9 . . <-- . . / | @7 / @7 | / . . <-- . . / | @9 / @9 | / . . <-- . . 7 | / 7 / | 7 . . <-- . . 9 | / 9 / | 9 . . <-- ---------+----------+---------- ---------+----------+---------- . . x | 7 . 7 | 7 . . <-- . . / | / . / | / . . . . / | / . #7 | / . . . . / | / . #9 | / . . . . / | / . / | / . . . . 9 | 9 . 9 | x . . <-- (7)c3467b5\r14567 + fins r2c4,r8c6 (9)c3467b5\r14569 + fins r2c4,r8c6 KEY: / - cells which must be void of the respective candidate x - cells which need not be void of the respective candidate # - (normal) fins, i.e., candidates which are not covered by the 5 indicated cover sets @ - endo-fins, i.e., the the cells are members of two base sets

First note that all four starfish share fin and endo-fin cells. Because of the endo-fins, it seems reasonable that r5 should be the common 5th cover unit for the 5x5 basic starfish. This leaves shared fin cells r2c4 and r8c6 uncovered.

r5c46 contains only digits 4679, i.e., r5c4 and r5c6 can contain only two of the four digits. Therefore, at least two of the four starfish cannot exist. To paraphrase Allan, the question remains: How to prove that the other two fin cell locations, r2c4 and r8c6, must contain the remaining two digits :?:

This is equivalent to proving that none of the four starfish can exist. Unfortunately, that's where I'm stuck, so close and yet so far, I think.

[edits: 1) minor text touchups; 2) 4r6c5 was shown as req'd void; 3) undid edit2]

by **champagne** » Mon Dec 01, 2008 1:36 am

ronk wrote:While studying Allan Barker's post here, I noticed the structure could be viewed as four finned franken starfish with overlapping base sets -- (4679)c3467b5. Since there is no "cell unit" in fish, b5 is a logical choice for the 5th base set.

Unfortunately, I haven't yet reasoned it all the way through to the known deductions, so I'll just present my diagrams with a few comments.
....
Unfortunately, that's where I'm stuck, so close and yet so far, I think!

First of all, we have exactly the same situation.

The way to prove it is what I just posted.

Any 4,6,7,9 in any of the cells r4c5;r5c6 forces one of the two cells r2c4;r8c6 filled with that digit.

It is enough. May be you don't like splitting the problem :?:

I have no equivalence in AIC's

champagne

by **ronk** » Mon Dec 01, 2008 2:24 am

champagne wrote:The way to prove it is what I just posted.

It is enough. May be you don't like splitting the problem

Correct, if by "splitting" you mean your "cases". I was hoping for a more direct and intuitive argument. But then ... you actually have a proof, and I don't.

champagne wrote:I have no equivalence in AIC's

I think it is unreasonable to expect all deductions made by constraint-set theory to be expressible with chains.

by **champagne** » Mon Dec 01, 2008 2:48 am

ronk wrote:Correct, if by "splitting" you mean your "cases". I was hoping for a more direct and intuitive argument. But then ... you actually have a proof, and I don't.

I faced the same problem as you when I had the feeling that deadly patterns on fishes should work.

Nothing came.

Reading Allan comments and analyzing my own way to to find the rank 0 part of the diagram, I came to the conclusion that in any way you had to split the problem. Here, the overall situation is complex, I hope a direct conclusion will be possible in easier cases.

by **ronk** » Mon Dec 01, 2008 4:37 am

champagne wrote:
ronk wrote:Correct, if by "splitting" you mean your "cases". I was hoping for a more direct and intuitive argument. But then ... you actually have a proof, and I don't.

I faced the same problem as you when I had the feeling that deadly patterns on fishes should work.

Thanks, that's the hint I needed.

Once two of the four digits occupy r5c46, r5 is no longer an effective cover set for the remaining two starfish, which then have five base sets and four cover sets. Because these last two starfish cannot then exist, the two shared fin cells r2c4 and r8c6 must hold the remaining two digits.

champagne wrote:Reading Allan comments and analyzing my own way to to find the rank 0 part of the diagram, I came to the conclusion that in any way you had to split the problem. Here, the overall situation is complex, I hope a direct conclusion will be possible in easier cases.

I agree that "splitting the problem" is in all likelihood required. However, judging from what I've seen Allan Barker post, I think this is one of the "easier cases."

by **Allan Barker** » Mon Dec 01, 2008 5:04 am

Ronk wrote:While studying Allan Barker's post here, I noticed the structure could be viewed as four finned franken starfish with overlapping base sets -- (4679)c3467b5. Since there is no "cell unit" in fish, b5 is a logical choice for the 5th base set.

I just happen to have one of those (I think) in the batch of 6 different logic layouts I mentioned in the other thread. It is the only example I found that does not have cell base sets. Does this one match your proposal?

There are only the 4 vertical cell cover sets in 2n4, 5n46, and 8n6, the positions of your 4 fins. I think this is about the same.

The only thing of note might be the 4 cell cover sets are all rank 0.

Thumbs. Note: Rank 0 cell base sets are in black.

Tarx0075 Initial Loop A, all base sets in layers

Code: Select all: E75A 47 Nodes, Raw Rank = 0 (linksets - sets) 16 Sets = {4679r2 4679r5 4679r8 4679b5} 16 Links = {69c1 47c2 4679c5 46c8 79c9 25n4 58n6} --> (2n4) => r2c4<>2, (8n6) => r8c6<>5 +--------------------------------------------------------------------------------------+ | 1238 123478 1247 | 2479 234579 4579 | 3459 12345 6 | | 23(6) 23(47) 5 | 2(4679) 23(4679) 1 | 8 23(4) 23(9) | | 1236 9 1246 | 246 23456 8 | 345 7 1235 | +--------------------------------------------------------------------------------------+ | 1569 157 1679 | 8 (4679) 2 | 345679 13456 13579 | | 58(69) 58(7) 3 | (4679) 1 (4679) | 2 58(46) 58(79) | | 4 1278 12679 | 5 (679) 3 | 679 168 1789 | +--------------------------------------------------------------------------------------+ | 1235 6 124 | 1247 24578 457 | 357 9 23578 | | 25(9) 25(4) 8 | 3 25(4679) 5(4679) | 1 25(6) 25(7) | | 7 1235 129 | 1269 25689 569 | 356 23568 4 | +--------------------------------------------------------------------------------------+ Logic Diagram - no eliminations shown 2n4 4c2 4c5 4c8 6c5 6c1 6c8 5n6 5n4 7c5 7c2 7c9 8n6 9c5 9c9 9c1 4R8: 482==485===============================================486 | | | 4B5: | 445======================456E=454A | | | | | | 4R5: | | 458=================456E=454A | | | | | | | 4R2: 424==422==425==428 | | | | | | | 6R8: | 685=======688===|====|==================686 | | | | | | 6R2: 624=================625==621 | | | | | | | | | | | 6R5: | | 651==658==656F=654B | | | | | | 6B5: | 645============656F=654B | | 665 | | | | | | | 7R8: | | | 785=======789==786 | | | | | | 7R2: 724=================================|====|===725==722 | | | | | | | | | 7B5: | 756G=754C=745 | | | | | | 765 | | | | | | | | | 7R5: | 756G=754C======752==759 | | | | | 9R8: | | | 986==985=======981 | | | | | 9R2: 924=================================|====|=======================925==929 | | | | | | 9B5: 956H=954D=====================945 | | | | 965 | | | | | | 9R5: 956H=954D==========================959==951 === base set --- cover set A, B, C, ... designates same candidate in 2 or more sets

by **champagne** » Mon Dec 01, 2008 5:50 am

Hi Allan,

I thought a while that one would be easier to handle (showing more opacity towards the topic I introduced here).

16 sets 16 linksets global rank 0.

Unfortunately, I discovered quickly triple points sets form . I guess at the end we will have the same kind of problems as in the previous diagram.

This new diagram reinforce my intimate conviction that many solutions can come out in such complex combinations of floors. My solver will produce one among others, (trying to put as much symmetry as possible).

Nice work

champagne

by **ronk** » Mon Dec 01, 2008 6:08 am

Allan Barker wrote:
Ronk wrote:While studying Allan Barker's post here, I noticed the structure could be viewed as four finned franken starfish with overlapping base sets -- (4679)c3467b5. Since there is no "cell unit" in fish, b5 is a logical choice for the 5th base set.

I just happen to have one of those (I think) in the batch of 6 different logic layouts I mentioned in the other thread. It is the only example I found that does not have cell base sets. Does this one match your proposal?

There are only the 4 vertical cell cover sets in 2n4, 5n46, and 8n6, the positions of your 4 fins. I think this is about the same.

I'm reasonably sure it is. Since it's the smaller jellyfish and requires a few less empty cells (voids), I would normally say it's preferable to the starfish POV.

However, I don't see an easy verbal argument justifying the eliminations, as for the starfish above.

Allan Barker wrote:The only thing of note might be the 4 cell cover sets are all rank 0.

With triple points at r5c46, I don't think I'll ever understand this.

by **ronk** » Mon Dec 01, 2008 5:07 pm

champagne and Allan Barker,

If candidate 4 existed at r6c5 in tarx0075, would your methods still yield the eliminations in r2c4 and r8c6? IOW are the eliminations dependent upon candidate 4 being missing at r6c5 :?:

by **Allan Barker** » Mon Dec 01, 2008 9:21 pm

Ronk wrote:I'm reasonably sure it is. Since it's the smaller jellyfish and requires a few less empty cells (voids), I would normally say it's preferable to the starfish POV.

When I saw your theoretically proposed logic was so similar to something I had seen, I didn't stop to notice that my pattern was the row equivalent of your's. Otherwise the logic looks the same.

Champagne wrote:I thought a while that one would be easier to handle (showing more opacity towards the topic I introduced here).
<<16 sets 16 linksets global rank 0.>>
Unfortunately, I discovered quickly triple points sets form.

Ronk wrote:However, I don't see an easy verbal argument justifying the eliminations, as for the starfish above.

Arguments based on rank and triplets can be quite difficult for complex structures like this. It would be nice if layered fish approaches eventually provide something more practical.

However, a rank argument would use the base-set triplet rule.

A base-set triplet can raise the rank by 1, but not in its (upper) cover-set branch. The upper branch usually extends until there are two independent return paths to the other two branches. It is defined by a cover-set region derived by assuming the triplet is occupied.

1) Your logic (all layers) has equal numbers of base and cover sets and would be rank 0 without triplets.
2) At any time, 2 exo-fins (triplets) must be occupied. This raises the rank inside the 2 occupied layers, but not in the direction of the triplets' upper branches, 5n46, or the other layers.
3) Thus, the 2 other layers will be rank 0, including cover-sets 2n4 and 8n6, which cause the eliminations.
4) None of the layers can always be 0, thus only the 4 cell cover-sets are guaranteed to be rank 0.
.

by **Allan Barker** » Mon Dec 01, 2008 9:49 pm

ronk wrote:champagne and Allan Barker,
If candidate 4 existed at r6c5 in tarx0075, would your methods still yield the eliminations in r2c4 and r8c6? IOW are the eliminations dependent upon candidate 4 being missing at r6c5

The full answer is....

20 set column base-set Starfish type,

No elimination, because 4r6c5 requires an additional cover-set dropping the global (raw) rank 1.

16 set row base-set Swordfish type,

Yes, elimination, because 4r6c5 is covered by an existing column cover-set so the global (raw) rank is still 0.

I tested both options in my "analyzer" to confirm.

by **champagne** » Mon Dec 01, 2008 10:09 pm

ronk wrote:champagne and Allan Barker,

If candidate 4 existed at r6c5 in tarx0075, would your methods still yield the eliminations in r2c4 and r8c6? IOW are the eliminations dependent upon candidate 4 being missing at r6c5

I red Allan Answer. Let me tell it differently.

4r6c5 can not be. We have already 4r6c1 given

More seriously, this can explain the slightly different role played by '4'.

If I look at the 4th floor, it seems to me that "guessing" 4r6c5 true does not give a nice picture. The reason is that no row disappears. If none of the 2 targets is true, then you have a valid pure fish

I did not look after other diagrams.

champagne;

by **champagne** » Tue Dec 02, 2008 2:21 am

Hi ronk,

Another way to answer your point, and another picture for that topic.

Here is the position for 6r46c5, keeping the sets in horizontal.

Code: Select all: r2 r8 r3 r4 r6 r9 c3 6 6 6 c4 6 6 6 c5 6 6 c6 6 6 c7 6 6 6

Here again, if you assume r2c4 an r8c6 false, you have a deadly pattern.

My split in 2 cases was not necessary. We just skip from an "almost" swordfish to an "almost" Jellyfish.

champagne

by **ronk** » Tue Dec 02, 2008 2:37 am

champagne wrote:
Code: Select all
r2 r8 r3 r4 r6 r9 c3 6 6 6 c4 6 6 6 c5 6 6 c6 6 6 c7 6 6 6

Here again, if you assume r2c4 an r8c6 false, you have a deadly pattern.

How can you ignore the other digit 6 candidates in c5? Did you mean b5?

Looks much the same as my verbal argument, where I wrote: Because these last two starfish cannot then exist, the two shared fin cells r2c4 and r8c6 must hold the remaining two digits.

champagne wrote:My split in 2 cases was not necessary. We just skip from an "almost" swordfish to an "almost" Jellyfish.

I don't see anything as small as a swordfish here, [edit: but it may be because I don't know what you mean by "almost" fish. For me, they're just finned fish, both sashimi and non-sashimi.]

The New Sudoku Players' Forum

Almost Fishes patterns

Almost Fishes patterns