The New Sudoku Players' Forum

by **Allan Barker** » Wed Dec 03, 2008 6:09 am

Champagne wrote:Nice findings with theses starts, but I would like to share some experiences and perplexity.
In tarx0075, first assigned following Allan model is 2r6c2.
I introduced it as given and processed the puzzle in my standard way.
Results were [worse] than without that given. Likely this new given opened new doors, but did not simplify the main path.

I agree, and I think this is also true for most methods. For the really difficult puzzles, these loops are just a small appetizer, they may not help solve the puzzle at all.

Champagne wrote:..... these 2 eliminations don't come in the first ten of my process.

This is the only significant difference I see, these loop-like structures often come first when searching for base/cover set elimination logic. I don't know why.

Champagne wrote:.It seems that both ways (Allan Model and AIC's nets) are fighting against completely different weaknesses of the puzzle.

Maybe this is also becasue one is base/cover set based, and another is AIC based?

What do you think about non symetrical floors??

by **champagne** » Wed Dec 03, 2008 6:35 am

Allan Barker wrote:1)I agree, and I think this is also true for most methods. For the really difficult puzzles, these loops are just a small appetizer, they may not help solve the puzzle at all.

2)What do you think about non symetrical floors??

1) I would not be as negative as you. Fata Morgana as been 100% solved by you and nothing came up to now with my AIC's;

2) If GN is for you an example of "non symmetric puzzle", I see no difference. The first elimination we have 3r7c9, is far away in my solution.

champagne

by **ronk** » Thu Jan 01, 2009 5:11 am

For Silver Plate, champagne wrote:using floors 1357 you can only eliminate 8r5c2 and 2r4c8

using floors 13457 your can eliminate 1r3c9 4r7c2 plus 8r5c2 and 2r4c8

using floors 13678 you can eliminate 1r6c9 7r3c6 8r5c2

This is a month old, but would you please provide details for the last two? Specifically, in which units (rows, cols, boxes) are those "floors" applied? I can probably take it from there.

by **champagne** » Thu Jan 01, 2009 7:14 am

ronk wrote:
For Silver Plate, champagne wrote:using floors 1357 you can only eliminate 8r5c2 and 2r4c8

using floors 13457 your can eliminate 1r3c9 4r7c2 plus 8r5c2 and 2r4c8

using floors 13678 you can eliminate 1r6c9 7r3c6 8r5c2

This is a month old, but would you please provide details for the last two? Specifically, in which units (rows, cols, boxes) are those "floors" applied? I can probably take it from there.

Hi ronk,

When I investigated eliminations possibilities in Silver Plate, I did not try to find a "SLG" which is likely what you are looking for.

I need some time, may be one or two days to do it.

champagne

by **champagne** » Thu Jan 01, 2009 10:28 pm

ronk wrote:
For Silver Plate, champagne wrote:using floors 1357 you can only eliminate 8r5c2 and 2r4c8

using floors 13457 your can eliminate 1r3c9 4r7c2 plus 8r5c2 and 2r4c8

using floors 13678 you can eliminate 1r6c9 7r3c6 8r5c2

This is a month old, but would you please provide details for the last two? Specifically, in which units (rows, cols, boxes) are those "floors" applied?
I can probably take it from there.

Hi ronk,
I investigated slightly more on that puzzle. The first step is quite "standard" if we refer to what has been seen in "Fata Morgana".

Code: Select all: 1 458 4689 |3568 23589 35689 |2349 239 7 589 2 789 |4 135789 35789 |139 6 189 4689 478 3 |1678 12789 6789 |5 129 12489 --------------------------------------------------------- 23568 9 12678 |13578 4 3578 |12367 12357 1256 358 13578 178 |13578 6 2 |1379 4 159 23456 13457 12467 |9 1357 357 |8 12357 1256 --------------------------------------------------------- 2489 148 5 |678 789 46789 |124679 1279 3 349 6 149 |2 3579 34579 |1479 8 1459 7 348 2489 |3568 3589 1 |2469 259 24569

If we consider r6c56, the Allan model says that whatever is the solution for r6c56, r4c8;r5c2 has a solution within 1,3,5,7.

I am ready to bet that 1r6c56 => 1r4c8r5c2 . . . but it has to be established.

The smallest group proposed by the solver is the following (35 sets)

Code: Select all: N:......... ......... ......... ......... ......... ....XX... ......... ......... ......... R:..X..XX.. ......... .X.XXX..X ......... X....X..X ......... .X.XX..X. ......... ......... C:.X..X..X. ......... XX.X..X.. ......... .X.X...X. ......... ..X.XXX.. ......... ......... B:.X....... ......... .X..X.... ......... ....X.... ......... ......... ......... ......... 1 2 3 4 5 6 7 8 9 NE......... ......... ......... .......X. .X....... ......... ......... ......... .........

It should be possible to establish the expected property based on that group.

I guess trying to work directly on cases 2 and 3 would be disappointing.
The way my solver works is to eliminate first 8r5c2 and 2r4c8, then to look for another elimination using Allan model.

Code: Select all: 1 458 4689 |3568 23589 35689 |2349 239 7 589 2 789 |4 135789 35789 |139 6 189 4689 478 3 |1678 12789 6789 |5 129 12489 --------------------------------------------------------- 23568 9 12678 |13578 4 3578 |12367 1357 1256 358 1357 178 |13578 6 2 |1379 4 159 23456 13457 12467 |9 1357 357 |8 12357 1256 --------------------------------------------------------- 2489 148 5 |678 789 46789 |124679 1279 3 349 6 149 |2 3579 34579 |1479 8 1459 7 348 2489 |3568 3589 1 |2469 259 24569

next to come is potential elimination of 1r3c9 4r7c2 using floors 13457

the minimum group found by the solver is that one (55 sets)

Code: Select all: N:......... ......... ......... ......... ......... ....XX... ......... ......... ......... R:..XXXXX.. ......... .X.XXX.X. ..X...X.. XX...X..X ......... .XXXXXXX. ......... ......... C:.X.XX..X. ......... XX..XXX.. .X...X... XX.XXX.X. ......... ..XXXXX.. ......... ......... B:...X..... ......... ...XX.... X........ ...XX.... ......... ...XX.... ......... ......... 1 2 3 4 5 6 7 8 9

Looking for smaller groups, the solver finds a possibility to eliminate 4r7c2 using 39 sets

Code: Select all: N:......... ......... ......... ......... ......... ....XX... ......... ......... ......... R:.....X... ......... .X.XXX.X. ......X.. XX...X..X ......... .X.XXX.X. ......... ......... C:.X....... ......... X...XXX.. .....X... XX.XXX.X. ......... ..X.X.X.. ......... ......... B:......... ......... ...XX.... ......... ...XX.... ......... ...XX.... ......... ......... 1 2 3 4 5 6 7 8 9

Only two sets for digts '1' and '4'. The corresponding diagram should be relatively easy to analyze

Reversely, elimination of 1r3c9 (not considering elimination of 4r7c2 done) requested a group of 52 sets

Code: Select all: N:......... ......... ......... ......... ......... .....X... ......... ......... ......... R:..XXXXX.. ......... .X.XXX.X. ..X...... XX...X..X ......... .XXXXXXX. ......... ......... C:.X.XX..X. ......... XX..XXX.. .X....... XX.XXX.X. ......... ..XXXXX.. ......... ......... B:...X..... ......... ...XX.... X........ ...XX.... ......... ...XX.... ......... ......... 1 2 3 4 5 6 7 8 9

nearly all the group necessary for both.

I hope this will give you the clues your are waiting for. This is what I can get without modifying the program.

Allan would likely do a beter work starting from that.

champagne

by **champagne** » Thu Jan 01, 2009 11:02 pm

Hi,

A player pushed me to work on the last version of Allan Barker first loop for Golden Nugget.

Code: Select all: 1c7 2c7 1c2 1b1 2c1 1c4 2c4 7n9 3n9 3n8 2n8 4n8 4c6 7c1 4c2 7c6 4c7 7c7 1R1: 117=======112A=112A | | 113 } | | | } 1R3: | 132B=132B=====================139==138 } | | | | } SIS 1 1R7: 177=======172============174=======179 | | } | | | | | } 1R4: 147======================144========|====|====|========148 } | | | | 2B3: 217============================|===239F=238C=228 | } 227 | | | | | } | | | | | | } 2R7: 277======================274==279 | | | | } SIS 2 | | | | | | | } 2R3: | 231=======234===|===239F=238C | | } | | | | | | | } 2R4: 247============241=============|====|====|====|===248 } | | | | | 6C8: | | 638==628 | } SIS 3 | | | | | 4B3: { | 439G=438D=428===|=======================417 { | | | | | 427 { | | | | | | 4R4: SIS 4 { | | | | 448============442=======447 { | | | | | | | 4R3: { | 439G=438D==|====|===436=======432 | { | | | | | | | 4R7: { 479===|====|====|====|===476=================477 | | | | | 7B3: { | 739H=738E=728===|============================717 { | | | | 727 { | | | | | 7R4: SIS 5 { | | | 748=================746=======747 { | | | | | 7R3: { | 739H=738E================731=======736 | { | | | 7R7: { 779===========================771=================777

Code: Select all: +--------------------------------------------------------------------------------------+ | 25678 4568(1) 24567(1) | 268 2467 4678 | (1247) 3 9 | | 26789 4689 2467 | 23689 23467 1 | (247) (2467) 5 | | 69(27) 69(14) 3 | 69(2) 5 69(47) | 8 (12467) (1247) | +--------------------------------------------------------------------------------------+ | 35(2) 35(4) 8 | 35(1) 9 35(7) | 35(1247) (1247) 6 | | 3569 7 456 | 13568 136 2 | 13459 1489 1348 | | 1 3569 256 | 4 367 35678 | 23579 2789 2378 | +--------------------------------------------------------------------------------------+ | 36(7) 36(1) 9 | 36(12) 8 36(4) | 3(1247) 5 -3(1247) | | 3578 2 157 | 1359 134 3459 | 6 14789 13478 | | 4 13568 156 | 7 1236 3569 | 1239 1289 1238 | +--------------------------------------------------------------------------------------+

This is an interesting picture, somehow similar to some proposed ways to explain the Fata Morgana and tarx0075 first loop.

We will first note that floor '6' has a very limited use.

My preferred translation is that r2c8r3c89 is an AAHS/AC2 ('6 compulsory).

This AC2 has six 'super candidatee' 1&2 1&4 1&7 2&4 2&7 4&7
It behaves like a dual cell object.

If you study carefully that diagram you will see that

1 not in r2c8r3c89 => 1 in r4c8r7c9
same with '2','4','7'

All of them lead to deadly fish pattern if r2c8r3c89 is not valid

exactly the situation described by ronk in tarx 0075 with cells r2c4 r5c46 r8c6.

Whatever is the super candidate solving r4c8r7c9, r2c4r8c6 is occupied by the two complementary digits.

champagne

ps: I did not check all posts, I apologize in advance in case this would be redundant.

EDIT: if instead of r2c8r3c89 'off' you use r12c7 'on', you have the other way to show the same reality.

Edit 2 missed the name of the puzzle to Golden Nugget added
also reference to tarek 0075 changed
sorry ronk

by **ronk** » Fri Jan 02, 2009 2:45 am

champagne wrote:A player pushed me to work on the last version of Allan Barker first loop.
Code: Select all
+--------------------------------------------------------------------------------------+ | 25678 4568(1) 24567(1) | 268 2467 4678 | (1247) 3 9 | | 26789 4689 2467 | 23689 23467 1 | (247) (2467) 5 | | 69(27) 69(14) 3 | 69(2) 5 69(47) | 8 (12467) (1247) | +--------------------------------------------------------------------------------------+ | 35(2) 35(4) 8 | 35(1) 9 35(7) | 35(1247) (1247) 6 | | 3569 7 456 | 13568 136 2 | 13459 1489 1348 | | 1 3569 256 | 4 367 35678 | 23579 2789 2378 | +--------------------------------------------------------------------------------------+ | 36(7) 36(1) 9 | 36(12) 8 36(4) | 3(1247) 5 -3(1247) | | 3578 2 157 | 1359 134 3459 | 6 14789 13478 | | 4 13568 156 | 7 1236 3569 | 1239 1289 1238 | +--------------------------------------------------------------------------------------+

That puzzle is tarek's Pearly6000-1812, aka Golden Nugget.

champagne wrote:exactly the situation described by ronk in Fata Morgana with cells r2c4 r5c46 r8c6.

That situation was for tarx0075. Makes me wonder if your other references to Fata Morgana are correct.

[edits: 1) added Golden Nugget alias; 2) added link to earliest known GN post; 3) & 4) color me confused about GN pedigree

]

by **ttt** » Fri Jan 02, 2009 2:51 am

Hmmm…! For Fanta Morgana you can follow here
Don’t talk about FM more…

ttt

by **champagne** » Fri Jan 02, 2009 3:24 am

ronk wrote:That puzzle is tarek's Pearly6000-1812, aka Golden Nugget.

champagne wrote:exactly the situation described by ronk in Fata Morgana with cells r2c4 r5c46 r8c6.

That situation was for tarx0075. Makes me wonder if your other references to Fata Morgana are correct.

[edit: 1) added Golden Nugget alias; 2) added link to earliest known GN post]

You are right edited my post.

Fata Morgana has a very similar start based on three digits

by **ronk** » Fri Jan 02, 2009 10:11 am

champagne wrote:Looking for smaller groups, the solver finds a possibility to eliminate 4r7c2 using 39 sets

Code: Select all
N:......... ......... ......... ......... ......... ....XX... ......... ......... ......... R:.....X... ......... .X.XXX.X. ......X.. XX...X..X ......... .X.XXX.X. ......... ......... C:.X....... ......... X...XXX.. .....X... XX.XXX.X. ......... ..X.X.X.. ......... ......... B:......... ......... ...XX.... ......... ...XX.... ......... ...XX.... ......... ......... 1 2 3 4 5 6 7 8 9

Only two sets for digts '1' and '4'. The corresponding diagram should be relatively easy to analyze

Thanks for the reply, but I can't find anything useful in there.

Are all the Xs above representing base sets (Allan,s sets) or a mix of base sets and cover sets (linksets) :?:

For the N row, is the digit 6 shown at the bottom the row number or the column number? :?:

Also, I find your format much less user friendly than Allan's format of {1R6 3R24568 4R7 5R1269 7R24568}, e.g., for the R row Xs above. Counting over the dots is relatively error prone and not much fun.

by **champagne** » Fri Jan 02, 2009 7:54 pm

ronk wrote:
champagne wrote:Looking for smaller groups, the solver finds a possibility to eliminate 4r7c2 using 39 sets

Code: Select all
N:......... ......... ......... ......... ......... ....XX... ......... ......... ......... R:.....X... ......... .X.XXX.X. ......X.. XX...X..X ......... .X.XXX.X. ......... ......... C:.X....... ......... X...XXX.. .....X... XX.XXX.X. ......... ..X.X.X.. ......... ......... B:......... ......... ...XX.... ......... ...XX.... ......... ...XX.... ......... ......... 1 2 3 4 5 6 7 8 9

Only two sets for digts '1' and '4'. The corresponding diagram should be relatively easy to analyze

Thanks for the reply, but I can't find anything useful in there.

Are all the Xs above representing base sets (Allan,s sets) or a mix of base sets and cover sets (linksets)

For the N row, is the digit 6 shown at the bottom the row number or the column number?

Also, I find your format much less user friendly than Allan's format of {1R6 3R24568 4R7 5R1269 7R24568}, e.g., for the R row Xs above. Counting over the dots is relatively error prone and not much fun.

In my country we say
" the nicest girl can't give more that what she has".

Regarding Allan model, Allan does more than my solver. He has specific tools and a process I could not fully copy up to now.

I can clarify small points:

1) This format is the format agreed with Allan to show a mixed set/linkset group. At that point, there is still some work to do to come to a SLG ; spliit of the "sets" in a Set/Linkset form and normally reshaping slightly the diagram to come to the "nicest form".

2) As such, it proves the elimination (here 4r7c2), so it is normally possible to use it to find alternative way to express the same logic.
I did it for other situations.

3) First line is Row,Column r6c5 r6c6

Let's hope Allan will join us and fulfill your request.

champagne

by **Allan Barker** » Sun Jan 04, 2009 2:33 am

Identical Loops in Tarek-0075 and Golden Nugget Morph
Comparison with Fata Morgana Loop

Following Champagne's logic above, I was looking more closely at Golden Nugget morphs, I was surprised to find a loop identical to the inital loop from tarek-0075. These loops are similar to ones found in other puzzles notably Fata Morgana. The Golden Nugget loop is also 4 layers.

I have placed most the data in the Great Monster Loops thread, including grids and a logic diagrams, including for Fata Morgana. It looks like FM only differs because it is missing the top layer (relative to the diagram) of the other two puzzles.

Golden Nugget Morph Summary

ENMA 47 Nodes, Raw Rank = 4 (linksets - sets)
14 Sets = {1247R2 1247R5 1247R8 46N5}
18 Links = {12c1 47c3 1247c5 14c7 27c9 2n4 8n6 1247b5}
--> (2n4) => r2c4<>3[/code]

.Thumbs Left: Golden Nugget Morph, Right: Tarek-0075.

Code: Select all: Golden Nugget Morph, Initial Loop, notation is NCR +--------------------------------------------------------------------------------------+ | 7 1236 3569 | 1238 1239 1289 | 13568 156 4 | | 36(12) 8 36(4) | -3(1247) 3(1247) 5 | 36(1) 9 36(7) | | 1359 134 3459 | 13478 6 14789 | 2 157 3578 | +--------------------------------------------------------------------------------------+ | 23689 23467 1 | 5 (247) 2467 | 4689 2467 26789 | | 69(2) 5 69(47) | (1247) 8 6(1247) | 69(14) 3 69(27) | | 268 2467 4678 | 9 (1247) 3 | 14568 124567 25678 | +--------------------------------------------------------------------------------------+ | 13568 136 2 | 1348 13459 1489 | 7 456 3569 | | 35(1) 9 35(7) | 6 35(1247) (1247) | 35(4) 8 35(2) | | 4 367 35678 | 2378 23579 2789 | 3569 256 1 | +--------------------------------------------------------------------------------------+

by **champagne** » Sun Jan 04, 2009 3:44 am

Allan Barker wrote:Identical Loops in Tarek-0075 and Golden Nugget Morph
Comparison with Fata Morgana Loop

Looking more closely at Golden Nugget morphs, I was surprised to find a loop identical to the inital loop from tarek-0075. These loops are similar to ones found in other puzzles notably Fata Morgana. The Golden Nugget loop is also 4 layers.

Hi Allan,

Happy to see you again,

I came to the same conclusion as explained some posts above, and I have other examples.

All these puzzle have in common the same property, first seen in Fata Morgana:

some cells (usualy 2, but it can work with more) having a limited number of "free" digits (3 in Fata Morgana, 4 for other examples in your list) 2 of them needed in the solution are such that

If a digit is True in those cells then one at least of two other cells is True as well.

As a matter of fact, these two cells have the same super candidate as the original.

I am working on designing a derived use of your model to find specifically that pattern and include it in the AIC process.

champagne

BTW, you disclose a new loop for the start of Golden Nugget. I used above the loop copied form your website some days ago.

by **Allan Barker** » Sun Jan 04, 2009 4:46 pm

champagne wrote:I came to the same conclusion as explained some posts above, and I have other examples.

Yes, I saw, my post was in support of your's. I added a brief note to mine to clarify.

champagne wrote:BTW, you disclose a new loop for the start of Golden Nugget. I used above the loop copied form your website some days ago.

It is basically the same loop. I used the same old logic, which I called a layer cake, and morphed it to something like tarek-0075. My software then eliminated the need for the set in digit level 6, producing the tarek-0075 look-a-like loop. I think your logical arguments must apply either way.

by **Allan Barker** » Sun Jan 04, 2009 4:54 pm

Hi, Champagne,

Champagne wrote:Looking for smaller groups, the solver finds a possibility to eliminate 4r7c2 using 39 sets
Code: Select all
Diagram for Silver Plate N:......... ......... ......... ......... ......... ....XX... ......... ......... ......... R:.....X... ......... .X.XXX.X. ......X.. XX...X..X ......... .X.XXX.X. ......... ......... C:.X....... ......... X...XXX.. .....X... XX.XXX.X. ......... ..X.X.X.. ......... ......... B:......... ......... ...XX.... ......... ...XX.... ......... ...XX.... ......... ......... 1 2 3 4 5 6 7 8 9

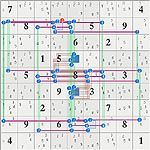
I have found an easy way to work with these (Champagne) diagrams, with the help of a new feature, and this diagram makes a good example. It works this way.

1. Paste the Champagne diagram, I will see the 39 sets, no elimination, yet.
2. I then "Autofill Cover Sets" to find the eliminations. This finds a minimum set of linksets needed to make the eliminations.
3. Optionally, I can then convert (base) sets to linksets to make a standard SLG.

This process assumes that the 39 sets include all base sets required for elimination, in other words, it assumes the only missing sets are weak linksets. For this examples I get:

As Pasted
39 Sets = {1R6 3R24568 4R7 5R1269 7R24568 1C2 3C1567 4C6 5C124568 7C357 6N56 357B4 357B5}
0 Links = {}
Elimination --> none Permutations 1,518,512

Fill with 10 additional linksets
39 Sets = {1R6 3R24568 4R7 5R1269 7R24568 1C2 3C1567 4C6 5C124568 7C357 6N56 357B4 357B5}
10 Links = {7c6 567n2 28n5 28n6 46n8}
Elimination --> r7c2<>4 Permutations 5408

Final Set-Linkset Group, SLG
24 Sets = {3R24568 5R2 7R24568 1C2 4C6 5C124568 6N56 357B4}
25 Links = {1r6 4r7 5r169 3c1567 7c3567 567n2 28n5 28n6 46n8 357b5}
Elimination--> (4r7*7n2) => r7c2<>4 Permutations 3614

Note: this is a rank 1 elimination by the overlap of 4r7 and 7n2.

Also, my solver does not require linksets, the follow will work as well. I checked, the number of permutations is really 9999!

Edit: Changed "my solver does require" to "my solver does not require"

As a Set Group
49 Sets = {1R6 3R24568 4R7 5R1269 7R24568 1C2 3C1567 4C6 5C124568 7C3567 2N56 4N8 5N2 6N2568 7N2 8N56 357B4 357B5}
0 Links = {}
Elimination--> [4R7*7N2] => r7c2<>4 Permutations 9999

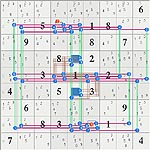
The following diagram shows the location of the 10 extra linksets. In this case the lowercase 'o's show the extra linksets. All are cell sets except for c6n7.

Code: Select all: N:......... ....oo... ......... .......o. .o....... .o..XX.o. .o....... ....oo... ......... R:.....X... ......... .X.XXX.X. ......X.. XX...X..X ......... .X.XXX.X. ......... ......... C:.X....... ......... X...XXX.. .....X... XX.XXX.X. ......... ..X.XoX.. ......... ......... B:......... ......... ...XX.... ......... ...XX.... ......... ...XX.... ......... .........

So, in my country we say "If you want to talk to the nicest girl, maybe you bring your own SLG".

The New Sudoku Players' Forum

Almost Fishes patterns