I've started looking at XY-Chains and have come across something odd!
The image below is from sudoku9981.com (http://www.sudoku9981.com/sudoku-solving/xy-chain.php)
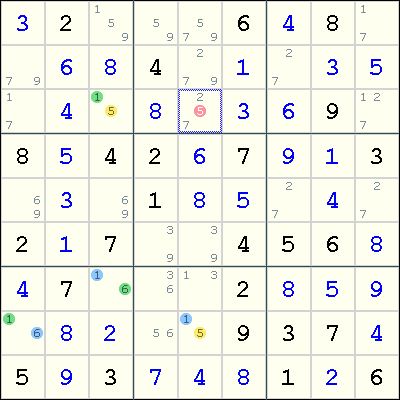
The page explains that there is a xy-chain running from
r3c3 -> r7c3 -> r8c1 -> r8c5.
If you follow the chain in either direction you can prove that r3c5 can't be 5.
Following the chain from r3c3: let r3c3 = 1; r7c3 <> 1 and must be 6; r8c1 <> 6 and must be 1; r8c5 <> 1 and must be 5.
Following the chain from r8c5: let r8c5 = 1; r8c1 <> 1 and must be 6; r7c3 <> 6 and must be 1; r3c3 <> 1 and must be 5.
Both r8c5 and r3c3 can 'see' r3c5, therefore it can not be 5.
So far, so good.
What disturbed me was looking at the "other implications" with following the chain from either direction.
Following the chain from r3c3:
+ If r3c3 = 1 then r1c3 <> 1; if r7c3 = 6 then r5c3 <> 6 and must be 9; if r5c3 = 9 then r1c3 <> 9 and must be 5.
+ if r8c5 = 5 then r8c4 <> 5 and must be 6; if r8c4 = 6 then r7c4 <> 6 and must be 3; if r7c4 = 3 then r6c4 <> 3 and must be 9; if r6c4 = 9 then r1c4 <> 9 and must be 5.
* r1c3 and r1c4 can not both be 5.
So I thought "good I've 'proved' the first direction is false".
Then I followed the chain from r8c5:
+ if r8c1 = 6 then r8c4 <> 6 and must be 5; if r8c4 = 5 then r1c4 <> 5 and must be 9.
+ if r7c3 = 1 then r1c3 <> 1; if r3c3 = 5 then r1c3 <> 5; therefore r1c3 = 9.
* r1c3 and r1c4 can not both be 9.
So, my question is: am I barking mad (or maybe barking up the wrong tree)?
What am I doing wrong!?
cheers
Steve

