The New Sudoku Players' Forum

[kenngyk]

Please help....

[eleven]

Strange, that there was no answer (maybe too short before christmas).

Code: Select all

+------------------+--------------------+-------------------+
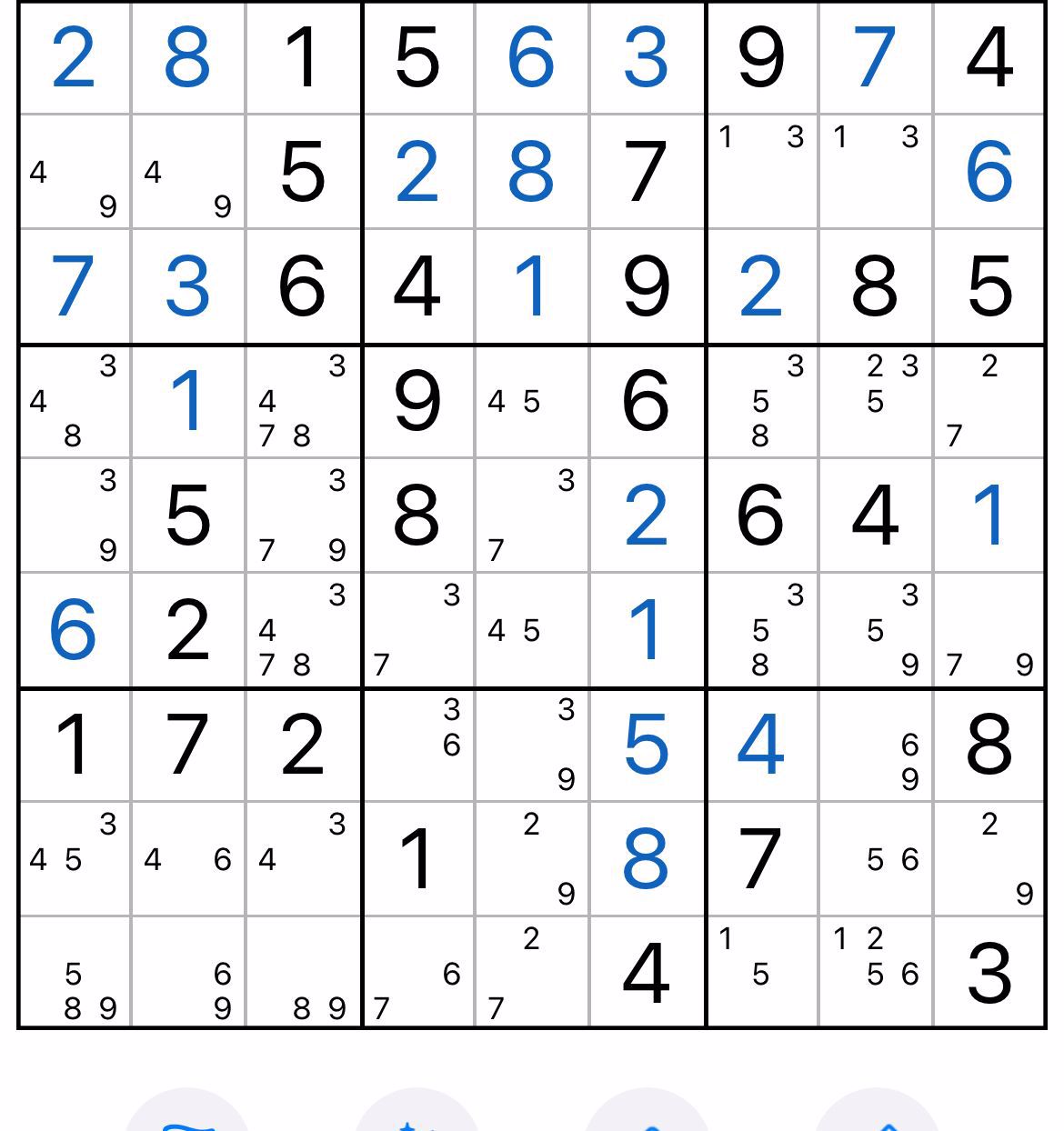
| 2     8     1    |  5     6     3     | 9     7     4     |
| 49    49    5    |  2     8     7     | 13    13    6     |
| 7     3     6    |  4     1     9     | 2     8     5     |
+------------------+--------------------+-------------------+
| 348   1     3478 |  9     45    6     | 358   235   27    |
| 39    5     379  |  8     37    2     | 6     4     1     |
| 6     2     3478 | b37    45    1     | 358   35-9 a79    |
+------------------+--------------------+-------------------+
| 1     7     2    | c36    39    5     | 4    d69    8     |
| 345   46    34   |  1     29    8     | 7     56    2-9   |
| 589   69    89   |  67    27    4     | 15    1256  3     |
+------------------+--------------------+-------------------+

To solve it, you need a short xy-chain (i first found a longer one, which could be shortened to this).
(9=7)r6c9 - (7=3)r6c4 - (3=6)r7c4 - (6=9)r7c8 => -9r8c9,r7c8
In words:
Either r6c9=9 or
r6c9=7,r6c4=3,r7c4=6, and r7c8=9
So 9 must be in r6c9 or r7c8, and you can eliminate 9 in r8c9 and r7c8 (seen by both cells a and d).

[Leren]

Code: Select all

*----------------------------------------*
| 2   8  1    | 5   6  3 | 9   7     4   |
| 49  49 5    | 2   8  7 | 13  13    6   |
| 7   3  6    | 4   1  9 | 2   8     5   |
|-------------+----------+---------------|
| 348 1  3478 | 9   45 6 | 358 235  a27  |
| 39  5  379  | 8   37 2 | 6   4     1   |
| 6   2  3478 |f37  45 1 | 358 359   9-7 |
|-------------+----------+---------------|
| 1   7  2    | 36  39 5 | 4   69    8   |
| 345 46 34   | 1  c29 8 | 7   56   b29  |
| 589 69 89   |e67 d27 4 | 15  1256  3   |
*----------------------------------------*

(7=2) r4c9 - r8c9 = r8c5 - (2=7) r9c5 - r9c4 = (7) r6c4 => - 7 r6c9 stte

In words : if Cell a is not 7 it's 2, so Cell b is not 2, so Cell c is 2, so Cell d is not 2 and is thus 7, so Cell e is not 7 so Cell f is 7.

In summary if Cell a is not 7, Cell f is 7. Since r6c9 sees both Cells a and f it is not 7. The puzzle will solve with singles from there.

Better late than never I guess. Leren