The New Sudoku Players' Forum

[EnderGT]

Partially solved (sorry, I forgot to record the starting positions) - all solutions to date are verified correct by my solver.

Code: Select all

 . . . | . . 1 | 9 . 4
 . . 4 | 3 . . | . 6 .
 . 8 . | 5 . 4 | 7 . 2
 ------+-------+------
 . 7 . | 8 4 . | 3 . 6
 . 4 . | . . 3 | . . .
 . . 6 | . . 9 | . 4 .
 ------+-------+------
 1 6 . | 2 3 7 | 4 5 .
 4 2 . | 9 . 6 | 1 . 3
 . . 3 | 4 1 . | 6 2 .
 

And here's the partial solution with the candidate lists:

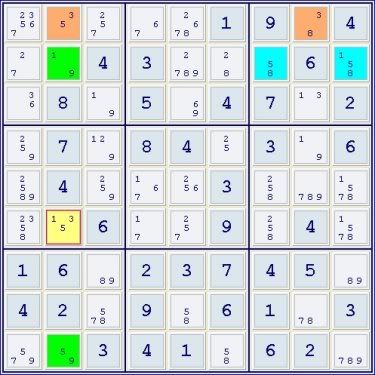
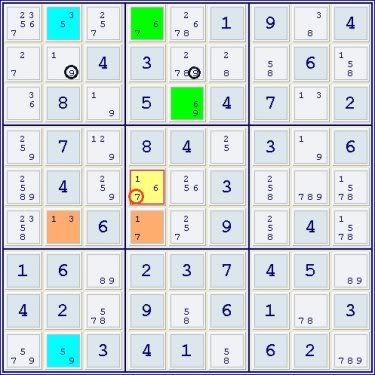
Code: Select all

 *--------------------------------------------------------------------*
 | 23567  35     257    | 67     2678   1      | 9      38     4      |
 | 27     19     4      | 3      2789   28     | 58     6      158    |
 | 36     8      19     | 5      69     4      | 7      13     2      |
 |----------------------+----------------------+----------------------|
 | 259    7      129    | 8      4      25     | 3      19     6      |
 | 2589   4      259    | 167    256    3      | 258    789    1578   |
 | 2358   135    6      | 17     257    9      | 258    4      1578   |
 |----------------------+----------------------+----------------------|
 | 1      6      89     | 2      3      7      | 4      5      89     |
 | 4      2      578    | 9      58     6      | 1      78     3      |
 | 579    59     3      | 4      1      58     | 6      2      789    |
 *--------------------------------------------------------------------*

Simple Sudoku has no more hints. What to do?

[StrmCkr]

a
xy chain
is next..

7 r1c4 -6- r3c5 -9- r3c3 -1- r2c2 -9- r9c2 -5- r9c6 -8- r2c6 -2- r2c1 => r1c13,r2c5<>7


singles from here out...

[EnderGT]

a
xy chain
is next..

7 r1c4 -6- r3c5 -9- r3c3 -1- r2c2 -9- r9c2 -5- r9c6 -8- r2c6 -2- r2c1 => r1c13,r2c5<>7


singles from here out...

Interesting that Simple Sudoku didn't give me a hint for that... maybe I need to stop leaning on the hint


Thanks!

[StrmCkr]

ss isnt programed with
xy chains.

go
look up hodoku

see if your computer can run it for hints.
its really good.

has more advanced steps in it then ss does.

or try us first im sure many of the users here can point out the stuff thats there or alternatives.

we can some what teach whats there as well with examples..

a solver aid can help with that but its also limited to whats in it.

[DonM]

Here's a little 3-set ALS Chain (aka ALS xy-wing rule):



(RC=restricted common)
Green set-> RC=1 -> Blue set -> RC=8 -> Brown set => the 5s in the Green & Brown sets both 'see' the 5 in r6c2, thus r6c2<>5

[EnderGT]

(RC=restricted common)
Green set-> RC=1 -> Blue set -> RC=8 -> Brown set => the 5s in the Green & Brown sets both 'see' the 5 in r6c2, thus r6c2<>5

Woah... you lost me on that one. I don't really understand ALS, that's probably the next technique I should work on learning.

[DonM]

(RC=restricted common)
Green set-> RC=1 -> Blue set -> RC=8 -> Brown set => the 5s in the Green & Brown sets both 'see' the 5 in r6c2, thus r6c2<>5

Woah... you lost me on that one. I don't really understand ALS, that's probably the next technique I should work on learning.

One easy way to see what's going on is to alternately plug in the 1 and 9 in r2c2. The blue color indicates where the restricted common plays a role in linking the sets. For instance, if r2c2=1->naked pair (58) in r2c79->r1c8<>8->r1c8=3->r1c2=5 so r6c2<>5. On the other hand if r2c2=9 then r9c2=5 and there again, r6c2<>5. So either way, r6c2<>5

You can check out the tutorial at: http://forum.enjoysudoku.com/viewtopic.php?t=6443

[DonM]

Here's another 3-Set ALS Chain made possible by the previous one (ie. r6c2<>5):



This example uses a conjugate link:

Green Set-> RC=9 (via conjugate 9s circled in black in r2c25) -> Blue Set -> RC=3 -> Brown Set => r5c4<>7

Don't be confused by the conjugate link. It simply means that the 9 in the Green set 'sees' the 9 in the Blue set just the same as if they were in the same house (row or column or box).

Look at it this way:
If r3c5=9 then r2c5<>9 -> r2c2=9 -> r9c2=5 -> r1c2=3 -> r6c2=1 -> r6c4=7 thus r5c4<>7

And if r3c5=6 then r1c4=7 and r5c4<>7
ie. either way, r3c5=9 or r3c5=6, r5c4<>7.

There's are 2 good reasons that I strongly promote ALS Chains. First and foremost, they are a powerful form of pure pattern-solving if one is not yet very familiar with nice loops or AICs. They are also darn fun if you are using Simple Sudoku as a front-end because of SS's ability to color squares. But second, if you learn how to use them, you become really familiar with ALSs which become very useful later on in nice loops and AICs.

[Allan Barker]

Here is a nice nice loop (continuous) that follows a similar path to DonM's first ALS. It removes r5c2 <> 5 and r1c1 <> 3. This can be viewed in terms of hidden ALS, and DonM's first ALS example also removes 3r1c1. (Solid green and brown lines are stong links)



I agree with DonM's assessment of ALSs, which make one of the more interesting logic families. Although nothing special, the following is a clear illustration of one way ALSs and hidden ALSs can link together. The hidden ALS is in row 9. (Solid blue squares and the solid red lines are stong links/cells)


.

[ronk]

Although nothing special, the following is a clear illustration of one way ALSs and hidden ALSs can link together. The hidden ALS is in row 9. (Solid blue squares and the solid red lines are stong links/cells)


.

This is probably old hat to you, but here goes anyway. (I'm still not comfortable calling an almost-hidden-set (AHS) a hidden-almost-locked-set (hALS) as you do, so I'll stick with AHS for now.)

For your example, the two complementary base sets are:
a) ALS r5c1378 and AHS 167r5 are complementary

b) ALS r8c58 and AHS 57r8 are complementary


By picking one base set from each of the two, four "nominally different" logic sets can be constructed.

Code: Select all

1) ALS r5c1378 and ALS r8c58            2) ALS r5c1378 and AHS 57r8

3) AHS 167r5 and ALS r8c58              4) AHS 167r5 and AHS 57r8

[edit: 1) thanks to Allan, 1567r5 corrected to 167r5; 2) add image; 3) 800px image width was 640px]

[Draco]

Another simple chain that cracks the puzzle:

r9c2=5 r9c6=8 r2c6=2 + r9c2=9 r2c5=9 r2c1=7 ==> r2c15<>2

Singles solve from there.

Cheers...

- drac