- Code: Select all
+-------+-------+-------+
| . . 4 | . 6 . | 7 . . |
| . 8 . | . . . | . 9 . |
| 1 . . | 4 . 7 | . . 6 |
+-------+-------+-------+
| . . 6 | . 8 . | 5 . . |
| 7 . . | 6 . 3 | . . 8 |
| . . 9 | . 2 . | 6 . . |
+-------+-------+-------+
| 3 . . | 9 . 2 | . . 7 |
| . 7 . | . . . | . 8 . |
| . . 1 | . 7 . | 3 . . |
+-------+-------+-------+
..4.6.7...8.....9.1..4.7..6..6.8.5..7..6.3..8..9.2.6..3..9.2..7.7.....8...1.7.3..
Wecoc's puzzle January 19, 2020
4 posts
• Page 1 of 1
Wecoc's puzzle January 19, 2020
- Wecoc
- Posts: 76
- Joined: 08 April 2019
- Location: Girona, Catalonia
Re: Wecoc's puzzle January 19, 2020
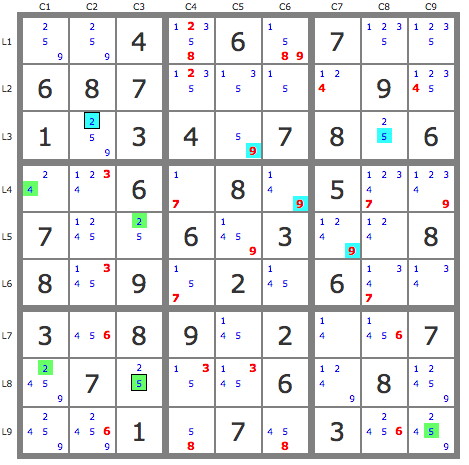
- Code: Select all
+---------------+-----------------+------------------+
| 259 259 4 | 12358 6 1589 | 7 1235 1235 |
| 6 8 7 | 1235 135 15 | 124 9 12345 |
| 1 259 3 | 4 59 7 | 8 25 6 |
+---------------+-----------------+------------------+
| 24 1234 6 | 17 8 149 | 5 12347 12349 |
| 7 1245 25 | 6 1459 3 | 1249 124 8 |
| 8 1345 9 | 157 2 145 | 6 1347 134 |
+---------------+-----------------+------------------+
| 3 456 8 | 9 145 2 | 14 1456 7 |
| 2459 7 25 | 135 1345 6 | 1249 8 12459 |
| 2459 24569 1 | 58 7 458 | 3 2456 2459 |
+---------------+-----------------+------------------+
Easily resolved with TDP
P(2r2c7)=>backdoor
P(2r5c7)=>contradiction=>-2r5c7
P(2r8c7)=>contradiction=>-2r8c7=>stte
Or if you do not want to use contradictions, you can eliminate the common candidates that are eliminated from the development of the three tracks {P (2r2c7, P (2r5c7 and P (2r8c7}) using only the basic technique, which are those shown in the figure. the solution is obtained (stte).
http://www.sitohd.com/siti/23142/portfolio/#i1
The gray cells are the backdoors, those with other colors are candidates which, if assumed to be true, lead to a contradiction using only (Singles and Intersections).
http://www.sitohd.com/siti/23142/foto/414595.jpg
- Ajò Dimonios
- Posts: 213
- Joined: 07 November 2019
Re: Wecoc's puzzle January 19, 2020
Hi,
Another way of using TDP, equivalent to that of Ajo Dimonios, is to construct a network of two conjugated tracks from the 2r3 pair.
- Step 1 development of P(2r3c2) (see puzzle1)
P(2r3c2) : 2r3c2->5r2c8->9r3c5->9r4c6->9r5c7-> ---
P(2r3c2).P'(2r8c3) = P(2r3c2).{-2r8c3-> --- ->2r8c1} => P(2r3c2) does not contain 2r8c7, therefore contains 2r2c7 .
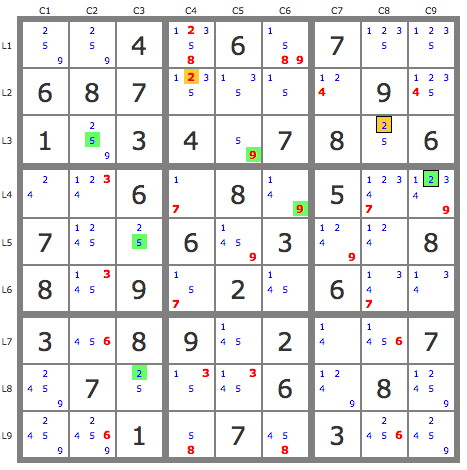
- Step 2 development of P(2r3c8) (see puzzle2)
P(2r3c8) : 2r3c8->2r2c4-> ---
P(2r3c8).P'(2r5c7) = P(2r3c8).{-2r5c7->2r4c9->9r4c6->9r3c5->5r3c2->5r5c3->2r8c3} => P(2r3c2) does not contain 2r8c7, therefore contains 2r5c7 .
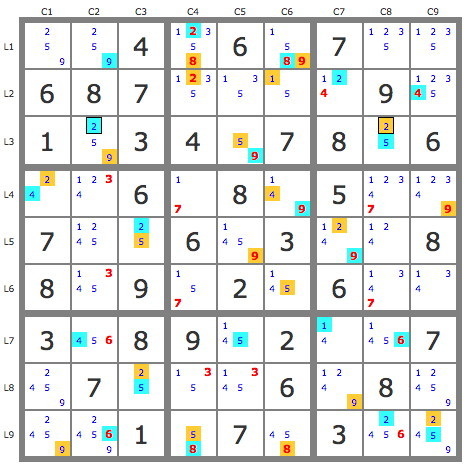
- Step 3 development and intersection of the two tracks (see puzzle3).
From then on, both tracks are easily developed, with only the basic techniques, as on the puzzle3.
This allows the elimination of all candidates who see both colors, and validations r1c1=5, r9c1=9 and r7c7=1.
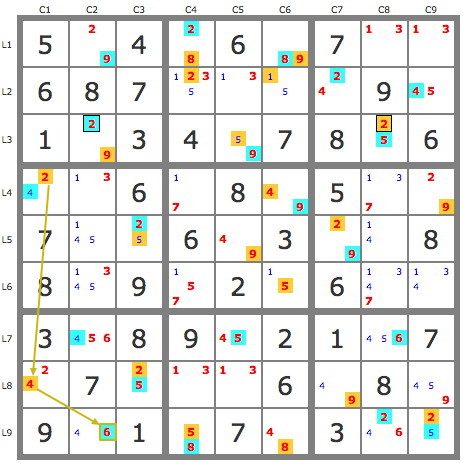
- Step4 end of resolution
After these eliminations, the puzzle is the next one on which the two tracks can be extended to complete the solution, with the 6r9c2 common to both tracks being validated.
Robert
Another way of using TDP, equivalent to that of Ajo Dimonios, is to construct a network of two conjugated tracks from the 2r3 pair.
- Step 1 development of P(2r3c2) (see puzzle1)
P(2r3c2) : 2r3c2->5r2c8->9r3c5->9r4c6->9r5c7-> ---
P(2r3c2).P'(2r8c3) = P(2r3c2).{-2r8c3-> --- ->2r8c1} => P(2r3c2) does not contain 2r8c7, therefore contains 2r2c7 .
puzzle1: Show
- Step 2 development of P(2r3c8) (see puzzle2)
P(2r3c8) : 2r3c8->2r2c4-> ---
P(2r3c8).P'(2r5c7) = P(2r3c8).{-2r5c7->2r4c9->9r4c6->9r3c5->5r3c2->5r5c3->2r8c3} => P(2r3c2) does not contain 2r8c7, therefore contains 2r5c7 .
puzzle2: Show
- Step 3 development and intersection of the two tracks (see puzzle3).
From then on, both tracks are easily developed, with only the basic techniques, as on the puzzle3.
This allows the elimination of all candidates who see both colors, and validations r1c1=5, r9c1=9 and r7c7=1.
puzzle3: Show
- Step4 end of resolution
After these eliminations, the puzzle is the next one on which the two tracks can be extended to complete the solution, with the 6r9c2 common to both tracks being validated.
puzzle4: Show
Robert
- Mauriès Robert
- Posts: 619
- Joined: 07 November 2019
- Location: France
Re: Wecoc's puzzle January 19, 2020
In six steps
1. (1=5)r2c6 - (5=9)r3c5 - r1c6 = (9)r4c6 => -1 r4c6
2. (2)r13c2 = (2-594)r189c1 = (46)r79c2 => -2 r9c2
3. Kraken column (2)r258c7
(2)r2c7 - r3c8 = (2)r3c2
(2-9)r5c7 = r5c5 - r3c5 = (9)r3c2
(2)r8c7 - (2=5)r8c3 - r5c3 = (5)r56c2
=> -5 r3c2
4. (5=8)r9c4 - r1c4 = (8-9)r1c6 = (9-5)r3c5 = (5)r3c8 => -5 r9c8
5. Kraken cell (4569)r9c2
(4)r9c2 - r89c1 = r4c1 - (4=9)r4c6 - r1c6 = (9-5)r3c5 = (5)r3c8
(5)r9c2 - (5=84)r9c46 - r78c5 = (4-9)r5c5 = (9-5)r3c5 = (5)r3c8
(6)r9c2 - r7c2 = (6)r7c8
(9)r9c2 - (9=2)r3c2 - (2=5)r3c8
=> -5 r7c8; five placements
6. (2)r9c8 = r9c1 - r4c1 = r4c89 => -2 r5c8; ste
- Code: Select all
+----------------------+------------------------+-------------------------+
| 259 259 4 | 12358 6 1589 | 7 1235 1235 |
| 6 8 7 | 1235 135 15 | 124 9 12345 |
| 1 29-5 3 | 4 59 7 | 8 25 6 |
+----------------------+------------------------+-------------------------+
| 24 1234 6 | 17 8 49-1 | 5 12347 12349 |
| 7 1245 25 | 6 1459 3 | 1249 124 8 |
| 8 1345 9 | 157 2 145 | 6 1347 134 |
+----------------------+------------------------+-------------------------+
| 3 456 8 | 9 145 2 | 14 146-5 7 |
| 2459 7 25 | 135 1345 6 | 1249 8 12459 |
| 2459 4569-2 1 | 58 7 458 | 3 246-5 2459 |
+----------------------+------------------------+-------------------------+
1. (1=5)r2c6 - (5=9)r3c5 - r1c6 = (9)r4c6 => -1 r4c6
2. (2)r13c2 = (2-594)r189c1 = (46)r79c2 => -2 r9c2
3. Kraken column (2)r258c7
(2)r2c7 - r3c8 = (2)r3c2
(2-9)r5c7 = r5c5 - r3c5 = (9)r3c2
(2)r8c7 - (2=5)r8c3 - r5c3 = (5)r56c2
=> -5 r3c2
4. (5=8)r9c4 - r1c4 = (8-9)r1c6 = (9-5)r3c5 = (5)r3c8 => -5 r9c8
5. Kraken cell (4569)r9c2
(4)r9c2 - r89c1 = r4c1 - (4=9)r4c6 - r1c6 = (9-5)r3c5 = (5)r3c8
(5)r9c2 - (5=84)r9c46 - r78c5 = (4-9)r5c5 = (9-5)r3c5 = (5)r3c8
(6)r9c2 - r7c2 = (6)r7c8
(9)r9c2 - (9=2)r3c2 - (2=5)r3c8
=> -5 r7c8; five placements
- Code: Select all
+---------------------+----------------------+-----------------------+
| 59 59 4 | 1238 6 18 | 7 123 123 |
| 6 8 7 | 1235 135 15 | 124 9 1234 |
| 1 2 3 | 4 9 7 | 8 5 6 |
+---------------------+----------------------+-----------------------+
| 24* 134 6 | 17 8 9 | 5 12347* 1234* |
| 7 145 25 | 6 145 3 | 9 14-2 8 |
| 8 1345 9 | 157 2 145 | 6 1347 134 |
+---------------------+----------------------+-----------------------+
| 3 456 8 | 9 145 2 | 14 146 7 |
| 2459 7 25 | 135 1345 6 | 124 8 59 |
| 2459* 4569 1 | 58 7 458 | 3 246* 59 |
+---------------------+----------------------+-----------------------+
6. (2)r9c8 = r9c1 - r4c1 = r4c89 => -2 r5c8; ste
Cenoman
- Cenoman
- Posts: 3193
- Joined: 21 November 2016
- Location: France
4 posts
• Page 1 of 1