RW wrote:That one has already been classified by Mike Barker as an UR+2kd. See here. Very nice example of the technique in action.
RW
Ah, so it has. I'm not sure how I missed that one all this time. Thanks, RW.
Myth Jellies wrote:ravel wrote:
- Code: Select all
*--------------------------------------------------------------------*
| 56 26 462 | 1458 7 9 | 3 4612 1248 |
| 1 9 4627 | 45+8 3 48 | 45+278 4627 248 |
| 357 37 8 | 45+1 2 6 | 45+7 #147 9 |
|--------------------------------------------------------------------|
| 4 2378 1 | 78 5 2378 | 289 239 6 |
| 368 5 9 | 468 1468 12348 | 248 234 7 |
| 3678 23678 2367 | 46789 4689 23478 | 1 5 2348 |
|----------------------+----------------------+----------------------|
| 2 178 5 | 3 1489 1478 | 6 1479 14 |
| 36789 13678 367 | 2 14689 1478 | 479 13479 5 |
| 3679 4 367 | 679 169 5 | 279 8 123 |
*--------------------------------------------------------------------*
...since its going crazy anyway: what about the elimination rep'nA found in the grid MJ showed above? You have 2 strong links for the 5 and a "finned" strong link for the 4 to eliminate 4 in r2c7.
Hmmm. It is pretty easy to show that when you have just a "strong elbow" in a generic UR(+4, though it doesn't have to be +4)...
- Code: Select all
abX-----abZ
a /|
|
/ a|
|
/ |
abY abW
...the the 'b' candidate in the corner of the elbow is weakly linked to either the 'a' or 'b' candidates in the cell in the opposite corner. In other words, if either 'a' or 'b' are true in the abY-cell then b is false in the abZ-cell, and vice-versa. Any conjugate or strong link between the 'b' in the abY-cell and any grouping of 'b's sharing a house with the abZ-cell will thus kill the 'b' in the abZ-cell. This particular case is in the realm of an AUR, but it is quite obvious to see--probably as easy to spot as a type 3/UR assisted locked set deduction.
*-----------*
|..5|...|83.|
|.3.|7.1|..9|
|...|.6.|...|
|---+---+---|
|...|...|36.|
|1..|.4.|..2|
|.56|...|...|
|---+---+---|
|...|.3.|...|
|2..|6.4|.9.|
|.84|...|7..|
*-----------*
*--------------------------------------------------------------------*
| 67 167 5 | 4 29 29 | 8 3 17 |
| 48 3 28 | 7 5 1 | 6 24 9 |
| 79 24 179 | 38 6 38 | 1245 12457 1457 |
|----------------------+----------------------+----------------------|
| 4789 24 2789 | 1589 1789 5789 | 3 6 14578 |
| 1 79 3789 | 3589 4 6 | 59 578 2 |
| 34789 5 6 | 12389 12789 23789 | 149 1478 1478 |
|----------------------+----------------------+----------------------|
| 5 1679 179 | 128 3 278 | 124 1248 1468 |
| 2 17 137 | 6 178 4 | 15 9 1358 |
| 36 8 4 | 1259 129 259 | 7 12 36 |
*--------------------------------------------------------------------*
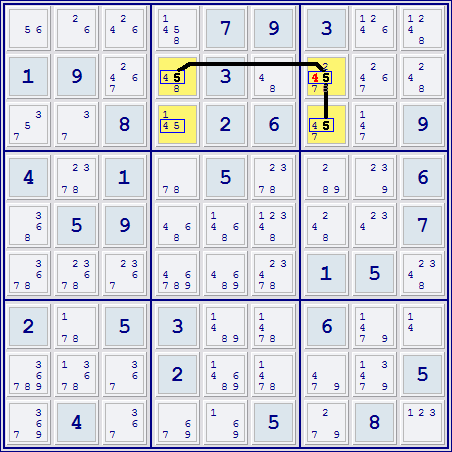
Myth Jellies wrote:ravel wrote:You have 2 strong links for the 5 and a "finned" strong link for the 4 to eliminate 4 in r2c7.
Any conjugate or strong link between the 'b' in the abY-cell and any grouping of 'b's sharing a house with the abZ-cell will thus kill the 'b' in the abZ-cell.
56 26 246 | 1458 7 9 | 3 1246 1248
1 9 2467 | 45+8 3 48 | 45+278 2467 248
357 37 8 | 45+1 2 6 | 45+7 147 9(278)r2c7
||
(8-5)r2c4 = (5)r2c7
||
(7-5)r3c7 = (5)r2c7
||
(1-4)r3c4 = (4)r3c78 ==> r2c7<>4 *--------------------------------------------------------------------*
| 56 26 462 | 1458 7 9 | 3 4612 1248 |
| 1 9 4627 | 45+8 3 48 | 45+278 4627 248 |
| 357 37 8 | 45+1 2 6 | 45+7 147 9 |
|--------------------------------------------------------------------|
| 4 2378 1 | 78 5 2378 | 289 239 6 |
| 368 5 9 | 468 1468 12348 | 248 234 7 |
| 3678 23678 2367 | 46789 4689 23478 | 1 5 2348 |
|----------------------+----------------------+----------------------|
| 2 178 5 | 3 1489 1478 | 6 1479 14 |
| 36789 13678 367 | 2 14689 1478 | 479 13479 5 |
| 3679 4 367 | 679 169 5 | 279 8 123 |
*--------------------------------------------------------------------*
(1) [r2c7]=4 => [r3c78]<>4 => [r3c4]=4
+-----------------------------------+
| . . 4 | 4 . . | . 4 4 |
| . . 4 | 4 . 4 | 4 4 4 |
| . . . | 4 . . | 4 4 . |
|-----------+-----------+-----------|
| 4 . . | . . . | . . . |
| . . . | 4 4 4 | 4 4 . |
| . . . | 4 4 4 | . . 4 |
|-----------+-----------+-----------|
| . . . | . 4 4 | . 4 4 |
| . . . | . 4 4 | 4 4 . |
| . 4 . | . . . | . . . |
+-----------------------------------+
(2) [r2c7]<>5 => [r2c4]=5 and [r3c7]=5
+-----------------------------------+
| 5 . . | 5 . . | . . . |
| . . . | 5 . . | 5 . . |
| 5 . . | 5 . . | 5 . . |
|-----------+-----------+-----------|
| . . . | . 5 . | . . . |
| . 5 . | . . . | . . . |
| . . . | . . . | . 5 . |
|-----------+-----------+-----------|
| . . 5 | . . . | . . . |
| . . . | . . . | . . 5 |
| . . . | . . 5 | . . . |
+-----------------------------------+
| . . . | . . . | . . . |
| . . . | 5 . . | 4 . . |
| . . . | 4 . . | 5 . . |
daj95376 wrote:After staring at this PM for quite awhile, I finally understood. Now, let's hope that I can explain it.
- Code: Select all
+-----------------------------------+
| . . 4 | 4 . . | . 4 4 |
| . . 4 | 4 . 4 | 4 4 4 |
| . . . | 4 . . | 4 4 . |
|-----------+-----------+-----------|
| 4 . . | . . . | . . . |
| . . . | 4 4 4 | 4 4 . |
| . . . | 4 4 4 | . . 4 |
|-----------+-----------+-----------|
| . . . | . 4 4 | . 4 4 |
| . . . | . 4 4 | 4 4 . |
| . 4 . | . . . | . . . |
+-----------------------------------+
- Code: Select all
(2) [r2c7]<>5 => [r2c4]=5 and [r3c7]=5
+-----------------------------------+
| 5 . . | 5 . . | . . . |
| . . . | 5 . . | 5 . . |
| 5 . . | 5 . . | 5 . . |
|-----------+-----------+-----------|
| . . . | . 5 . | . . . |
| . 5 . | . . . | . . . |
| . . . | . . . | . 5 . |
|-----------+-----------+-----------|
| . . 5 | . . . | . . . |
| . . . | . . . | . . 5 |
| . . . | . . 5 | . . . |
+-----------------------------------+
If (1) is true ... then (2) follows ... and [r23c47] would look like ...
- Code: Select all
| . . . | . . . | . . . |
| . . . | 5 . . | 4 . . |
| . . . | 4 . . | 5 . . |
... which is a deadly pattern. Thus, we can conclude that [r2c7]<>4.
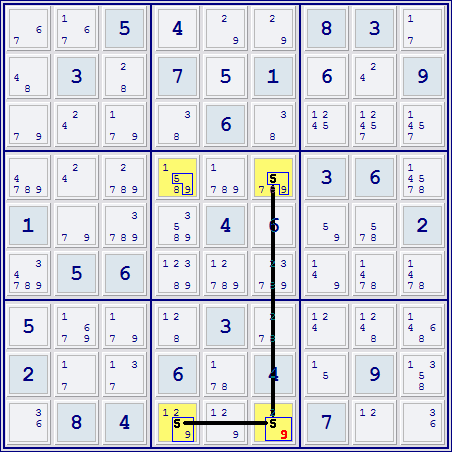
Havard wrote:here is a few more:
Unique Rectangle with 2 strong links:
- Code: Select all
8 4 39 | 13 5 6 | 7 2 19
7 1 2 | 4 9 8 | 6 5 3
69 36 5 | 7 12 23 | 89 48 149
------------------------+-------------------------+------------------------
1349 5 8 | 1369 146 349 | 2 16 7
169 67 79 | 1569U-9 126 259U | 4 3 8
1346 2 34 | 8 7 34 | 59 16 59
------------------------+-------------------------+------------------------
2 78 47 | 56 468 1 | 3 9 45
345 38 6 | 59U 48 459U | 1 7 2
45 9 1 | 2 3 7 | 58 48 6
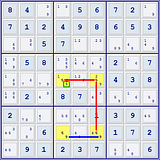
Havard 4-8-06
U meets xwing page 1
With a Unique Rectangle with the numbers [ab] that has two cells with
"extra candidates" ([xabx]), and these cells are on a diagonal from each other
and you have a strong link between any two of the cells in the Rectangle for candidate [a],
then you can eliminate candidate [a] from the cell with extra
candidates that is not part of the strong link.
8 4 39 | 13 5 6 | 7 2 19
7 1 2 | 4 9 8 | 6 5 3
69 36 5 | 7 12 23 | 89 48 149
------------------------+-------------------------+------------------------
1349 5 8 | 1369 146 349 | 2 16 7
169 67 79 | 1569U 126 259U-9 | 4 3 8
1346 2 34 | 8 7 34 | 59 16 59
------------------------+-------------------------+------------------------
2 78 47 | 56 468 1 | 3 9 45
345 38 6 | 59U 48 459U | 1 7 2
45 9 1 | 2 3 7 | 58 48 6 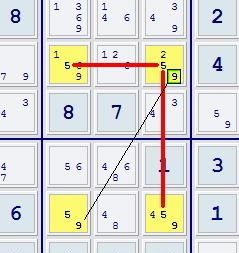
- Code: Select all
*--------------------------------------------------------------------*
| 56 26 462 | 1458 7 9 | 3 4612 1248 |
| 1 9 4627 | 45+8 3 48 | 45+278 4627 248 |
| 357 37 8 | 45+1 2 6 | 45+7 #147 9 |
|--------------------------------------------------------------------|
| 4 2378 1 | 78 5 2378 | 289 239 6 |
| 368 5 9 | 468 1468 12348 | 248 234 7 |
| 3678 23678 2367 | 46789 4689 23478 | 1 5 2348 |
|----------------------+----------------------+----------------------|
| 2 178 5 | 3 1489 1478 | 6 1479 14 |
| 36789 13678 367 | 2 14689 1478 | 479 13479 5 |
| 3679 4 367 | 679 169 5 | 279 8 123 |
*--------------------------------------------------------------------*
...since its going crazy anyway: what about the elimination rep'nA found in the grid MJ showed above? You have 2 strong links for the 5 and a "finned" strong link for the 4 to eliminate 4 in r2c7.
Hmmm. It is pretty easy to show that when you have just a "strong elbow" in a generic UR(+4, though it doesn't have to be +4)...
- Code: Select all
abX-----abZ
a /|
|
/ a|
|
/ |
abY abW
...the 'b' candidate in the corner of the elbow is weakly linked to either the 'a' or 'b' candidates in the cell in the opposite corner. In other words, if either 'a' or 'b' are true in the abY-cell then b is false in the abZ-cell, and vice-versa. Any conjugate or strong link between the 'b' in the abY-cell and any grouping of 'b's sharing a house with the abZ-cell will thus kill the 'b' in the abZ-cell. This particular case is in the realm of an AUR, but it is quite obvious to see--probably as easy to spot as a type 3/UR assisted locked set deduction.
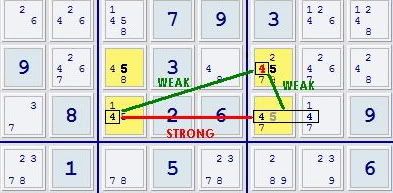
8 4 39 | 13 5 6 | 7 2 19
7 1 2 | 4 9 8 | 6 5 3
69 36 5 | 7 12 23 | 89 48 149
------------------------+-------------------------+------------------------
1349 5 8 | 1369 146 349 | 2 16 7
169 67 79 | 156-9* 126 25-9* | 4 3 8
1346 2 34 | 8 7 34 | 59 16 59
------------------------+-------------------------+------------------------
2 78 47 | 56 468 1 | 3 9 45
345 38 6 | 59* 48 459* | 1 7 2
45 9 1 | 2 3 7 | 58 48 6 *--------------------------------------------------------------------*
| 56 26 462 | 1458 7 9 | 3 4612 1248 |
| 1 9 4627 | 45+8 3 48 | 45+278 4627 248 |
| 357 37 8 | 45+1 2 6 | 45+7 147 9 |
|--------------------------------------------------------------------|
| 4 2378 1 | 78 5 2378 | 289 239 6 |
| 368 5 9 | 468 1468 12348 | 248 234 7 |
| 3678 23678 2367 | 46789 4689 23478 | 1 5 2348 |
|----------------------+----------------------+----------------------|
| 2 178 5 | 3 1489 1478 | 6 1479 14 |
| 36789 13678 367 | 2 14689 1478 | 479 13479 5 |
| 3679 4 367 | 679 169 5 | 279 8 123 |
*--------------------------------------------------------------------* *-----------*
|..8|..5|..2|
|..4|8..|...|
|1..|3..|.8.|
|---+---+---|
|.9.|...|.37|
|...|6.3|...|
|84.|...|.6.|
|---+---+---|
|.3.|..6|..5|
|...|..7|9..|
|2..|4..|7..|
*-----------*
*-----------------------------------------------------------*
| 369 67 8 | 179 4 5 | 136 79 2 |
| 359 2567 4 | 8 267 129 | 356 579 19 |
| 1 2567 569 | 3 2679 29 | 56 8 4 |
|-------------------+-------------------+-------------------|
| 56 9 256 | 125 8 4 | 125 3 7 |
| 57 1 257 | 6 259 3 | 4 59 8 |
| 8 4 3 | 2579 2579 129 | 25 6 19 |
|-------------------+-------------------+-------------------|
| 479 3 179 | 29 129 6 | 8 24 5 |
| 456 8 156 | 25 1235 7 | 9 24 36 |
| 2 56 69 | 4 359 8 | 7 1 36 |
*-----------------------------------------------------------*