The New Sudoku Players' Forum

[sudokumaestro]

Check out these..

http://titacdotpatterns.blogspot.com/

[RW]

Perhaps a tool for someone to help remember what digits are already solved, but I fail to see how this could help you find the next logical step.

Then, some corrections:

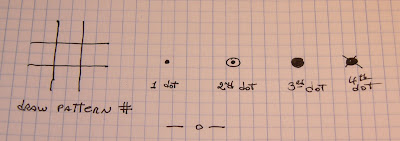
The 4th dot will never be needed.


The second pattern is impossible.


This pattern is impossible.

RW

[sudokumaestro]

You are right RW, I was working late that night and my wires got crossed.
I need to learn how to post pics on this forum, meanwhile I will make the corections.
You make an interesting point and most likely true, because in the advanced puzzles there are not enough digits available for a reasonable deduction.
It has been at the beginning and mid level where I found the TTD's useful. With six numbers solved the patterns fall into a choice of two possibles, generally speaking.
The real reason why I posted them for greater minds to see, is because, I have this hunch that a computer program can be developed using the TTD's .
The TTD's in the basic protocol may prove to be simpler and faster than other programs out there. Wishful thinking?..

Anyways consider this,
if you have, 4 perfect grids in a puzzle
then, there will be a knight and 2 (perpendicularly positioned) axles..
plus, a scale and an airplane
If you overlap the last two, there will be one empty spot.
This is where the (head) triple dot on the knight lies.
more to follow..

[sudokumaestro]

Since I am unable to post pictures here, chek this out

http://titacdotpatterns.blogspot.com/

I have posted a procedure that allows you to solve a part of a puzzle.[/img]

[sudokumaestro]

this is a step by step,
each cell in the TTD grid has a corresponding number,
top row, 1,2,3
mid row, 4,5,6
bottom row,7,8,9

you will notice that the TTD on the number 5 goes like this
double dot on 1, single on 2, single on 6, single on 9
for a total of 5 dots

each grid on the puzzle has a corresponding number
same as the TTD grid
From grids 4 and 7 I dotted the left side POPs
From grids 6 and 9 I dotted the right side POPs

I used the single dots for the 4 and 9 POPs grid
I used the double (plain circle) dot for grids 6 and 7
thereby the sigle dots affect the position of the double dots in two ways,
horizontally from l-grid to r-grid and viceversa
Vertically within each POP grid
( there is no horizontal connection with like dots)

(note, sometimes I put all the POPs in a single grid, it depends on the circumstances. In this case we have the unknowns in grids 4,6,7,9 which happen to form two parallel columns. So I chose the particular format.)

Continuing..
I overlapped both POPs over the TTD on 5
This is the result
cells 1,2,3,4,6, are unchanged
cell 5 is quadrupled
cells 7,8, are doubled
cell 9 is tripled

we can eliminate
the perfect grid, as soon as one double appears
the two empty cells 3 and 4 make it impossible for the bow or the arrow and also the axle
the single on 6 negates a r-scale
the quad and the triple are 5 and 9 (center and corner) eliminating the knight
the singles on 2 and 6 disallow the helicopter

conclusion; the airplane is the only possibility.

second point.
there are two ways in which to construct the airplane

a_ [(9x1)=5, (8x8)=5, (6x9)=5, (5x2)=5]= airplane

b_ [(8x2)=5, (6x1)=5, (5x8)=5, (9x9)=5]= airplane

third point.
We can eliminate the dots on cells (6x2) and (9x8) as possible candidates because they fall into the POPs in the space number 8 (bottom center).
This particular space, if we take into consideration that the airplane possibility is positioned with the top of the pattern to the bottom and to the left.
quote (topside, left bottom)
In this case space number 8 is never used,
therefore no fives will ever be found there.

plus.. when I performed the two options (a and b)
I never mentioned them on the chain.

conclusion, you can assume with a degree of certainty that the number 5 is elsewhere within grids 4 and 9 of the puzzle

then by simple cross counting we deduce that cell (6x2)= 1-8
And cell (9x8)= 9

This is how TTDs and POPs work.

[RW]

Ok... like I guessed in my PM, you are making things unneccessarily complicated.

Here's the current situation on digit 5:

Code: Select all

 *-----------*
 |...|...|5..|
 |...|..5|...|
 |..5|...|...|
 |---+---+---|
 |...|5..|...|
 |X5.|...|.5X|
 |55.|...|.X5|
 |---+---+---|
 |...|.5.|...|
 |X5.|...|.5X|
 |5X.|...|.55|
 *-----------*

Here's the TTD for the solved cells:

Code: Select all

210
001
001

And here's how the candidates are distributed in the unsolved cells:

Code: Select all

000
040
222

-In the completed TTD pattern, all rows and columns must add up to 3.
-Row 2 has only one dot so far, needs two more.
-Only available dots in row 2 are in column 2 => r2c2 must be 2.
-With two dots in r2c2 and the original one dot in r1c2, column two already adds up to 3, r3c2must be 0.
- You may eliminate all candidates 5 that are located in r3c2 of any box => r6c2 and r9c8<>5.

Of course, you could also make the same elimination using the X-wing in r69c19 or the X-wing in r58c28. Which one is easier? It depends. If you are constantly keeping track of your TTD patterns, then this elimination, as described above, should be fairly easy to spot.

If you want to develop your technique further, I'd suggest you look at different examples of X-wing, Swordfish and other fishy eliminations and try to find TTD alternatives to those. But be aware that for every TTD elimination you'll ever find, there's most likely always a fish...

I'd also suggest that you get rid of you handdrawn pictures and come up with a way to post your examples using plain text and BBCode only (see here). Do not expect people to participate in the discussion if it requires scanning and uploading of pictures.

RW

[sudokumaestro]

Code: Select all

*-----------*
|...|.x.|.x.|
|..x|..x|.xx|
|..x|.x.|...|
|---+---+---|
|.7.|...|...|
|...|x.x|...|
|...|...|7..|
|---+---+---|
|7..|...|...|
|...|xx.|.xx|
|...|.x.|.x.|
*-----------*


three 7's solved and the x's are the candidates

A TTD grid with number 7

Code: Select all

110
000
100


The POPs grid looks like this

Code: Select all

020
235
031


In this case I have used the Bow (topside=L-bottom) to eliminate cells (r2c8), (r8c5), (r8c8) as possibles.

Is there another way?

[Glyn]

sudokumaestro Once again in the conventional techniques we would apply an x-wing here. The 7's of rows 1 and 9 are locked in columns 5 and 8. This leads to r3c5,r8c5,r2c8,r8c8 <>7.

[RW]

A TTD grid with number 7

Code: Select all

110
000
100


The POPs grid looks like this

Code: Select all

020
235
031


Without looking at the predefined patterns, I can tell that r2c1 must be 1 (only possibility to reach the sum of 3 in column 1) and r2c3 must be at least 2 (only possibility to reach the sum of 3 in c3), therefore r2c2 must be 0 and we can make the eliminations you described.

However, as Glyn pointed out, there's also an X-wing that makes the same eliminations, plus it also eliminates candidate 7 from r3c5. Don't think you can make the last elimination using your TTD's alone. Or actually, you can if you notice that r3c2 in the TTD must be 1 (r2c1=1 => r2c3=2 => r3c3=1 => r3c2=1) and this one candidate must be in row 9 (all possibilities in row 9 are located in this cell), though in this case I'd say the X-wing is much easier...

RW