The New Sudoku Players' Forum

[Surfertje]

Hi all!



I'm having trouble progressing with a good logic strategy from this position.

On my worksheet I jotted down all the valid permutations of the larger clues (ie, J4, K3 Down, L1 & O1) - with the digits in their correct grid placements. After studying these lists I can struggle my way to a solution by eliminating permutations that don't fit, which sometimes leads to the elimination of a candidate.

Does anyone have a good strategy for breaking through this impasse position? (well, it's an impasse for me, anyway)...or maybe there's something simple that I've overlooked.

Cheers,
Tom

[udosuk]

Tom, thanks for the nice puzzle. And pardon me for the late response.

This one should be able to be solved without T&E, but it'll take me a lot of work to write up an elegant walkthrough.

One "quick and dirty" approach is the use of uniqueness assumption.


If you trust the puzzle creator that it has a unique solution (which it indeed has), it's not hard to see that O7 can't be 5 - since it'll leave MN78 with a deadly pattern: [3498] or [4389].

As a result, O7 is 1 or 6. Now notice O2347, with a sum of 32-9-3=20, can't include the triple {167}. As a result, O3 can't be 6 or 7 and O4 can't be 1.

Also, notice max O34=8+4=12, so min O27=20-12=8. As a result O27 can't be 6+1, implying O2 can't be 6, must be 7. The rest is easy stuff.


On the other hand, if like me you feel unsatisfied with a uniqueness-based solution, there should be a way to crack it "properly". Just give me some time.

[Surfertje]

Thanks so much for your response.

Yours is the first use of uniqueness assumption that I've seen. Very interesting, and it certainly works. However, like you, I feel that it is unsatisfactory.

A couple of days ago I discovered a way to remove the 8 from M3, as follows:-
Only one of K3's permutations with a second-digit 8 (ie, 78164) intersects with an L1 permutation (ie, 87152), while at the same time satisfying M3 = L2.
That leads to a contradiction in O2 and O3 (both=6), and M3 is eliminated.

This permutation analysis was painstaking but satisfying, because it led to a fairly simple solution process after that.

But surely there's a better way.

Cheers...Tom

[udosuk]

But surely there's a better way.

Yes, yes, yes, and I've worked it out!

Step 1:

L2346=23-5=18
M23=24-7=17
=> L2346+M23=18+17=35

LM2=17
LMNOP3=26
=> LM2+LMNOP3=17+26=43

Hence NOP3-L46=43-35=8

But L6 is from {267}
=> L46 can't sum to 2 or 4
=> NOP3 can't sum to 10 or 12, can't be [154|354]
=> O3 can't be 5, must be from {678}


Step 2:

O2347=32-9-3=20 can't contain the triple {678}
=> O7 can't be 6, must be from {15}

Now max NO7=9+5=14
=> min M7=17-14=3
=> M7 can't be 2, must be from {347}

Now min M78=3+4=7
=> max M6=13-7=6
=> M6 can't be 7, must be from {26}


Step 3 (!):

K46=27-8-9=10
L2346=23-5=18
M23=24-7=17
N34=11-7=4
=> K46+L2346+M23+N34=10+18+17+4=49

LM2=17
LMNOP3=26
KLNO4=17-7=10
KLM6=31-4-1-8-3=15
=> LM2+LMNOP3+KLNO4+KLM6=17+26+10+15=68

Hence M6+O34+P3=68-49=19

Now max OP3=8+5=13
=> min M6+O4=19-13=6

But M6 is from {26}, O4 is from {124}
=> Either M6=6 or O4=4, or both
(because they can't be both less than 3)

Hence K46=10 can't be [46], must be [37]!


Step 4:
Now N34=11-7=4=[31]
Also L4 is from {24}, L6 is from {26}
But L2346=23-5=18 can't contain the triple {246}
=> L3 can't be 2|3|4|6, must be from {17}

Also min MNOP3=8+3+6+4=21
=> max L3=26-21=5
=> L3 can't be 7, must be 1
=> MOP3=26-1-3=22=[985] (max values possible)


And the rest is all easy stuff.

Thanks for the great puzzle. Surely a tough ending!

[Surfertje]

Thanks, udosuk, for taking the time to find a solution, and for your very elegant walk-through!!

I had been moderately pleased with my permutation-sweeping strategy that led to the removal M3's 8, but it now seems a bit clunky, even though I still feel that its elegance level is fairly high because it leans on the M3/L2 relationship.

For some time now I've been armed with the knowledge of the row/column difference strategy that Jean-Christophe explains in the "Incredibly difficult kakuro (14x14)" thread, but I had never used it to analyse groups of cells in the way that you have because I hadn't understood it fully.

As the initiator of this thread I've been under pressure to learn that technique because you've used it...and I think that I now understand it!

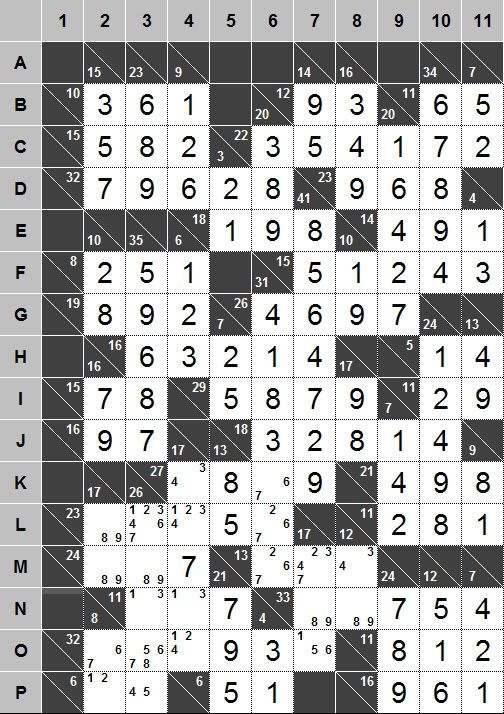
Step 1: I like your strategy to remove the 5 from O3...a nice, intricate, logical assessment!

Step 2: Straightforward.

Step 3: The best and most satisfying move of all because of its increased level of intricacy and that it resulted in the dual-cell solution. The same row/column difference strategy as in Step 1, with a similarly incisive assessment. My only criticism is that you used too few exclamation marks!

Step 4: The elimination of the four digits from L3, leaving {17}, was also pretty neat: I'd never have thought of that. I would have checked my 5-digit numbers list for combinations totalling 23 that comprise 1, 5 and digits from L246. There is only one such combination...91256.

Your terrific walk-through has helped to clear my confusion regarding the non-common cells of the row/column difference strategy, and I've learnt a lot from your method of analysing those cells. Thanks!

Cheers,
Tom

[udosuk]

Tom,

Glad you like my moves. If you want more practicing of row/column difference, be sure to check out this puzzle from Dan (h3lix):

http://www.djape.net/sudoku/wp/index.php/2008/08/02/saturday-special-extra-groups-kakuro/

A brief visual walkthrough is also provided, in case you need some help with the start.

Note I also posted your puzzle here in the forum of that site. Hope you don't mind.

[Surfertje]

Thanks for the link, udosuk. I've downloaded the puzzle but haven't started it yet.

Happy to share 'my' puzzle! I just hope the person who gave it to me doesn't mind, or that I shared it; but then he probably got it from someone else, who got it from......

I'd be interested to see what sort of response your post there will bring!