The New Sudoku Players' Forum

[paulcoz]

Partially completed, Pappocom, Hard puzzle:

Code: Select all

..1|48.|265
68.|...|9..
42.|..6|...
---+---+---
25.|3..|...
8..|.6.|...
...|..8|.92
---+---+---
5..|6..|823
..8|...|..9
9.2|853|4..


I think there may be a unique rectangle in r6c25 & r7c25, yielding a 9 in r7c5, but I'm not sure...somebody said unique rectangles must span no more than two 3x3 squares?

Please explain which techniques and cells I can use to finish this puzzle and provide the next two placements.

Thanks!
Paul.

[Sped]

Code: Select all

 *-----------*
 |..1|48.|265|
 |68.|...|9..|
 |42.|..6|...|
 |---+---+---|
 |25.|3..|...|
 |8..|.6.|...|
 |...|..8|.92|
 |---+---+---|
 |5..|6..|823|
 |..8|...|..9|
 |9.2|853|4..|
 *-----------*


 *-----------------------------------------------------------------------------*
 | 37      379     1       | 4       8       79      | 2       6       5       |
 | 6       8       357     | 1257    1237    1257    | 9       1347    147     |
 | 4       2       3579    | 1579    1379    6       | 137     1378    178     |
 |-------------------------+-------------------------+-------------------------|
 | 2       5       4679    | 3       1479    1479    | 167     1478    14678   |
 | 8       13479   3479    | 12579   6       124579  | 1357    13457   147     |
 | 137     13467   3467    | 157     147     8       | 13567   9       2       |
 |-------------------------+-------------------------+-------------------------|
 | 5       147     47      | 6       1479    1479    | 8       2       3       |
 | 137     13467   8       | 127     1247    1247    | 1567    157     9       |
 | 9       167     2       | 8       5       3       | 4       17      167     |
 *-----------------------------------------------------------------------------*


I don't see any unique rectangles.

X Wing on 3 in r1c12,r8c12 eliminates the 3s in r5c2 and r6c12.
Then line box interaction eliminates the 3s in r23c3.
Line box interaction eliminates the 6 in r6c2.
Multiple colors on 9 sets r1c2=9.
Triple (147) in row 6 and box 4.
A few singles later another 147 triple in box7.

Etc.

[daj95376]

Locked Candidates and a couple Naked Triples is all this puzzle needs.

[Pat]

Code: Select all

 . . 1 | 4 8 . | 2 . 5
 6 . . | . . . | 9 . .
 4 2 . | . . 6 | . . .
-------+-------+------
 2 5 . | 3 . . | . . .
 . . . | . 6 . | . . .
 . . . | . . 8 | . 9 2
-------+-------+------
 . . . | 6 . . | . 2 3
 . . 8 | . . . | . . 9
 9 . 2 | . 5 3 | 4 . .



splendid!
delightfully tricky while not quite "superior"

tarek's definition of a "superior" puzzle:
needs a trio or an X-wing.

[paulcoz]

X Wing on 3 in r1c12,r8c12 eliminates the 3s in r5c2 and r6c12. -> OK
Then line box interaction eliminates the 3s in r23c3. -> OK
Line box interaction eliminates the 6 in r6c2. -> OK
Multiple colors on 9 sets r1c2=9. -> HELP
Triple (147) in row 6 and box 4. -> HELP
A few singles later another 147 triple in box7. -> HELP

Could you explain the last three clues in more detail? Particularly the bit about multiple colours. I don't get it!

Paul.

[re'born]

X Wing on 3 in r1c12,r8c12 eliminates the 3s in r5c2 and r6c12. -> OK
Then line box interaction eliminates the 3s in r23c3. -> OK
Line box interaction eliminates the 6 in r6c2. -> OK
Multiple colors on 9 sets r1c2=9. -> HELP
Triple (147) in row 6 and box 4. -> HELP
A few singles later another 147 triple in box7. -> HELP

Could you explain the last three clues in more detail? Particularly the bit about multiple colours. I don't get it!

Paul.

The Multiple Colors in this case is a skyscraper pattern

Code: Select all

.---------------------.---------------------.---------------------.
| 37     379*   1     | 4      8      79-   | 2      6      5     |
| 6      8      57    | 1257   1237   1257  | 9      1347   147   |
| 4      2      579-  | 1579*  1379   6     | 137    1378   178   |
:---------------------+---------------------+---------------------:
| 2      5      4679  | 3      1479   1479  | 167    1478   14678 |
| 8      1479*  3479  | 12579* 6      124579| 1357   13457  147   |
| 17     147    3467  | 157    147    8     | 13567  9      2     |
:---------------------+---------------------+---------------------:
| 5      147    47    | 6      1479   1479  | 8      2      3     |
| 137    13467  8     | 127    1247   1247  | 1567   157    9     |
| 9      167    2     | 8      5      3     | 4      17     167   |
'---------------------'---------------------'---------------------'


which eliminates 9 from r1c6 and r3c3. From here, locked candidates and singles will take you to:

Code: Select all

 *-----------------------------------------------------------*
 | 3     9     1     | 4     8     7     | 2     6     5     |
 | 6     8     7     | 12    123   5     | 9     134   14    |
 | 4     2     5     | 19    139   6     | 17    137   8     |
 |-------------------+-------------------+-------------------|
 | 2     5     9     | 3     147   14    | 17    8     6     |
 | 8     17*   3     | 1279- 6     129-  | 5     147*  147*  |
 | 17    4     6     | 5     17    8     | 3     9     2     |
 |-------------------+-------------------+-------------------|
 | 5     17    4     | 6     179   19    | 8     2     3     |
 | 17    3     8     | 127   1247  124   | 6     5     9     |
 | 9     6     2     | 8     5     3     | 4     17    17    |
 *-----------------------------------------------------------*


where a naked triple in row 5 will eliminate 1 and 7 from r5c4 and 1 from r5c6. It is then all singles.

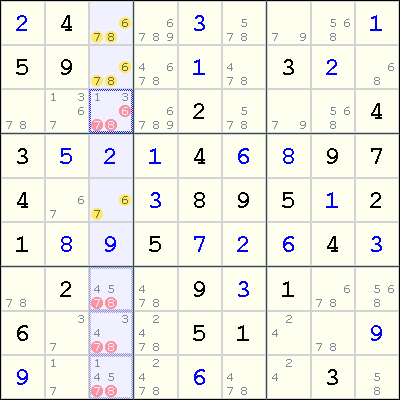
However, daj is correct that you do not need the skyscraper. If you immediately make the locked candidate moves on 3 and 6 (you don't need the x-wing on 3 as all the eliminations come from locked candidates, but it doesn't hurt to do with an x-wing), then the naked triple in row 6 that Sped mentioned arises. Apply this and after some singles and locked candidates, use the naked triple in row 5 that I used above and the puzzle will be unlocked.

[Sped]

X Wing on 3 in r1c12,r8c12 eliminates the 3s in r5c2 and r6c12. -> OK
Then line box interaction eliminates the 3s in r23c3. -> OK
Line box interaction eliminates the 6 in r6c2. -> OK
Multiple colors on 9 sets r1c2=9. -> HELP
Triple (147) in row 6 and box 4. -> HELP
A few singles later another 147 triple in box7. -> HELP

Could you explain the last three clues in more detail? Particularly the bit about multiple colours. I don't get it!

Paul.

After the X Wing and line box interactions, we are here:

Code: Select all

 
 *-----------------------------------------------------------------------------*
 | 37      379a    1       | 4       8       79      | 2       6       5       |
 | 6       8       57      | 1257    1237    1257    | 9       1347    147     |
 | 4       2       579A    | 1579B   1379    6       | 137     1378    178     |
 |-------------------------+-------------------------+-------------------------|
 | 2       5       4679    | 3       1479    1479    | 167     1478    14678   |
 | 8       1479A   3479    | 12579b  6       124579  | 1357    13457   147     |
 | 17      147     3467    | 157     147     8       | 13567   9       2       |
 |-------------------------+-------------------------+-------------------------|
 | 5       147     47      | 6       1479    1479    | 8       2       3       |
 | 137     13467   8       | 127     1247    1247    | 1567    157     9       |
 | 9       167     2       | 8       5       3       | 4       17      167     |
 *-----------------------------------------------------------------------------*


Look at the 9s in column 2. There are exactly two of them, in r5c2 and r1c2. They form a conjugate pair, meaning one must be true for 9 and the other false. Mark them "A" and "a".

Likewise in box 1 there are exactly two 9s, in r1c2 and r3c3. Another conjugate pair. r1c2 is already an "a" so mark r3c3 an "A".

Either all the "A" cells are true for 9 and the "a" cell false, or vice versa.

Now look at the 9s in column 4. There are exactly two of them, in r3c4 and r5c4. Another conjugate pair. Mark them "B" and "b". Either "B" is true for 9 and "b" false, or vice versa.

Since "A" sees both "B" and "b" it cannot be true. "a" must be true.

If "A" is true for 9, then there will either be two 9s in row 3 (if "B" is true) or two 9s in row 5 (if "b" is true). Therefore "A" cannot possibly be true for 9. The "a" must be true for 9.

r1c2=9. Q.E.D.

Then naked singles: 7 in r1c6 and 3 in r1c1, and we're here:

Code: Select all

 
 *--------------------------------------------------------------------*
 | 3      9      1      | 4      8      7      | 2      6      5      |
 | 6      8      57     | 125    123    125    | 9      1347   147    |
 | 4      2      57     | 159    139    6      | 137    1378   178    |
 |----------------------+----------------------+----------------------|
 | 2      5      4679   | 3      1479   149    | 167    1478   14678  |
 | 8      147    3479   | 12579  6      12459  | 1357   13457  147    |
 | 17     147    3467   | 157    147    8      | 13567  9      2      |
 |----------------------+----------------------+----------------------|
 | 5      147    47     | 6      1479   149    | 8      2      3      |
 | 17     13467  8      | 127    1247   124    | 1567   157    9      |
 | 9      167    2      | 8      5      3      | 4      17     167    |
 *--------------------------------------------------------------------*


There's a 147 triple in box 7.

Of course, there's also a 57 pair in column 3, a 147 triple in column 2. There are many ways to solve this.

Daj is correct that you need nothing more than triples and locked candidates, but the steps I listed are the ones I used the first time I solved the puzzle. This was the easiest solving path for me.

YMMV.

[tarek]

As Pat said, the reason why this puzzle was rated as "hard" & not "very hard" (& not a Superior) was the possibilty of solving the puzzle after box line interactions with the hidden double in Row 6 or another one in box 5

tarek

[Plattso]

In words, looking at the Big Board
9 = symbol.

There's two places for symbol in column 2: 1,2 and 5,2.
Suppose it's 5,2.
This eliminates symbol from 5,4 and 5,6, leaving (in box 5) 4,5 and 4,6 as possibles
together with 7,5 and 7,6 makes an x-wing
whose eliminations leave only 3,4 in box 2 for symbol.

This eliminates symbol in 3,3, so box 1 must have symbol in 1,2.

It can't.

Therefore, 5,2 is not 9.

Reminds me of those Bivalue jobbers, where you start and stop with
the same symbol as a chain.

[paulcoz]

Sorry for the delay in replying...

There are a few things listed here I find confusing , but I do understand Sped's explanation (a and A) which leads to the placement of a 9 (conjugate pairs?). From there I am able to solve the puzzle. At last!!

One question: A couple of people have said that there are 147 'triples' in the puzzle (row 6?) and it seems they are talking about the following pattern (from my own list):

147.....147.....47

Can that arrangement in a row, column or 3x3 square be called a triple (despite the fact that one group of candidates is only a pair), or was their candidate list different to mine (147 in all cells)?

Thanks a lot gurus!
Paul.

[udosuk]

You can take a look at the following page:

http://www.sudopedia.org/wiki/Naked_Triple



You should notice that the 3 cells r1c3, r2c3 and r5c3 must together hold all the {6,7,8} in column 3. Therefore other cells in column 3 (r3c3, r7c3, r8c3, r9c3) cannot hold these 3 values {6,7,8}.

The 3 cells do not have to all have the candidates {6,7,8}. Like in this pic, 2 of them have {6,7,8} and one of them {6,7}. As long as there is not a 4th digit in the candidate lists the (naked) triple is formed.

Also, here is a reference to Hidden Pair:

http://www.sudopedia.org/wiki/Hidden_Pair

Which is the most advanced technique you need to solve this puzzle...

[Pat]

A couple of people have said that there are 147 triples in the puzzle
and it seems they are talking about the following pattern:

147 147 47

Can that arrangement in a unit be called a triple
despite the fact that one group of candidates is only a pair?

in a word: yes

3 cells within a unit
all restricted to the possibilities {1,4,7}
= a "naked" trio:
we must reserve those 3 possibilities for those 3 cells