Foreword: I'm going to be posting a bunch here now, I've been pretty active on /r/sudoku but let it suffice to say that a situation has occurred with the moderation. I will be moving my discussions here.
I'm working on documenting a series of techniques with regard to gordonian polygons. A debate has come up over the validity of these techniques and the necessity of proving uniqueness when solving sudoku. Some claim that there exist sudoku with multiple solutions that, when attacked with uniqueness techniques, have only one solution. Thus, uniqueness would have a circular, self-manifesting logic to it. This interests me greatly, but I've yet to see an example of it (or be convinced of its existence!). If someone can provide an example of such a puzzle or proof that no such puzzle exists, I would be greatly appreciative.
The Circular Logic of Uniqueness
33 posts
• Page 1 of 3 • 1, 2, 3
Re: The Circular Logic of Uniqueness
Mizziri wrote:Some claim that there exist sudoku with multiple solutions that, when attacked with uniqueness techniques, have only one solution. Thus, uniqueness would have a circular, self-manifesting logic to it.
yes this can definitely happen
the logic behind uniqueness patterns (unique rectangles, unique loops, BUGs, gurth's ST) is that if the puzzle has a unique solution then a certain pattern cannot exist in the solution, because if it did then you can swap values round and get another solution. the premise of this statement says nothing about what happens if the puzzle you started with has multi solutions. if you have a multi solution puzzle then the "deadly pattern" you are trying to avoid can show up as part of the solution, and if it happens to be the case that the multi solution puzzle has exactly one solution that does not have the deadly pattern then you will find it by applying uniqueness methods.
this is something you have to be wary of occasionally as it means you have to be careful when applying the "self-manifesting logic" to doing sudoku puzzles, for instance, you cannot use uniqueness if you want to do any of the following:
- if you want to prove that a puzzle has a unique solution, rather than assume that it has and then find it; in practice this never really comes up
- or if you're creating a sudoku by hand and want to test its validity
- or if you're doing a variant sudoku (e.g. killer, or samurai) you can't use uniqueness patterns immediately after spotting them unless you validate the extra constraints
the simplest possible example is something like this, with 7 cells remaining:
- Code: Select all
123 12 4|13 5 6|7 8 9
13 6 9|13 7 8|2 4 5
5 7 8|2 4 9|1 3 6
--------+------+-----
12 12 3|8 6 4|9 5 7
8 9 5|7 3 1|6 2 4
7 4 6|5 9 2|3 1 8
--------+------+-----
4 3 1|6 8 7|5 9 2
6 8 2|9 1 5|4 7 3
9 5 7|4 2 3|8 6 1
this puzzle has 3 solutions, but if you try to use uniqueness methods to solve it you'll find only 1 of them depending on which you see first:
- UR 12r14c12 => r1c1 = 3, or
- UR 13r12c14 => r1c1 = 2, or
- BUG+1 => r1c1 = 1
this puzzle seems like a cop out since i just glued two deadly patterns together, so here is a better example: this one showed up in this thread, and it illustrates the last point nicely about not being able to apply uniqueness to variant sudokus - here you cannot apply it to an individual grid in a samurai sudoku because there is no guarantee of it being valid by itself
1to9only wrote:
- Code: Select all
+-------------+-------------+-------------+
| 29 12 79 | 5 3 8 | 17 6 4 |
| 5 8 4 | 17 6 2 | 39 17 39 |
| 6 17 3 | 4 9 17 | 2 8 5 |
+-------------+-------------+-------------+
| 3 27 8 | 27 15 4 | 15 9 6 |
| 1 5 6 | 279 8 79 | 4 237 23 |
| 29 4 79 | 3 15 6 | 157 12 8 |
+-------------+-------------+-------------+
| 8 3 2 | 19 4 19 | 6 5 7 |
| 4 6 1 | 8 7 5 | 39 23 239 |
| 7 9 5 | 6 2 3 | 8 4 1 |
+-------------+-------------+-------------+
this puzzle shown here by itself has multiple solutions, but if you spot the UR 39r28c79 that immediately gives r8c9=2 you'll find that the puzzle reduces to a unique solution fast enough - but in this situation you can't play the UR because this isn't a standalone puzzle and makes the rest of the samurai sudoku invalid
Mizziri wrote:/r/sudoku
oh wow i didn't know reddit had an active sudoku community, last time i checked it was just people posting iphone screenshots of boring all-singles puzzles but that was many years ago. i'm /u/Zapmeister on reddit if you want to message me there
- 999_Springs
- Posts: 591
- Joined: 27 January 2007
- Location: In the toilet, flushing down springs, one by one.
Re: The Circular Logic of Uniqueness
999_Springs wrote:if you have a multi solution puzzle then the "deadly pattern" you are trying to avoid can show up as part of the solution, and if it happens to be the case that the multi solution puzzle has exactly one solution that does not have the deadly pattern then you will find it by applying uniqueness methods.
I see no problem there.
- Proving uniqueness by assuming uniqueness is nonsense.
- Using uniqueness as assumption and investigating both branches - unique/non-unique - no problem even if the goal is to prove the uniqueness.
- Testing whether particular sub-grid can be completed to a valid solution grid - no problem. No need to investigate all branches. If uniqueness assumption leads to contradiction, assume non-uniqueness and repeat.
- dobrichev
- 2016 Supporter
- Posts: 1879
- Joined: 24 May 2010
Re: The Circular Logic of Uniqueness
Thanks for the examples, I wouldn't have thought of sticking multiple deadly patterns together. I'm considering the exercise of proving uniqueness as an extra step in my solving. As for
Do you have an example of this? At least in unique sudokus, all uniqueness techniques are just shortcuts for other techniques. I don't see why that would be different in multi-solution puzzles, but I suppose I've never actually tried to solve a non-unique puzzle. I can't conceive of a puzzle with multiple solutions which doesn't contain some MUG or subset thereof. We how many solutions a puzzle has from its starting point, so any puzzle with a deadly pattern in it is already in a MUG - thus if there were some special uniqueness technique that somehow "broke you out" of the deadly pattern, it could also be applied in unique sudoku. Obviously, no such technique exists for unique puzzles, so unless there's some fundamental difference in how non-unique and unique sudoku can actually be solved (besides uniqueness techniques, obviously), it would seem to me that no such puzzle exists. If it does, it would at least quell the tongue of one infamous nishio fan.
dobrichev's argument of "!uniqueness -> uniqueness, ∴ uniqueness" is pretty strong to me, if for no other reason than pragmatism: If a puzzle with the aforementioned characteristics does exist, we should assume uniqueness because it is useful.
Not particularly high level, but reasonably active and the reddit thread format lends itself nicely to displaying puzzles.
999_Springs wrote:if you have a multi solution puzzle then the "deadly pattern" you are trying to avoid can show up as part of the solution, and if it happens to be the case that the multi solution puzzle has exactly one solution that does not have the deadly pattern then you will find it by applying uniqueness methods.
Do you have an example of this? At least in unique sudokus, all uniqueness techniques are just shortcuts for other techniques. I don't see why that would be different in multi-solution puzzles, but I suppose I've never actually tried to solve a non-unique puzzle. I can't conceive of a puzzle with multiple solutions which doesn't contain some MUG or subset thereof. We how many solutions a puzzle has from its starting point, so any puzzle with a deadly pattern in it is already in a MUG - thus if there were some special uniqueness technique that somehow "broke you out" of the deadly pattern, it could also be applied in unique sudoku. Obviously, no such technique exists for unique puzzles, so unless there's some fundamental difference in how non-unique and unique sudoku can actually be solved (besides uniqueness techniques, obviously), it would seem to me that no such puzzle exists. If it does, it would at least quell the tongue of one infamous nishio fan.
dobrichev's argument of "!uniqueness -> uniqueness, ∴ uniqueness" is pretty strong to me, if for no other reason than pragmatism: If a puzzle with the aforementioned characteristics does exist, we should assume uniqueness because it is useful.
999_Springs wrote:oh wow i didn't know reddit had an active sudoku community, last time i checked it was just people posting iphone screenshots of boring all-singles puzzles but that was many years ago. i'm /u/Zapmeister on reddit if you want to message me there
Not particularly high level, but reasonably active and the reddit thread format lends itself nicely to displaying puzzles.
- Mizziri
- Posts: 3
- Joined: 07 November 2019
Re: The Circular Logic of Uniqueness
Hi Mizziri, and welcome to the forum.
Nice example, 999_Springs. So, if you do use a uniqueness technique in a multi-solution puzzle, I'm presuming all these are possible outcomes depending on the situation:
Btw, here's something about situations where a uniqueness technique apparently can be used correctly without assuming uniqueness. Are there more examples of this? Has anyone seen/used this in a real multi-solution puzzle? (Does anyone actually "solve" multi-solution puzzles?)
Nice example, 999_Springs. So, if you do use a uniqueness technique in a multi-solution puzzle, I'm presuming all these are possible outcomes depending on the situation:
- All but one solution get destroyed, and you can solve the puzzle as if it had a single solution. You'll never know it had many.
- All solutions get destroyed, and you'll run into a contradiction.
- Some but not all solutions get destroyed, and you'll get stuck.
Btw, here's something about situations where a uniqueness technique apparently can be used correctly without assuming uniqueness. Are there more examples of this? Has anyone seen/used this in a real multi-solution puzzle? (Does anyone actually "solve" multi-solution puzzles?)
-

SpAce - Posts: 2671
- Joined: 22 May 2017
Re: The Circular Logic of Uniqueness
Hi Space,
I'm interested in multi-solution puzzles. I'm not sure I understand what you're looking for because of my poor English, but here are two puzzles, the first has two 2 solutions, the second has 3 solutions. I have others in my collection with URs.
..1.7.3...6.5...19.....4.8...2..9.45.........84....1...9.7.....21...5.3...6.2.8..
..342..96.....5..4....6.3..3..9..7...8.....6...9..7..5..5.9....9..1.....12..438..
I agree with what dobrichev says.
Sincerely
Robert
SpAce wrote:Are there more examples of this? Has anyone seen/used this in a real multi-solution puzzle? (Does anyone actually "solve" multi-solution puzzles?)
I'm interested in multi-solution puzzles. I'm not sure I understand what you're looking for because of my poor English, but here are two puzzles, the first has two 2 solutions, the second has 3 solutions. I have others in my collection with URs.
..1.7.3...6.5...19.....4.8...2..9.45.........84....1...9.7.....21...5.3...6.2.8..
..342..96.....5..4....6.3..3..9..7...8.....6...9..7..5..5.9....9..1.....12..438..
I agree with what dobrichev says.
Sincerely
Robert
- Mauriès Robert
- Posts: 619
- Joined: 07 November 2019
- Location: France
Re: The Circular Logic of Uniqueness
Let's look at the original post:
Jimi Hendrix identified the fundamental issue here, IMHO:
If, by "uniqueness techniques", we mean solving methods that exploit the uniqueness of the puzzle solution in order to find candidate eliminations (and I think we do mean this), then "attacking with uniqueness techniques" is an undefined logical process. This is rather like saying "assume 6 = 9", then debating the cosmic significance of the inferred result "2 * 6 = 18". Like, gosh, wow!
There is no circular logic of uniqueness.
Mizziri wrote:Some claim that there exist sudoku with multiple solutions that, when attacked with uniqueness techniques, have only one solution. Thus, uniqueness would have a circular, self-manifesting logic to it.
Jimi Hendrix identified the fundamental issue here, IMHO:
And if 6, turned out to be 9 ...
If, by "uniqueness techniques", we mean solving methods that exploit the uniqueness of the puzzle solution in order to find candidate eliminations (and I think we do mean this), then "attacking with uniqueness techniques" is an undefined logical process. This is rather like saying "assume 6 = 9", then debating the cosmic significance of the inferred result "2 * 6 = 18". Like, gosh, wow!
There is no circular logic of uniqueness.
-

Mathimagics - 2017 Supporter
- Posts: 1926
- Joined: 27 May 2015
- Location: Canberra
Re: The Circular Logic of Uniqueness
(deleted)
Last edited by Leren on Sun Nov 17, 2019 8:10 pm, edited 2 times in total.
- Leren
- Posts: 5212
- Joined: 03 June 2012
Re: The Circular Logic of Uniqueness
I am considering uniqueness techniques, as well as any other technique, as shortcut in brute force branching.
If a particular technique is used in straight forward solving, it also can be used as embedded technique in branching.
Whether the technique is worth using in forward solving is a solver's preference.
Whether the same technique is worth using as embedded technique is also a solver's preference, not necessarily matching the previous preference.
Back to opening post
You have an example, but I still cant understand what "circular, self-manifesting logic" is and how the example provided by 999_Springs proves it.
If a particular technique is used in straight forward solving, it also can be used as embedded technique in branching.
Whether the technique is worth using in forward solving is a solver's preference.
Whether the same technique is worth using as embedded technique is also a solver's preference, not necessarily matching the previous preference.
Back to opening post
Some claim that there exist sudoku with multiple solutions that, when attacked with uniqueness techniques, have only one solution. Thus, uniqueness would have a circular, self-manifesting logic to it. This interests me greatly, but I've yet to see an example of it (or be convinced of its existence!). If someone can provide an example of such a puzzle or proof that no such puzzle exists, I would be greatly appreciative.
You have an example, but I still cant understand what "circular, self-manifesting logic" is and how the example provided by 999_Springs proves it.
- dobrichev
- 2016 Supporter
- Posts: 1879
- Joined: 24 May 2010
Re: The Circular Logic of Uniqueness
(deleted)
Last edited by blue on Sun Nov 17, 2019 4:57 pm, edited 1 time in total.
- blue
- Posts: 1100
- Joined: 11 March 2013
Re: The Circular Logic of Uniqueness
Hi Mizziri,
What do you mean by "unique techniques" ?
If by this term you understand all the resolution techniques that use reasoning that is not based on the assumption that the grid has a single solution (fish, ALS, AICs, coloring, etc...), all these techniques will reduce the puzzle to a situation where the unsolved squares will constitute a configuration that cannot be reduced by these techniques (UR, Bugg, etc...). It is from this situation that we can count the number of solutions.
See for example this puzzle: .2159.6....5.....186..........2......73..85.659.....2..5.63.8.23.9.24........5...
After using the basic techniques, the puzzle is this one, and can no longer be reduced by any technique.
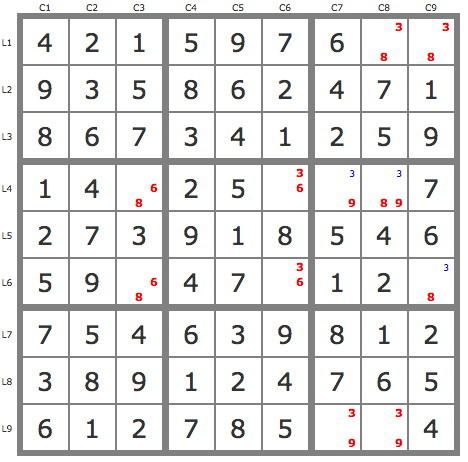
Sincerely
Robert
Mizziri wrote:Foreword: I'm going to be posting a bunch here now, I've been pretty active on /r/sudoku but let it suffice to say that a situationSome claim that there exist sudoku with multiple solutions that, when attacked with uniqueness techniques, have only one solution. Thus, uniqueness would have a circular, self-manifesting logic to it. This interests me greatly, but I've yet to see an example of it (or be convinced of its existence!). If someone can provide an example of such a puzzle or proof that no such puzzle exists, I would be greatly appreciative.
What do you mean by "unique techniques" ?
If by this term you understand all the resolution techniques that use reasoning that is not based on the assumption that the grid has a single solution (fish, ALS, AICs, coloring, etc...), all these techniques will reduce the puzzle to a situation where the unsolved squares will constitute a configuration that cannot be reduced by these techniques (UR, Bugg, etc...). It is from this situation that we can count the number of solutions.
See for example this puzzle: .2159.6....5.....186..........2......73..85.659.....2..5.63.8.23.9.24........5...
After using the basic techniques, the puzzle is this one, and can no longer be reduced by any technique.

Sincerely
Robert
- Mauriès Robert
- Posts: 619
- Joined: 07 November 2019
- Location: France
Re: The Circular Logic of Uniqueness
Hi Robert,
How did you get that far? Your puzzle state has three solutions:
...but the original puzzle has seven, and as far as I understand, should have got stuck already here:
Did you take a guess at some point?
--
Added.
In what way and why? I don't know what the point is in trying to solve them because you have to take at least one guess to proceed. I have no interest in that. That's why I'm also quite happy to use uniqueness techniques because I only solve valid puzzles voluntarily. Uniqueness patterns are often easy to spot (complicated MUGs etc aside) and using them is fun and effective. I see no reason to cripple my solving abilities with an artificial restriction that might force me to use something much less elegant.
I don't consider it my job to prove the uniqueness of the solution because it's something I already know when I start solving a puzzle -- at least if I use Hodoku as usual. If I solve an unknown puzzle on paper, then I don't know it, but if I get stuck and the reason turns out to be multiple solutions, then I know I will never touch another puzzle from that source. It's the puzzle provider's responsibility to guarantee the validity of the puzzle, or to at least inform if it has multiple solutions.
That said, I fully realize it's not the only way to see things. It's just my opinion. Nevertheless, I'm interested in what exactly you do with multi-solution puzzles as they can't be logically solved to the end. I'd also like to see your last part of the TDP introduction. I think you said it deals with uniqueness issues?
I was looking for examples of the idea RW demonstrated in the linked thread. It would allow to use uniqueness techniques safely even without any guarantees that the puzzle is valid, apparently by checking that the uniqueness pattern can't actually have multiple solutions if it can be influenced from the outside. It doesn't of mean that the technique could solve real multi-solution puzzles any further than other techniques.
Mauriès Robert wrote:See for example this puzzle: .2159.6....5.....186..........2......73..85.659.....2..5.63.8.23.9.24........5...
After using the basic techniques, the puzzle is this one, and can no longer be reduced by any technique.
How did you get that far? Your puzzle state has three solutions:
- Code: Select all
.----------.----------.-------------.
| 4 2 1 | 5 9 7 | 6 38 38 |
| 9 3 5 | 8 6 2 | 4 7 1 |
| 8 6 7 | 3 4 1 | 2 5 9 |
:----------+----------+-------------:
| 1 4 68 | 2 5 36 | 39 389 7 |
| 2 7 3 | 9 1 8 | 5 4 6 |
| 5 9 68 | 4 7 36 | 1 2 38 |
:----------+----------+-------------:
| 7 5 4 | 6 3 9 | 8 1 2 |
| 3 8 9 | 1 2 4 | 7 6 5 |
| 6 1 2 | 7 8 5 | 39 39 4 |
'----------'----------'-------------'
...but the original puzzle has seven, and as far as I understand, should have got stuck already here:
- Code: Select all
.------------.---------------.----------------.
| 47 2 1 | 5 9 37 | 6 38 348 |
| 9 3 5 | 48 68 26 | 24 7 1 |
| 8 6 47 | 137 147 12 | 239 5 39 |
:------------+---------------+----------------:
| 14 14 68 | 2 5 367 | 39 389 78 |
| 2 7 3 | 9 14 8 | 5 14 6 |
| 5 9 68 | 34 67 136 | 14 2 378 |
:------------+---------------+----------------:
| 17 5 47 | 6 3 9 | 8 14 2 |
| 3 8 9 | 17 2 4 | 17 6 5 |
| 6 14 2 | 78 178 5 | 1379 39 349 |
'------------'---------------'----------------'
Did you take a guess at some point?
--
Added.
Mauriès Robert wrote:SpAce wrote:Are there more examples of this? Has anyone seen/used this in a real multi-solution puzzle? (Does anyone actually "solve" multi-solution puzzles?)
I'm interested in multi-solution puzzles.
In what way and why? I don't know what the point is in trying to solve them because you have to take at least one guess to proceed. I have no interest in that. That's why I'm also quite happy to use uniqueness techniques because I only solve valid puzzles voluntarily. Uniqueness patterns are often easy to spot (complicated MUGs etc aside) and using them is fun and effective. I see no reason to cripple my solving abilities with an artificial restriction that might force me to use something much less elegant.
I don't consider it my job to prove the uniqueness of the solution because it's something I already know when I start solving a puzzle -- at least if I use Hodoku as usual. If I solve an unknown puzzle on paper, then I don't know it, but if I get stuck and the reason turns out to be multiple solutions, then I know I will never touch another puzzle from that source. It's the puzzle provider's responsibility to guarantee the validity of the puzzle, or to at least inform if it has multiple solutions.
That said, I fully realize it's not the only way to see things. It's just my opinion. Nevertheless, I'm interested in what exactly you do with multi-solution puzzles as they can't be logically solved to the end. I'd also like to see your last part of the TDP introduction. I think you said it deals with uniqueness issues?
I'm not sure I understand what you're looking for
I was looking for examples of the idea RW demonstrated in the linked thread. It would allow to use uniqueness techniques safely even without any guarantees that the puzzle is valid, apparently by checking that the uniqueness pattern can't actually have multiple solutions if it can be influenced from the outside. It doesn't of mean that the technique could solve real multi-solution puzzles any further than other techniques.
Last edited by SpAce on Mon Nov 18, 2019 1:25 am, edited 1 time in total.
-

SpAce - Posts: 2671
- Joined: 22 May 2017
Re: The Circular Logic of Uniqueness
SpAce, I have a few problems with your assumption, though I like your technique of enumerating all possible outcomes.
In Case 1, there can exist a deadly pattern in the end result. Consider how avoidable rectangles work, but note that we can also have a complex deadly pattern in the solution which a human would be VERY bad at detecting. Since this discussion is more about the epistemology of solving rather than practical techniques, I'm going to assume that we are solving under arbitarily large amounts of time and have perfect logical reasoning and extremely good pattern recognition. That is to say that we COULD spot a deadly pattern in the solution, even if it might be monstrously difficult.
Case 2 is not possible by definition. If there were some elimination, !X, caused by a uniqueness technique that resulted in no solutions for the puzzle, this technique would be simply be restated as a logical technique: If !X -> no solution, therefore X. This cannot happen, since we have defined our premise to be that there are no logical techniques which advance us in the puzzle.
The last part of your post delves into the idea of sub-puzzles and is very interesting. I can't speak much to it though, but it appears to be completely logical. I have never touched a multi-solution puzzle, and I only know of one person who acknowledges their existence in normal solving, which is to say that he is intent on proving the uniqueness of his solution in every puzzle that he solves.
Mathimagics, let me clarify my position to you: I don't believe uniqueness is a circular argument, and I think we should assume uniqueness and ALWAYS use it when possible. That said, I think the uniqueness assumption has not been examined thoroughly.
dobrichev, I like (and agree with) your premise that every candidate elimination is a shortcut for brute forcing. 999_Springs' example is not precisely what I was looking for, and I was admittedly not very clear in what I requested. I'll clarify now. I would like to see a puzzle with multiple solutions such that there is exactly one uniqueness technique (defined below) which causes the puzzle to have a solution. If such a puzzle existed (and I will note that I believe it does not), then there would be an example of uniqueness proving itself. Let me know if this explanation is sufficient.
I meant to say 'uniqueness technique,' which I will define thus:
The elimination of a candidate whose verity would cause the puzzle to have multiple solutions.
I believe this definition is precise and comprehensive.
As for your example, I believe you used uniqueness (or guessed) in some way earlier in your solution. Sudoku wiki solver is unable to reach this state in the puzzle, as is Hodoku. It apparently has seven solutions, not the three displayed in your end state.
In Case 1, there can exist a deadly pattern in the end result. Consider how avoidable rectangles work, but note that we can also have a complex deadly pattern in the solution which a human would be VERY bad at detecting. Since this discussion is more about the epistemology of solving rather than practical techniques, I'm going to assume that we are solving under arbitarily large amounts of time and have perfect logical reasoning and extremely good pattern recognition. That is to say that we COULD spot a deadly pattern in the solution, even if it might be monstrously difficult.
Case 2 is not possible by definition. If there were some elimination, !X, caused by a uniqueness technique that resulted in no solutions for the puzzle, this technique would be simply be restated as a logical technique: If !X -> no solution, therefore X. This cannot happen, since we have defined our premise to be that there are no logical techniques which advance us in the puzzle.
The last part of your post delves into the idea of sub-puzzles and is very interesting. I can't speak much to it though, but it appears to be completely logical. I have never touched a multi-solution puzzle, and I only know of one person who acknowledges their existence in normal solving, which is to say that he is intent on proving the uniqueness of his solution in every puzzle that he solves.
Mathimagics, let me clarify my position to you: I don't believe uniqueness is a circular argument, and I think we should assume uniqueness and ALWAYS use it when possible. That said, I think the uniqueness assumption has not been examined thoroughly.
dobrichev, I like (and agree with) your premise that every candidate elimination is a shortcut for brute forcing. 999_Springs' example is not precisely what I was looking for, and I was admittedly not very clear in what I requested. I'll clarify now. I would like to see a puzzle with multiple solutions such that there is exactly one uniqueness technique (defined below) which causes the puzzle to have a solution. If such a puzzle existed (and I will note that I believe it does not), then there would be an example of uniqueness proving itself. Let me know if this explanation is sufficient.
Mauriès Robert wrote:Hi Mizziri,
What do you mean by "unique techniques" ?
I meant to say 'uniqueness technique,' which I will define thus:
The elimination of a candidate whose verity would cause the puzzle to have multiple solutions.
I believe this definition is precise and comprehensive.
As for your example, I believe you used uniqueness (or guessed) in some way earlier in your solution. Sudoku wiki solver is unable to reach this state in the puzzle, as is Hodoku. It apparently has seven solutions, not the three displayed in your end state.
- Mizziri
- Posts: 3
- Joined: 07 November 2019
Re: The Circular Logic of Uniqueness
Hi Mizziri,
I guess your point is that the remark "You'll never know it had many" is not accurate? I must agree, at least in theory. I said it based on the assumption that the player doesn't know beforehand that there's a possibility that the puzzle has multiple solutions, so it never occurs to them to double-check the solution grid (and even if they do, the DP might be very difficult to spot, as you said).
Is this a verified result, and without any qualifications? That would be interesting because it would mean that using uniqueness techniques even in a multi-solution puzzle is always safe, i.e. it would never destroy all solutions. Is that true? It's exactly what I'd like to know. Your reasoning sounds logical, but I can't really think it through with my non-existent experience with multi-solution puzzles.
Where was that premise defined, and does it affect the previous result? Does it make any practical sense anyway? If we know that there are no logical techniques available (which we can't without an omniscient software solver), then we know that the puzzle must have multiple solutions and we shouldn't use uniqueness techniques, right? I certainly use them as soon as I spot such opportunities instead of even trying to exhaust all other possibilities.
Yes, it sounds interesting. That's why I'd love to see practical examples of it, if anyone has them.
Some people are masochists like that -- even some participating in this discussion Robert, for example, and if I remember correctly, 999_Springs as well. Nothing wrong with that if one wants to do things the hard way. Personally I don't see any practical reason for it, though.
Robert, for example, and if I remember correctly, 999_Springs as well. Nothing wrong with that if one wants to do things the hard way. Personally I don't see any practical reason for it, though.
I'm not sure if that's entirely accurate. First, I think you should talk about causing multiple sub-puzzle solutions, as a valid puzzle as a whole can never have more than one (a multi-solution sub-puzzle would cause a contradiction in the full puzzle). Secondly, as Leren once taught me, there's something unintuitive about certain uniqueness patterns even in the sub-puzzle level. Some BUGs, BUG-Lites, and I would presume MUGs too (not sure of that), are actually no-solution deadly patterns! I don't think many people are aware of that. It certainly surprised me, but it's true.
I got the same result.
Mizziri wrote:SpAce wrote:So, if you do use a uniqueness technique in a multi-solution puzzle, I'm presuming all these are possible outcomes depending on the situation:Is that a correct assumption? In the last case, is it possible to rinse and repeat with the same three possible outcomes?
- All but one solution get destroyed, and you can solve the puzzle as if it had a single solution. You'll never know it had many.
- All solutions get destroyed, and you'll run into a contradiction.
- Some but not all solutions get destroyed, and you'll get stuck.
SpAce, I have a few problems with your assumption, though I like your technique of enumerating all possible outcomes.
In Case 1, there can exist a deadly pattern in the end result. ... That is to say that we COULD spot a deadly pattern in the solution, even if it might be monstrously difficult.
I guess your point is that the remark "You'll never know it had many" is not accurate? I must agree, at least in theory. I said it based on the assumption that the player doesn't know beforehand that there's a possibility that the puzzle has multiple solutions, so it never occurs to them to double-check the solution grid (and even if they do, the DP might be very difficult to spot, as you said).
Case 2 is not possible by definition. If there were some elimination, !X, caused by a uniqueness technique that resulted in no solutions for the puzzle, this technique would be simply be restated as a logical technique: If !X -> no solution, therefore X.
Is this a verified result, and without any qualifications? That would be interesting because it would mean that using uniqueness techniques even in a multi-solution puzzle is always safe, i.e. it would never destroy all solutions. Is that true? It's exactly what I'd like to know. Your reasoning sounds logical, but I can't really think it through with my non-existent experience with multi-solution puzzles.
This cannot happen, since we have defined our premise to be that there are no logical techniques which advance us in the puzzle.
Where was that premise defined, and does it affect the previous result? Does it make any practical sense anyway? If we know that there are no logical techniques available (which we can't without an omniscient software solver), then we know that the puzzle must have multiple solutions and we shouldn't use uniqueness techniques, right? I certainly use them as soon as I spot such opportunities instead of even trying to exhaust all other possibilities.
SpAce wrote:Btw, here's something about situations where a uniqueness technique apparently can be used correctly without assuming uniqueness.
The last part of your post delves into the idea of sub-puzzles and is very interesting. I can't speak much to it though, but it appears to be completely logical.
Yes, it sounds interesting. That's why I'd love to see practical examples of it, if anyone has them.
I have never touched a multi-solution puzzle, and I only know of one person who acknowledges their existence in normal solving, which is to say that he is intent on proving the uniqueness of his solution in every puzzle that he solves.
Some people are masochists like that -- even some participating in this discussion
I meant to say 'uniqueness technique,' which I will define thus:
The elimination of a candidate whose verity would cause the puzzle to have multiple solutions.
I believe this definition is precise and comprehensive.
I'm not sure if that's entirely accurate. First, I think you should talk about causing multiple sub-puzzle solutions, as a valid puzzle as a whole can never have more than one (a multi-solution sub-puzzle would cause a contradiction in the full puzzle). Secondly, as Leren once taught me, there's something unintuitive about certain uniqueness patterns even in the sub-puzzle level. Some BUGs, BUG-Lites, and I would presume MUGs too (not sure of that), are actually no-solution deadly patterns! I don't think many people are aware of that. It certainly surprised me, but it's true.
As for your example, I believe you used uniqueness (or guessed) in some way earlier in your solution. Sudoku wiki solver is unable to reach this state in the puzzle, as is Hodoku. It apparently has seven solutions, not the three displayed in your end state.
I got the same result.
-

SpAce - Posts: 2671
- Joined: 22 May 2017
Re: The Circular Logic of Uniqueness
Hi Mizziri,
When examining multiple solutions puzzle you should know that an empty solution grid is such a puzzle too.
Surely this isn't your question.
Note also, that a puzzle can contain a deadly pattern(s) but still be incompletable to any valid solution grid due to contradiction(s) outside of the deadly pattern.
If you define set of acceptable solving techniques, with some using uniqueness, then the result of your solving process will entirely depend on the details which technique what proves and it is up to you to define these rules.
To my knowledge no widely known solving program exists that uses uniqueness by not assuming that the given puzzle has unique solution. Even if such program exists, its behaviour will be specific to its particular implementation.
Believe me, brute force (or nesting chains of unlimited depth if you prefer) is dealing pretty well with multiple solution and with invalid puzzles, and does exactly what you told it to do. I don't want to discuss whether a formal approach which does its work is logical or illogical or whatever. Accepting or rejecting it is up to you.
Some exotic multiple solution puzzles have been discussed in this forum and I can give you links but I doubt they are what you are looking for.
So, you are asking for an example where after applying unspecified techniques, tailored to each other in a unspecified way and each relying on unspecified assumptions, the result will be X or Y, independently of these uncertainties.
Explain the problem for yourself and you will find the answer.
For a technique described as "if certain conditions are met then you CAN eliminate these and these candidates" the devil is in the details how to interpret the result and what to do next.
Mizziri wrote:I would like to see a puzzle with multiple solutions such that there is exactly one uniqueness technique (defined below) which causes the puzzle to have a solution. If such a puzzle existed (and I will note that I believe it does not), then there would be an example of uniqueness proving itself. Let me know if this explanation is sufficient.
When examining multiple solutions puzzle you should know that an empty solution grid is such a puzzle too.
Surely this isn't your question.
Note also, that a puzzle can contain a deadly pattern(s) but still be incompletable to any valid solution grid due to contradiction(s) outside of the deadly pattern.
If you define set of acceptable solving techniques, with some using uniqueness, then the result of your solving process will entirely depend on the details which technique what proves and it is up to you to define these rules.
To my knowledge no widely known solving program exists that uses uniqueness by not assuming that the given puzzle has unique solution. Even if such program exists, its behaviour will be specific to its particular implementation.
Believe me, brute force (or nesting chains of unlimited depth if you prefer) is dealing pretty well with multiple solution and with invalid puzzles, and does exactly what you told it to do. I don't want to discuss whether a formal approach which does its work is logical or illogical or whatever. Accepting or rejecting it is up to you.
Some exotic multiple solution puzzles have been discussed in this forum and I can give you links but I doubt they are what you are looking for.
So, you are asking for an example where after applying unspecified techniques, tailored to each other in a unspecified way and each relying on unspecified assumptions, the result will be X or Y, independently of these uncertainties.
Explain the problem for yourself and you will find the answer.
For a technique described as "if certain conditions are met then you CAN eliminate these and these candidates" the devil is in the details how to interpret the result and what to do next.
- dobrichev
- 2016 Supporter
- Posts: 1879
- Joined: 24 May 2010
33 posts
• Page 1 of 3 • 1, 2, 3

