http://forum.enjoysudoku.com/viewtopic.php?t=6411
In that thread, I stated to the effect that even if turned out that eliminations using the almost Sue De Coq (SDC) pattern could be replicated by other means, since I am always looking for the complete SDC anyway, the finding of an almost SDC will still be useful because it both provides a relatively obvious menu of weak links and yet, it is no more assumptive than a simple ALS and just as easy to apply.
After further experience looking for and applying the almost SDC, it is becoming clearer to me that this is more than just an occasionally useful pattern in advanced solving. First, it turns out that the almost SDC is actually relatively common in puzzles. Typically, during a puzzle almost SDC patterns often present themselves and then are almost just as often destroyed as the solving process continues, but likewise, as candidates are removed in certain cells, new almost SDC patterns present themselves. (However, few almost SDCs go on to be full SDCs.) Second, by the very nature of the SDC pattern, it turns out that sometimes more than the ‘usual’ weak link exit points are immediately available in a way that you wouldn’t ordinarily find with other patterns. Third, as the example below indicates, more than one elimination is sometimes possible with one almost SDC pattern.
Finally, is the fact that it no longer matters to me (if it ever did) whether the eliminations possible from a full SDC or an almost SDC can be replicated by other means, mainly because while it may be easy enough to backtrack from a presented SDC or almost SDC based elimination and produce a comparable elimination by other means, it is not necessarily as easy to do so if presented with the puzzle and the SDC or almost SDC not identified. For instance, a SDC can often be replicated by a doubly-linked ALS pattern, but even though I have reasonable experience finding basic doubly-linked ALSs (the examples of those patterns in The ALS Chains Tutorial are mine), while I can find a SDC fairly quickly, I can’t nearly as easily find the associated doubly-linked ALS. Furthermore, I would probably miss it altogether unless I had already found the associated SDC.
Overall, the usefulness of the almost SDC depends upon two main factors: One is the use of the simplified directions for finding a basic SDC:
In a row or column within the same box, look for a core of 4 digit values in 2 cells or 5 digit values in 3 cells. Now, on that same row or column, look for a bivalue cell where the digits are the same as 2 of those in the core. Then, in the same box as the core, look for a bivalue cell with 2 digits from the core, but not the same digits as in the other bivalue cell. If the above are present, then on that row or column, you can eliminate all the digits equal to the digits in the bivalue cell on the same row or column and in the box that contains the core, you can eliminate all the digits equal to the bivalue cell there. You can also eliminate all digits in the row or column or in the box equal to any digit still remaining in the core but not present in the two bivalue cells.
(Please see
http://forum.enjoysudoku.com/viewtopic.php?t=6410&postdays=0&postorder=asc&start=0 for descriptions of the more advanced SDC patterns.)
The other factor is that the almost SDC pattern presents an immediate menu of weak link exits without any further search necessary. Since, considering the power of the pattern, IMO, one should be looking for SDC anyway, the finding of almost SDC patterns is just a straightforward natural progression.
The following examples from a single puzzle illustrate points made above:
Original Puzzle:
- Code: Select all
. 3 .|1 . 9|. 6 .
. . 1|. . .|9 2 .
6 . .|. . .|. 4 1
-----+-----+-----
. . .|7 3 .|. . .
7 . .|. 2 .|. . 8
. . .|. 9 6|. . .
-----+-----+-----
8 5 .|. . .|. . 4
. 6 2|. . .|5 . .
. 4 .|2 . 7|. 8 .
Puzzle as presented in examples (this is very close to the SSTS position):
- Code: Select all
.---------------------.---------------------.---------------------.
| 2 3 458 | 1 478 9 | 78 6 57 |
| 45 78 1 | 34568 4678 458 | 9 2 357 |
| 6 789 589 | 358 78 2 | 38 4 1 |
:---------------------+---------------------+---------------------:
| 459 1289 45689 | 7 3 1458 | 146 159 269 |
| 7 19 34569 | 45 2 145 | 1346 1359 8 |
| 345 128 3458 | 458 9 6 | 1347 1357 237 |
:---------------------+---------------------+---------------------:
| 8 5 7 | 69 16 3 | 2 19 4 |
| 139 6 2 | 489 148 48 | 5 1379 379 |
| 139 4 39 | 2 5 7 | 136 8 369 |
'---------------------'---------------------'---------------------'

But for the 2 in r6c9, the basic Sue De Coq pattern is present: the core blue cells (an aals with 1,3,5,7,9 in 3 cells, r456c8), the brown cell A, r6c9, with 3,7 and the green cell C, r7c8, with 1,9. The logic is straightforward: If not 2 in r6c9 then the Sue De Coq is true and any of the circled green cells are valid weak link ‘targets’. However, some additional targets are immediately available (though indirectly): Since the 3s in r56c7 and the 7 in r6c7 are all targets, due to the aals pattern in r456c7, 1 and 6 can be used individually or as a block in r9c7: aals(37=146)r456c7 - (16)r9c7. Of course, they are available indirectly and that has to be indicated in any notation, but the point is that these targets are almost as obvious and as available for use as the regular targets are and due to the very construct of a SDC and the possible eliminations, these extra ‘obvious’ targets likely occur frequently enough to make it worthwhile to be on the watch for them. They may also help simplify chains as shown later on below.
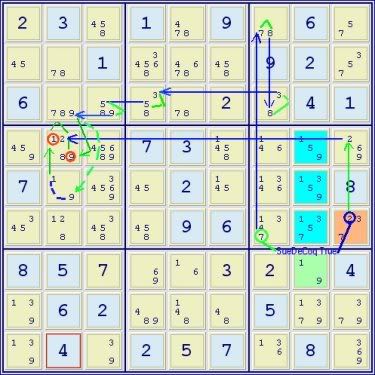
This is the same grid at the same point as the previous example. The blue lines indicate strong links, the green lines, weak links. The path to the eliminations should be relatively easy to figure out. The 9 in r4c2 is eliminated first and then the chain is continued from r3c2 to r5c2 as indicated by the interrupted lines leading to the elimination of the 1 in r4c2. Needless to say, the removal of 2 candidates in one cell leaving available strong links in r4c2 and for the 1 and 9 in c2 is a very helpful way to start the solution of this puzzle.
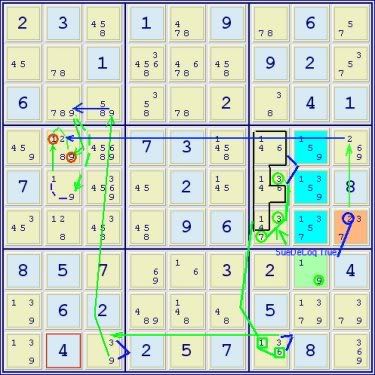
This is the same set of eliminations as in the previous example, but instead using the additional ‘indirect’ targets as described in the first example. The simpler chain path as compared to the previous one should be obvious. Just to be clear, it is not inferred that the aals pattern in r456c7 is some sort of previously unrecognized pattern. On the contrary, the pattern itself would be obvious to experienced solvers. What is of interest is the fact that it is so easy to pick out as a possible part of an almost SDC pattern and that since it may occur as part of some almost SDC patterns, it adds to the potentially available ‘menu’ of weak link targets.

Finally, is a third elimination at the same point in the puzzle used in the previous examples, but using a totally different pathway. The chain should be self-explanatory. Note that this elimination must come after the first two eliminations since it destroys the almost SDC pattern.
Therefore, in these examples a single almost SDC produces 3 potentially useful eliminations near the beginning of a difficult puzzle. All of them were picked out fairly quickly once the almost SDC was identified. The real point here is not that there are no other ways to achieve these eliminations, but that once one is familiar with the SDC pattern itself, this may well be the easiest way to find these particular eliminations. (FWIW: one particular alternative chain to achieve the above elimination does not require the almost SDC, but does require the previous two eliminations.)
(Puzzle credit: This is the UK forum Weekly Extreme #112. Of possible interest: it has already been discussed on this forum close to this point of the puzzle (almost the SSTS position) with some early solving already shown ( http://forum.enjoysudoku.com/viewtopic.php?t=6453&start=0 ))

