The New Sudoku Players' Forum

[mith]

Code: Select all

+-------+-------+-------+
| 9 . . | . . . | . . . |
| . . 8 | 7 . . | . . 6 |
| . 5 . | . 4 . | . 3 . |
+-------+-------+-------+
| . 2 . | . 3 . | . 5 . |
| . . 6 | 8 . . | . . 7 |
| . . . | . . . | 6 . . |
+-------+-------+-------+
| . . . | . . 4 | . . . |
| . . 7 | 1 . . | . . 8 |
| . 1 . | . 2 . | . 4 5 |
+-------+-------+-------+
9..........87....6.5..4..3..2..3..5...68....7......6.......4.....71....8.1..2..45

[pjb]

After 2 MSLSs and 2 jellyfish, the following results:

Code: Select all

 9       67      234    | 235    68     1      | 25     78     24     
 1234   e34      8      | 7      59     2359   | 245    19     6     
 67      5       12     | 29     4      68     | 78     3      19     
------------------------+----------------------+---------------------
 78      2       149    | 469    3      67     | 189    5      149   
 1345    49-3    6      | 8      159    259    | 234    129    7     
a135     78      345    | 245    1579   259    | 6      1289   234   
------------------------+----------------------+---------------------
b235     68      2359   | 359    78     4      | 19     67     1239   
 2345   d349     7      | 1      569    359    | 23     269    8     
 68      1      c39     | 369    2      78     | 79     4      5     


then
(3)r6c1 = (3)r7c1 - (3=4)r8c2,r9c3 - (4=3)r2c2 => -3 r5c2; stte

Phil

[denis_berthier]

That's a mith puzzle as I like them, with lots of (Naked, Hidden and Super-Hiden) Subsets.
This one requires bivalue-chains in addition to Subsets.

Hidden Text: Show

***********************************************************************************************
*** SudoRules 20.1.s based on CSP-Rules 2.1.s, config = BC+S
*** Using CLIPS 6.32-r773
***********************************************************************************************
234 candidates, 1590 csp-links and 1590 links. Density = 5.83%
hidden-pairs-in-a-block: b8{r7c5 r9c6}{n7 n8} ==> r9c6 ≠ 9, r9c6 ≠ 6, r9c6 ≠ 3, r7c5 ≠ 9, r7c5 ≠ 6, r7c5 ≠ 5
hidden-pairs-in-a-block: b1{r1c2 r3c1}{n6 n7} ==> r3c1 ≠ 2, r3c1 ≠ 1, r1c2 ≠ 4, r1c2 ≠ 3
biv-chain[2]: b1n6{r1c2 r3c1} - r9n6{c1 c4} ==> r1c4 ≠ 6
biv-chain[2]: b1n6{r3c1 r1c2} - c5n6{r1 r8} ==> r8c1 ≠ 6
swordfish-in-columns: n6{c2 c5 c8}{r7 r1 r8} ==> r8c6 ≠ 6, r7c4 ≠ 6, r7c1 ≠ 6, r1c6 ≠ 6
swordfish-in-columns: n8{c2 c5 c8}{r6 r7 r1} ==> r7c1 ≠ 8, r6c1 ≠ 8, r1c7 ≠ 8, r1c6 ≠ 8
swordfish-in-rows: n7{r3 r4 r9}{c7 c1 c6} ==> r7c7 ≠ 7, r6c6 ≠ 7, r6c1 ≠ 7, r1c7 ≠ 7
hidden-pairs-in-a-block: b3{r1c8 r3c7}{n7 n8} ==> r3c7 ≠ 9, r3c7 ≠ 2, r3c7 ≠ 1, r1c8 ≠ 2, r1c8 ≠ 1
hidden-pairs-in-a-block: b4{r4c1 r6c2}{n7 n8} ==> r6c2 ≠ 9, r6c2 ≠ 4, r6c2 ≠ 3, r4c1 ≠ 4, r4c1 ≠ 1
hidden-triplets-in-a-row: r1{n6 n7 n8}{c5 c2 c8} ==> r1c5 ≠ 5, r1c5 ≠ 1
hidden-triplets-in-a-column: c1{n6 n7 n8}{r9 r3 r4} ==> r9c1 ≠ 3
hidden-triplets-in-a-column: c6{n6 n7 n8}{r3 r4 r9} ==> r4c6 ≠ 9, r4c6 ≠ 1, r3c6 ≠ 9, r3c6 ≠ 2, r3c6 ≠ 1
naked-pairs-in-a-block: b2{r1c5 r3c6}{n6 n8} ==> r3c4 ≠ 6
hidden-triplets-in-a-row: r7{n6 n7 n8}{c2 c8 c5} ==> r7c8 ≠ 9, r7c8 ≠ 2, r7c8 ≠ 1, r7c2 ≠ 9, r7c2 ≠ 3
naked-pairs-in-a-block: b7{r7c2 r9c1}{n6 n8} ==> r8c2 ≠ 6
swordfish-in-columns: n1{c1 c5 c8}{r2 r5 r6} ==> r6c9 ≠ 1, r6c6 ≠ 1, r6c3 ≠ 1, r5c7 ≠ 1, r5c6 ≠ 1, r2c7 ≠ 1, r2c6 ≠ 1
hidden-single-in-a-column ==> r1c6 = 1
swordfish-in-rows: n4{r2 r5 r8}{c2 c7 c1} ==> r6c1 ≠ 4, r4c7 ≠ 4, r1c7 ≠ 4
biv-chain[3]: r8n4{c1 c2} - r2c2{n4 n3} - c6n3{r2 r8} ==> r8c1 ≠ 3
biv-chain[3]: b6n3{r6c9 r5c7} - c7n4{r5 r2} - r1c9{n4 n2} ==> r6c9 ≠ 2
jellyfish-in-columns: n9{c2 c8 c5 c6}{r8 r5 r6 r2} ==> r8c7 ≠ 9, r6c9 ≠ 9, r6c4 ≠ 9, r6c3 ≠ 9, r5c7 ≠ 9, r2c7 ≠ 9
hidden-pairs-in-a-block: b3{r2c8 r3c9}{n1 n9} ==> r3c9 ≠ 2, r2c8 ≠ 2
naked-quads-in-a-column: c7{r1 r2 r5 r8}{n2 n5 n4 n3} ==> r9c7 ≠ 3, r7c7 ≠ 3, r7c7 ≠ 2
x-wing-in-rows: n3{r1 r9}{c3 c4} ==> r7c4 ≠ 3, r7c3 ≠ 3, r6c3 ≠ 3
x-wing-in-rows: n3{r6 r7}{c1 c9} ==> r5c1 ≠ 3, r2c1 ≠ 3
biv-chain[3]: c7n3{r8 r5} - c7n4{r5 r2} - r2c2{n4 n3} ==> r8c2 ≠ 3
biv-chain[3]: r2c2{n3 n4} - r8c2{n4 n9} - r9c3{n9 n3} ==> r1c3 ≠ 3
stte

[Mauriès Robert]

Hi mith,
This puzzle has interesting loops on 6, 7 and 8.
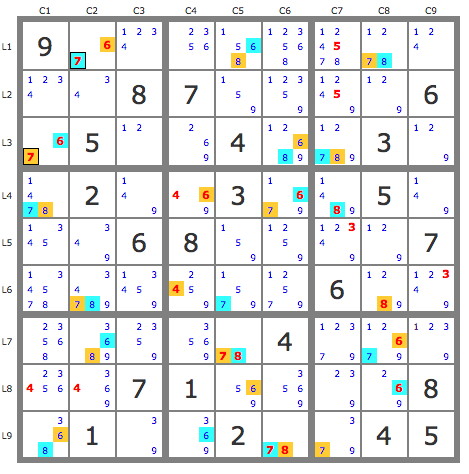
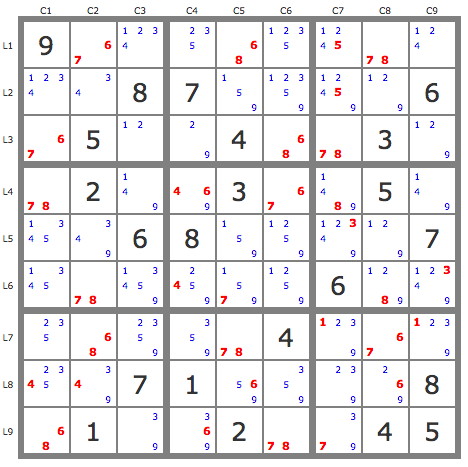
This makes it possible to construct two conjugated tracks P(7r1c2) and P(7r3c1) marked respectively in blue and yellow on the puzzle1, giving 37 eliminations of candidates who simultaneously see a candidate from each track. The puzzle is then reduced to puzzle 2.

puzzle1: Show

puzzle2: Show

The elimination is continued with :
- jellyfish on the 9
- swordfish on the 1
- basic techniques
- two X-wings on the 3
and finally by the anti-track P'(3r6c1) : (-3r6c1)=>3r7c1->9r9c3->9r5c2 => -3r5c2 => r6c1=3.
The basic techniques complete the puzzle.
Robert