The New Sudoku Players' Forum

[ixsetf]

Hidden Text: Show

Code: Select all

+-------+-------+-------+
| 4 9 . | 1 . . | . 2 . |
| 1 5 . | . 2 . | . . 3 |
| . . 6 | . . 3 | 1 . . |
+-------+-------+-------+
| 9 . . | 5 . 1 | . . 7 |
| . 8 . | . 6 . | 9 . . |
| . . 7 | 9 . 4 | . 8 . |
+-------+-------+-------+
| . . 9 | . 1 . | 6 . . |
| 8 . . | . . 2 | . 4 . |
| . 7 . | 3 . . | . . 5 |
+-------+-------+-------+


Play this puzzle online at the Daily Sudoku site.

The minimized version of this is probably too hard to do by hand, but I'll post it in case anyone wants to try it out.

Hidden Text: Show

Code: Select all

+-------+-------+-------+
| 4 . . | 1 . . | . 2 . |
| . 5 . | . . . | . . 3 |
| . . 6 | . . 3 | 1 . . |
+-------+-------+-------+
| . . . | 5 . . | . . 7 |
| . 8 . | . 6 . | 9 . . |
| . . 7 | . . 4 | . 8 . |
+-------+-------+-------+
| . . 9 | . 1 . | 6 . . |
| 8 . . | . . 2 | . 4 . |
| . 7 . | 3 . . | . . . |
+-------+-------+-------+


Play this puzzle online at the Daily Sudoku site.

[Leren]

I'll start things off by solving the easier version in 1 move :

Code: Select all

*------------------------------------------------------------------------*
| 4      9      3       | 1     b57     568     |ha57-8A  2      68      |
| 1      5      8       | 467    2      69      |  47     679    3       |
| 7      2      6       | 48     459C   3       |  1      59B    489     |
|-----------------------+-----------------------+------------------------|
| 9      346    24      | 5      8      1       |  234    36     7       |
| 35     8      145     | 2      6      7       |  9      135    14      |
| 256    16     7       | 9      3      4       |  25     8      126     |
|-----------------------+-----------------------+------------------------|
|e235    34     9       | 478    1     d58      |  6      37    f28      |
| 8      136    15      | 67    c579    2       |  37     4      19      |
| 26     7      124     | 3      49     689     | g28     19     5       |
*------------------------------------------------------------------------*

8 r1c7 - 7 r1c7 = r1c5 - 5 r1c5  =  r8c5 - r7c6 = (5-2) r7c1 = r7c9 - (2=8) r9c7 - 8 r1c7 => - 8 r1c7; lclste
                                 |
8 r1c7 - 5 r1c7 = r3c8 - 5 r3c5 /

Leren

[ArkieTech]

Code: Select all

 *--------------------------------------------------*
 | 4    9    3    | 1    57  a568  | 578  2   b68   |
 | 1    5    8    | 467  2    69   | 47   679  3    |
 | 7    2    6    | 48   459  3    | 1    59   489  |
 |----------------+----------------+----------------|
 | 9    346  24   | 5    8    1    | 234  36   7    |
 | 35   8    145  | 2    6    7    | 9    135  14   |
 | 256  16   7    | 9    3    4    | 25   8    126  |
 |----------------+----------------+----------------|
 | 235  34   9    | 478  1   a58   | 6    37  b28   |
 | 8    136  15   | 67   579  2    | 37   4    19   |
 | 26   7    124  | 3    49   69-8 |c28   19   5    |
 *------------------------------------------- lclste*
(8=6)r17c6=(6=2)r17c9-(2=8)r9c7 => -8r9c6;

[Leren]

I'm going out on a limb here and suggesting that the harder form of the puzzle can be converted to the easier form by noting that with respect to the diagonal from Top Left to Bottom Right (TLBR) there is a pairing of clues in the mirror cells as follows: 1 <> 9, 2 <> 8, 3 <> 7, 4 <> 4, 5 <> 5, 6 <> 6, 7 <> 3, 8 <> 2, 9 <> 1

This is the PM for the harder version following basics:

Code: Select all

*--------------------------------------------------------------------------------*
| 4       39      38       | 1       5789    56789    | 578     2       5689     |
| 1279    5       128      | 246789  24789   6789     | 478     679     3        |
| 279     29      6        | 24789   245789  3        | 1       579     4589     |
|--------------------------+--------------------------+--------------------------|
| 12369   123469  1234     | 5       2389    189      | 234     136     7        |
| 1235    8       12345    | 27      6       17       | 9       135     1245     |
| 123569  12369   7        | 29      239     4        | 235     8       1256     |
|--------------------------+--------------------------+--------------------------|
| 235     234     9        | 478     1       578      | 6       37      258      |
| 8       136     135      | 679     579     2        | 37      4       159      |
| 1256    7       1245     | 3       4589    5689     | 258     159     12589    |
*--------------------------------------------------------------------------------*

Now look for mirror cells wrt the TLBR diagonal where the number of candidates is not the same.

For example, r1c2 = 39 and it's mirror cell is r2c1. Because of the clue paring r2c1 can only be 7 (the clue pair of 3) or 1 (the clue pair of 9) , so 2 and 9 can be removed there.

Similarly r3c1 <> 9, r4c1 = 9 (the clue pair of the given cell r1c4 = 1) etc etc.

Proceeding in this way for the whole PM and applying basics I suspect that we will arrive at the post basics PM for the easier version of the puzzle, or possibly something even simpler.

So am I a Dunce, a DUX, or something in between ?

Leren

PS I've also noticed from the solution that wrt the other diagonal the following pairings also apply : 1 <> 1, 2 <> 3, 3 <> 2, 4 <> 5, 5 <> 4, 6 <> 6, 7 <> 8, 8 <> 7, 9 <> 9. Is it possible to deduce this from the clue distribution ?

Leren

[ixsetf]

I'm going out on a limb here and suggesting that the harder form of the puzzle can be converted to the easier form by noting that with respect to the diagonal from Top Left to Bottom Right (TLBR) there is a pairing of clues in the mirror cells as follows: 1<> 9, 2<> 8, 3<> 7, 4 <> 4, 5<> 5, 6<> 6, 7<> 3, 8<> 2, 9<> 1

This is the PM for the harder version following basics:

Code: Select all

*--------------------------------------------------------------------------------*
| 4       39      38       | 1       5789    56789    | 578     2       5689     |
| 1279    5       128      | 246789  24789   6789     | 478     679     3        |
| 279     29      6        | 24789   245789  3        | 1       579     4589     |
|--------------------------+--------------------------+--------------------------|
| 12369   123469  1234     | 5       2389    189      | 234     136     7        |
| 1235    8       12345    | 27      6       17       | 9       135     1245     |
| 123569  12369   7        | 29      239     4        | 235     8       1256     |
|--------------------------+--------------------------+--------------------------|
| 235     234     9        | 478     1       578      | 6       37      258      |
| 8       136     135      | 679     579     2        | 37      4       159      |
| 1256    7       1245     | 3       4589    5689     | 258     159     12589    |
*--------------------------------------------------------------------------------*

Now look for mirror cells wrt the TLBR diagonal where the number of candidates is not the same.

For example, r1c2 = 39 and it's mirror cell is r2c1. Because of the clue paring r2c1 can only be 7 (the clue pair of 3) or 1 (the clue pair of 9) , so 2 and 9 can be removed there.

Similarly r3c1 <> 9, r4c1 = 9 (the clue pair of the given cell r1c4 = 1) etc etc.

Proceeding in this way and applying basics I suspect that we will arrive at the post basics PM for the easier version of the puzzle, or possibly something even easier.

So an I a dunce, a DUX, or something in between ?

Leren

I think there may be a few problems with this claim. First, the cell r9c9 does not have a pair and its value can not be determined by analyzing symmetry. Also, it isn't guaranteed that r1c4 and r5c2 are mirror cells at this point in the puzzle, as the values of r4c1 and r2c5 are unknown. Once the values of r4c1 and r2c5 are established the TLBR symmetry rules should apply.

Regarding the symmetry on the other diagonal, I designed the puzzle with the intention of having this symmetry, but not with any specific method for finding it. So while I can't say for sure that there isn't a way to show the symmetry on that diagonal, I have no idea what it would be.

[pjb]

First puzzle:

Code: Select all

 4       9       3      | 1      57     568    | 578    2      68     
 1       5       8      | 467    2      69     | 47     679    3     
 7       2       6      | 48     459    3      | 1      59     489   
------------------------+----------------------+---------------------
 9       346     24     | 5      8      1      | 234    36     7     
 35      8      d145    | 2      6      7      | 9     b135   c14     
 256     16      7      | 9      3      4      | 25     8      126   
------------------------+----------------------+---------------------
 235     34      9      | 478    1      58     | 6      37     28     
 8       136    e15     | 67     579    2      | 37     4      9-1     
 26      7       24-1   | 3      49     689    | 28    a19     5     


(1)r9c8 = r5c9 - (1=5)r5c39 - (5=1)r8c3 => -1 r8c9, r9c3; lclste

Phil

[Leren]

It will be interesting to see if someone can come up with a human friendly solution to the harder puzzle. I had to use 11 brute force forcing chains. That was better than Hodoku - they used 16 and whole lot of loops and chains as well.

Leren

[gurth]

Easier version:
CW:

(abc) disproves blue - inserting red 4s plus 4r9c5 and 4r7c2 (from symmetry) -> stte.

[eleven]

The easy one:

Code: Select all

+----------------+----------------+----------------+
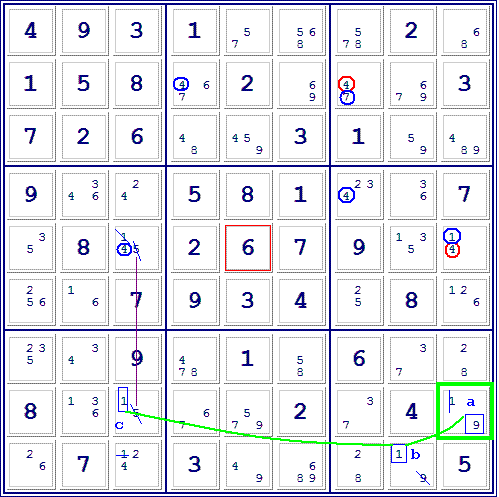
| 4    9    3    | 1    57  *568  |-578  2    68   |
| 1    5    8    | 467  2    69   | 47   679  3    |
| 7    2    6    | 48   459  3    | 1    59   489  |
+----------------+----------------+----------------+
| 9    346  24   | 5    8    1    | 234  36   7    |
| 35   8   d145  | 2    6    7    | 9    135  14   |
|*256  16   7    | 9    3    4    | 25   8    126  |
+----------------+----------------+----------------+
| 23-5 34   9    | 478  1    58   | 6    37   28   |
| 8    136  15   | 67   579  2    | 37   4    19   |
| 26   7    124  | 3    49   689  | 28   19   5    |
+----------------+----------------+----------------+

5r6c7=r6c1/r1c6 => r1c7/r7c1<>5 stte

In the minimal one it would be hard to show digital symmetry.

[blue]

The minimal puzzle can be transformed to one with 180 degree rotational symmetry, and solved that way.
This isn't very elegant (below), but it works. It's a sketch for a "T&E" solution.

Code: Select all

initial puzzle:

+-------+-------+-------+
| 4 . . | 1 . . | . 2 . |
| . 5 . | . . . | . . 3 |
| . . 6 | . . 3 | 1 . . |
+-------+-------+-------+
| . . . | 5 . . | . . 7 |
| . 8 . | . 6 . | 9 . . |
| . . 7 | . . 4 | . 8 . |
+-------+-------+-------+
| . . 9 | . 1 . | 6 . . |
| 8 . . | . . 2 | . 4 . |
| . 7 . | 3 . . | . . . |
+-------+-------+-------+


Code: Select all

transform the puzzle like this:

    swap bands 2&3 and stacks 2&3    (b5 and b9)
    swap rows 5&6 and columns 5&6    (r5c5 and r6c6)
    swap rows 7&9 and columns 7&9    (r7c7 and r9c9)
    swap rows 8&9 and columns 8&9    (r8c8 and r9c9)

+-------+-------+-------+
| 4 . . | . . 2 | . 1 . |
| . 5 . | . 3 . | . . . |
| . . 6 | 1 . . | 3 . . |
+-------+-------+-------+
| . . 9 | 6 . . | . . 1 |
| . 7 . | . . . | . 3 . |
| 8 . . | . . 4 | 2 . . |
+-------+-------+-------+
| . . 7 | . . 8 | 4 . . |
| . . . | . 7 . | . 5 . |
| . 8 . | 9 . . | . . 6 |
+-------+-------+-------+

The result has an automorphism involving a 180 degree rotation, and digit pairs (18)(29)(37)(46)
 => add 5r5c5

Code: Select all

+-----------------------+---------------+-----------------------+
| 4       39      38    | 578  689  2   | 56789  1       5789   |
| 1279    5       128   | 478  3    679 | 6789   246789  24789  |
| 279     29      6     | 1    489  579 | 3      24789   245789 |
+-----------------------+---------------+-----------------------+
| 235     234     9     | 6    28   37  | 578    478     1      |
| 126     7       124   | 28   5    19  | 689    3       489    |
| 8       136     135   | 37   19   4   | 2      679     579    |
+-----------------------+---------------+-----------------------+
| 123569  12369   7     | 235  126  8   | 4      29      239    |
| 12369   123469  1234  | 234  7    136 | 189    5       2389   |
| 1235    8       12345 | 9    124  135 | 17     27      6      |
+-----------------------+---------------+-----------------------+

4r5c3/6r5c7 leads to a contradiction (via singles)
 => add 4r4c2/6r6c8 and 4r5c9/6r5c1

Code: Select all

+---------------------+---------------+---------------------+
| 4      39     38    | 578  689  2   | 56789  1      5789  |
| 1279   5      128   | 478  3    679 | 6789   24789  2789  |
| 279    29     6     | 1    489  579 | 3      24789  25789 |
+---------------------+---------------+---------------------+
| 235    4      9     | 6    28   37  | 578    78     1     |
| 6      7      12    | 28   5    19  | 89     3      4     |
| 8      13     135   | 37   19   4   | 2      6      579   |
+---------------------+---------------+---------------------+
| 12359  12369  7     | 235  126  8   | 4      29     239   |
| 1239   12369  1234  | 234  7    136 | 189    5      2389  |
| 1235   8      12345 | 9    124  135 | 17     27     6     |
+---------------------+---------------+---------------------+

2r5c4/9r5c6 leads to a contradiction (via singles)
 => add 2r4c6/9r6c8, 2r5c3/9r5c7 and 8r5c4/1r5c6

Code: Select all

+--------------------+--------------+--------------------+
| 4      39     38   | 57   68  2   | 5678  1      5789  |
| 1279   5      18   | 47   3   679 | 678   24789  2789  |
| 279    29     6    | 1    48  579 | 3     24789  25789 |
+--------------------+--------------+--------------------+
| 35     4      9    | 6    2   37  | 578   78     1     |
| 6      7      2    | 8    5   1   | 9     3      4     |
| 8      13     135  | 37   9   4   | 2     6      57    |
+--------------------+--------------+--------------------+
| 12359  12369  7    | 235  16  8   | 4     29     239   |
| 1239   12369  134  | 234  7   36  | 18    5      2389  |
| 1235   8      1345 | 9    14  35  | 17    27     6     |
+--------------------+--------------+--------------------+

5r1c4/5r9c6 leads to a contradiction (via singles)
 => add 5r3c6/5r7c4, and finish with singles