Hi guys,
I have a couple of questions regarding sudoku coordinate systems.
1. What kind of coordinate systems are currently in use, or have been used in the past, for vanilla (9x)9x9 sudoku? On this forum we obviously use the (N)rYcX and (N)bBpP coordinates, but there are others (mostly using letters for some coordinate) in use elsewhere. Could we build a list of those for reference? (Let's assume we only use the (n)rc-space, as the transformations to other spaces only switch the ordering of the three coordinates.)
2. What kind of coordinates are used in bigger vanilla sudokus, say 16x16? The normal (N)rYcX and (N)bBpP obviously don't work very well with a set of only nine digits. How is that normally solved? I assume letters are used, too, but how exactly? (I don't play big sudokus so I don't really know.)
3. What about combined vanilla sudokus, like samurais? Obviously mere rc/bp-coordinates are no longer enough to identify a cell. (Again, I don't really play those, so I have no idea how it's done.)
4. What about variants with additional or different constraints, such as X-Sudoku, WinDoku, Killer, Jigsaw? In those (9x9) variants rYcX (and possibly bBpP) do work to identify any cell, but there are reasons to identify each constraint as well (in exotic fishing, for example). Are there any standards for those?
5. Which variants are the most relevant these days anyway? (My experience with any variants is very limited.)
PS. One reason why I'm asking is that I've created a new (?) coordinate system for my personal use. It's optimized (from my pov) for 9x9 vanillas, but it has limited potential for some variants as well. Before even attempting to extend it into those, I'd like to know what the standard ways to address their coordinates and constraints are, and also which variants are the most relevant ones to even support. I'd also like to know if the core idea of my system is already in use somewhere.
Sudoku coordinate systems?
10 posts
• Page 1 of 1
Re: Sudoku coordinate systems?
Andoku 3 on android probably has every common variation.
Certain variations like Killer and Sumdoku or other varients that have math involved usually is a seperate app just for that single varient. Killer is probably the most popular varient that needs a seperate app.
There is even apps that have greater/less than varients on top of regular varients. For example X-sudoku with a greater/less than on top of that varient.
Wish I could remember which app that was, that had that.
Certain variations like Killer and Sumdoku or other varients that have math involved usually is a seperate app just for that single varient. Killer is probably the most popular varient that needs a seperate app.
There is even apps that have greater/less than varients on top of regular varients. For example X-sudoku with a greater/less than on top of that varient.
Wish I could remember which app that was, that had that.
- Pupp
- Posts: 246
- Joined: 18 October 2019
Re: Sudoku coordinate systems?
SpAce wrote:2. What kind of coordinates are used in bigger vanilla sudokus, say 16x16? The normal (N)rYcX and (N)bBpP obviously don't work very well with a set of only nine digits. How is that normally solved? I assume letters are used, too, but how exactly?
For 16x16, there are at least 4 different systems (1-16, 0-9A-F, 1-9A-G, A-P) used for puzzle/grid presentation, so there is probably no "normal". But perhaps there should be ...
For cell identification, I would suggest that letters be avoided. (N)rYcX works perfectly well, and unambiguously, if you stick to decimal number format, eg (16)r3c12.
The letters vs numbers advantage is lost beyond 25x25, in any case.
SpAce wrote:3. What about combined vanilla sudokus, like samurais? Obviously mere rc/bp-coordinates are no longer enough to identify a cell.
You can add a grid number: eg (16)g2r3c12.
SpAce wrote:4. What about variants with additional or different constraints, such as X-Sudoku, WinDoku, Killer, Jigsaw?
5. Which variants are the most relevant these days anyway? (My experience with any variants is very limited.)
I don't think anyone has seriously considered the problem of contraint-addressing, my brain hurts just thinking about it ...
-

Mathimagics - 2017 Supporter
- Posts: 1926
- Joined: 27 May 2015
- Location: Canberra
Re: Sudoku coordinate systems?
Mathimagics wrote:You can add a grid number: eg (16)g2r3c12.SpAce wrote:3. What about combined vanilla sudokus, like samurais? Obviously mere rc/bp-coordinates are no longer enough to identify a cell.SpAce wrote:4. What about variants with additional or different constraints, such as X-Sudoku, WinDoku, Killer, Jigsaw
The subject comes right in time, being busy with the next
SiSeSuSo. I use (16)2r3c4 for candidates 1 and 6 in sudoku 2 row 3 column 4, no "g". All positions always in reading order. For boxes also (16)2b3e4 for box 3 element 4. For Asterisk I use capitals (16)2A6. We have to decide where to start the element numbering and clockwise. For diagonals (16)2D1e5 on the first and (16)2D2e7 on the second diagonal. For a windoku (16)2W3e4 and the 4 visible boxes are obvious but the order of the 5 hidden houses still to be decided.
Last edited by Hajime on Mon Jul 20, 2020 9:44 am, edited 1 time in total.
-
Hajime - Posts: 1408
- Joined: 20 April 2018
- Location: Fryslân
Re: Sudoku coordinate systems?
I use the grc system for my puzzle coordinates g: Grid r: Row c: Column which satisfies most situations. For region naming it becomes more tricky because you need a universal way of naming them.
Boxes/Blocks should be easiest with "b" (numbering is already well established as universal)
Windows also shouldn't be an issue with "w" (numbering is nearly universal & I mention this in the Welcome window in Sukaku explainer & the Brief description on the related wiki pages)
With Disjoint Groups it looks that "p" is acceptable as it stands for Box Position
Diagonals has a small issue ( "/", "\", d1, d2, d, ad, md, ...) but should be overcome through consensus
I would still use grc system for gattai although you can look at Gattais as one grid and use rc only. I would try to use the relevant g number in overlapping areas if possible followed by the smallest g number if the relevance to overlapping grids is the same.
For larger grids, as Mathimagics mentioned, There are several ways to do it ... I have over the years (For storage, sorting, etc) insisted on 1 character per symbol which then can translate into 1 character per g,r & c. My opinion (I think gsf was the same) is to name everything the same way ... This means that because we have decided to use 1-9 for symbols & rc numbering in 9x9 grids that we should expand and continue from there to larger grids. So 1-G for 16x16 for instance ... [1-9][A-Z][a-z] should cover things up to 49x49 and should be universally accepted ... Anything bigger is open for debate.
tarek
Boxes/Blocks should be easiest with "b" (numbering is already well established as universal)
Windows also shouldn't be an issue with "w" (numbering is nearly universal & I mention this in the Welcome window in Sukaku explainer & the Brief description on the related wiki pages)
With Disjoint Groups it looks that "p" is acceptable as it stands for Box Position
Diagonals has a small issue ( "/", "\", d1, d2, d, ad, md, ...) but should be overcome through consensus
I would still use grc system for gattai although you can look at Gattais as one grid and use rc only. I would try to use the relevant g number in overlapping areas if possible followed by the smallest g number if the relevance to overlapping grids is the same.
For larger grids, as Mathimagics mentioned, There are several ways to do it ... I have over the years (For storage, sorting, etc) insisted on 1 character per symbol which then can translate into 1 character per g,r & c. My opinion (I think gsf was the same) is to name everything the same way ... This means that because we have decided to use 1-9 for symbols & rc numbering in 9x9 grids that we should expand and continue from there to larger grids. So 1-G for 16x16 for instance ... [1-9][A-Z][a-z] should cover things up to 49x49 and should be universally accepted ... Anything bigger is open for debate.
tarek
Last edited by tarek on Mon Jul 20, 2020 9:56 am, edited 1 time in total.
-

tarek - Posts: 3762
- Joined: 05 January 2006
Re: Sudoku coordinate systems?
Looks like a can of worms has been opened. As there is no standards, I tend to go with what is easiest to program!
0. I use (prefer) lower case representation. I've seen upper case used elsewhere.
1. I use (N)rYcX and used (N)bBoO, (O)ffset but now also use (N)bBiI, (I)ndex. I tend not to use the A-I1-9 notation, as A-I are rows at sudokuwiki, and A-I are columns in SudokuExplainer!
2. For 16x16 puzzles, I use (N)rYcX where NYX are numbers 1-16 as in Sudoku16x16Explainer. For saving I use cell values A-P (single char). Mathimagics has mentioned the other systems in current use!
3. For gattais, I use (N)gNrYcX, where (G)rid numbering is from top-left to bottom-right in grid r1c1 order. For samurais, g=1-5 works well enough. For bigger gattais, less so, e.g. g67r6c7 in an 85-grids DOAG.
4a. Windoku: (N)wNiI, where windokus have 9 contraints and I know of 2 different windoku numbering order! One is the top-left to bottom-right order. I use the (4) 3x3s, (2) 1x3s, (2) 3x1s and (1) 1x1 order!!
4a. Jigsaw: (N)cNiI, (C)age numbering is from top-left to bottom-right in cage first cell order. For cage definition strings I use 1-9, rather than 0-8.
In SukakuExplainer, an example hint might be:
Hidden Single: r3c7: 4 in Asterisk group
when other groups can be Window (Windoku), Disjoint, Main Diagonal, Anti Diagonal, Girandola, Center Dot.
These identify the technique used, e,g,
Hidden Single: r3c4: 5 in row
Hidden Single: r4c6: 7 in column
Hidden Single: r5c8: 9 in block
Edit: Any system that requires a second conversion (mental or otherwise) for representation or visualization is likely doomed!
0. I use (prefer) lower case representation. I've seen upper case used elsewhere.
1. I use (N)rYcX and used (N)bBoO, (O)ffset but now also use (N)bBiI, (I)ndex. I tend not to use the A-I1-9 notation, as A-I are rows at sudokuwiki, and A-I are columns in SudokuExplainer!
2. For 16x16 puzzles, I use (N)rYcX where NYX are numbers 1-16 as in Sudoku16x16Explainer. For saving I use cell values A-P (single char). Mathimagics has mentioned the other systems in current use!
3. For gattais, I use (N)gNrYcX, where (G)rid numbering is from top-left to bottom-right in grid r1c1 order. For samurais, g=1-5 works well enough. For bigger gattais, less so, e.g. g67r6c7 in an 85-grids DOAG.
4a. Windoku: (N)wNiI, where windokus have 9 contraints and I know of 2 different windoku numbering order! One is the top-left to bottom-right order. I use the (4) 3x3s, (2) 1x3s, (2) 3x1s and (1) 1x1 order!!
4a. Jigsaw: (N)cNiI, (C)age numbering is from top-left to bottom-right in cage first cell order. For cage definition strings I use 1-9, rather than 0-8.
In SukakuExplainer, an example hint might be:
Hidden Single: r3c7: 4 in Asterisk group
when other groups can be Window (Windoku), Disjoint, Main Diagonal, Anti Diagonal, Girandola, Center Dot.
These identify the technique used, e,g,
Hidden Single: r3c4: 5 in row
Hidden Single: r4c6: 7 in column
Hidden Single: r5c8: 9 in block
Edit: Any system that requires a second conversion (mental or otherwise) for representation or visualization is likely doomed!
-

1to9only - Posts: 4211
- Joined: 04 April 2018
Re: Sudoku coordinate systems?
In my solver is use NrYcX and constraintindex. Which is in the context of current puzzle. Grid or constraint naming can be useful for a manual solver. For a generic solver more constraints are possible and then the solver has no name for it.
Like a windoku, how do you call the hidden 5 boxes?
How do you call double windoku (offsets r1c1 and r2c2)?
Best way is just to visualize it for the user.
My generic solver is maybe not handy if you have different ratings for different constraints.
Parsing should be not a big problem.
For notations it could reduce the amount of text. For example row 12r23c4 and for box 1r1c1,1r2c2 could be 1b1.
And I think it would be mainly used for sharing on the forum.
Like a windoku, how do you call the hidden 5 boxes?
How do you call double windoku (offsets r1c1 and r2c2)?
Best way is just to visualize it for the user.
My generic solver is maybe not handy if you have different ratings for different constraints.
Parsing should be not a big problem.
For notations it could reduce the amount of text. For example row 12r23c4 and for box 1r1c1,1r2c2 could be 1b1.
And I think it would be mainly used for sharing on the forum.
- creint
- Posts: 402
- Joined: 20 January 2018
Re: Sudoku coordinate systems?
I must say that the notation system I mentioned above is what I would use in a helper program "Hint window".
With programming it is different as it is all numbered starting from 0
tarek
With programming it is different as it is all numbered starting from 0
tarek
-

tarek - Posts: 3762
- Joined: 05 January 2006
Re: Sudoku coordinate systems?
The issue with Sudoku and why there isn't a standard format moves is because unlike most games, the board size is fungible.
9x9 is the basic standard, but puzzles for children are often much smaller, then there are puzzles that are essentially overlapping Samuri puzzle. SudoCue has Clueless Specials and Clueless Explosion for examples.
sudocue.net
9x9 is the basic standard, but puzzles for children are often much smaller, then there are puzzles that are essentially overlapping Samuri puzzle. SudoCue has Clueless Specials and Clueless Explosion for examples.
sudocue.net
- Pupp
- Posts: 246
- Joined: 18 October 2019
Re: Sudoku coordinate systems?
Thanks a lot for the great answers, everyone! I really appreciate it. I've already learned a lot, like that Windoku has 9 extra constraints instead of the obvious 4!  It pretty much means that it probably can't be supported by my new system, unlike I originally thought.
It pretty much means that it probably can't be supported by my new system, unlike I originally thought.
In any case, it's obvious that the NgGrYcX is the most generally applicable coordinate system, and it would be nice to standardize it as much as possible. I'm willing to work on that too, if there's interest. My new system is not meant to replace it at all, and it's not capable of it either. It's just a shortcut for the most common addressing needs, especially for the vanilla (9x)9x9 sudoku. One goal is to shorten the chains, fishes, and matrices we use in the Puzzles section, as the NrYcX-coordinates take a lot of space and in some ways hinder readability as well. (Note that I still think that those coordinates are the most intuitive to understand, which is another reason to keep them as the main standard.)
My system will never work for anything bigger than (9x)9x9, so variants like (16x)16x16 are for sure out of its league. It might work for some gattais with 9x9 subgrids, but I haven't really thought about it (it would need a standard way to address the g-coordinate). It could work for some 9x9 variants with few extra constraints, such as Sudoku-X and Asterisk. It might work with 9x9 Killers and Jigsaws, but I haven't put much thought into that either. For basic cell addressing it works for any 9x9 grid (or smaller), but my wish to have a consistent way to address the extra constraints (for fishing) and even their cells (for subsets) limits its full applicability, unless some non-confusing escape mechanism is built into it. All of these are open questions at the moment.
Let me introduce my proposed system at this point, so you know what I'm talking about. Also, if someone recognizes it as an already existing system, please let me know. Otherwise it probably needs a name so it can be referred to. My working title for it is 19aIrZ, which pretty much describes it as well. (That's a capital-i in case the font makes it look like a lowercase-L or a 1 -- a known problem, though less severe in practice because of other design choices). It's obviously very close to existing systems that use letters for coordinates, but I'm not sure if any exist with the exact same idea.
The idea is that every coordinate in a vanilla sudoku (n, r, c, b, p) has its own set of nine symbols that can't be confused with each other, making it possible to refer to them with a single symbol. It shortens both chains and fishes (including generic truths and links) considerably, and makes matrices much more compact. Another goal is that contrast should be maximized by placing symbols of different sizes next to each other, unless they belong to the same set. It means that digits and uppercase letters, or two lower-/uppercase letters, shouldn't normally be adjacent (some exceptions allowed, as in fishes or if solving in alternate spaces, but in those cases some separators should be considered to enhance readability). That way non-required brackets or other separators can be mostly avoided while still maintaining reasonable readability, which further shortens chains etc. The chosen symbols are:
The normal ordering for cell or subset coordinates is:
And for (single-digit) fishes:
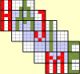
In other words, (3)r4c8 would be 3dH, and (7)b5p6 would be 7vW. Groups and subsets work normally: (6)r23c7 is 6bcG, (123)r1c689 is 123aFHI, (4567)b2p1389 is 4567sRTYZ. Fishes work too: Swordfish (3)c479\r158 is 3{DGI\aeh}, and Finned Mutant X-Wing (2-String Kite) (5)r1c5\r7c1b2 is 5{aE\gAs}. Fishing is one reason why I chose separate letters for the boxes, even though it complicates things a little bit.
As for truths and links (or what I call Alien Fishes), Allan Barker's idea of using uppercase for truths and lowercase for links must obviously be dropped with these coordinates (those roles should be obvious anyway, so it's a pretty redundant convention in the first place). Here's the Easter Monster SK-Loop expressed as an "Alien Fish" using this system: {bhACGI acgiBH \ 38b 45h 48.B 39H 27rz 16tx}. Normally it would be {28N1379 1379N28 \ 38r2 45r8 48c2 39c8 27b19 16b37}. It's not that much shorter but it avoids the annoyingly unintuitive N-syntax for cell sets.
So, that's the basic idea. For those used to the (N)rYcX-coordinates (myself included), it takes a while to get used to, but not as much as I thought. It's actually quite convenient in practice. My choice of the first and the last nine letters in the alphabet should make it easy to remember, even though other choices (like using J or K instead of I) might be more readable. If it proves problematic in practice, that choice could be revisited. I think the problem is mostly avoided with the adjacency rule, but as we've seen, there are exceptions when it can't be followed. Another problem is B vs 8 if they have to be adjacent, as in that Alien Fish above (hence the dot between them).
There are still eight letters left (j k l m n o p q) in the alphabet, so 2x8 symbols available to use for extra coordinates in variants, if one wishes (though I would definitely avoid the lowercase-L). Of course every addition makes things more complicated, so I'm not sure how good of an idea it is. Sudoku-X seems like the most viable candidate because it only has two extra constraints. If they were assigned p and q, for example, then each of their nine cells could be addressed by using the same position letters (R..Z) as for boxes. In other words, (2)d1p6 (r6c6) would be 2pW, and (2)d2p3 (r7c3) would be 2qT. Of course, the real benefit is when using diagonal-based subsets or fishes.
Any thoughts?
Added. An example.
In any case, it's obvious that the NgGrYcX is the most generally applicable coordinate system, and it would be nice to standardize it as much as possible. I'm willing to work on that too, if there's interest. My new system is not meant to replace it at all, and it's not capable of it either. It's just a shortcut for the most common addressing needs, especially for the vanilla (9x)9x9 sudoku. One goal is to shorten the chains, fishes, and matrices we use in the Puzzles section, as the NrYcX-coordinates take a lot of space and in some ways hinder readability as well. (Note that I still think that those coordinates are the most intuitive to understand, which is another reason to keep them as the main standard.)
My system will never work for anything bigger than (9x)9x9, so variants like (16x)16x16 are for sure out of its league. It might work for some gattais with 9x9 subgrids, but I haven't really thought about it (it would need a standard way to address the g-coordinate). It could work for some 9x9 variants with few extra constraints, such as Sudoku-X and Asterisk. It might work with 9x9 Killers and Jigsaws, but I haven't put much thought into that either. For basic cell addressing it works for any 9x9 grid (or smaller), but my wish to have a consistent way to address the extra constraints (for fishing) and even their cells (for subsets) limits its full applicability, unless some non-confusing escape mechanism is built into it. All of these are open questions at the moment.
Let me introduce my proposed system at this point, so you know what I'm talking about. Also, if someone recognizes it as an already existing system, please let me know. Otherwise it probably needs a name so it can be referred to. My working title for it is 19aIrZ, which pretty much describes it as well. (That's a capital-i in case the font makes it look like a lowercase-L or a 1 -- a known problem, though less severe in practice because of other design choices). It's obviously very close to existing systems that use letters for coordinates, but I'm not sure if any exist with the exact same idea.
The idea is that every coordinate in a vanilla sudoku (n, r, c, b, p) has its own set of nine symbols that can't be confused with each other, making it possible to refer to them with a single symbol. It shortens both chains and fishes (including generic truths and links) considerably, and makes matrices much more compact. Another goal is that contrast should be maximized by placing symbols of different sizes next to each other, unless they belong to the same set. It means that digits and uppercase letters, or two lower-/uppercase letters, shouldn't normally be adjacent (some exceptions allowed, as in fishes or if solving in alternate spaces, but in those cases some separators should be considered to enhance readability). That way non-required brackets or other separators can be mostly avoided while still maintaining reasonable readability, which further shortens chains etc. The chosen symbols are:
- Code: Select all
n: 1 2 3 4 5 6 7 8 9
r: a b c d e f g h i
c: A B C D E F G H I
b: r s t u v w x y z
p: R S T U V W X Y Z
The normal ordering for cell or subset coordinates is:
- Code: Select all
NrC or NbP
And for (single-digit) fishes:
- Code: Select all
N{rCb\rCb}
In other words, (3)r4c8 would be 3dH, and (7)b5p6 would be 7vW. Groups and subsets work normally: (6)r23c7 is 6bcG, (123)r1c689 is 123aFHI, (4567)b2p1389 is 4567sRTYZ. Fishes work too: Swordfish (3)c479\r158 is 3{DGI\aeh}, and Finned Mutant X-Wing (2-String Kite) (5)r1c5\r7c1b2 is 5{aE\gAs}. Fishing is one reason why I chose separate letters for the boxes, even though it complicates things a little bit.
As for truths and links (or what I call Alien Fishes), Allan Barker's idea of using uppercase for truths and lowercase for links must obviously be dropped with these coordinates (those roles should be obvious anyway, so it's a pretty redundant convention in the first place). Here's the Easter Monster SK-Loop expressed as an "Alien Fish" using this system: {bhACGI acgiBH \ 38b 45h 48.B 39H 27rz 16tx}. Normally it would be {28N1379 1379N28 \ 38r2 45r8 48c2 39c8 27b19 16b37}. It's not that much shorter but it avoids the annoyingly unintuitive N-syntax for cell sets.
So, that's the basic idea. For those used to the (N)rYcX-coordinates (myself included), it takes a while to get used to, but not as much as I thought. It's actually quite convenient in practice. My choice of the first and the last nine letters in the alphabet should make it easy to remember, even though other choices (like using J or K instead of I) might be more readable. If it proves problematic in practice, that choice could be revisited. I think the problem is mostly avoided with the adjacency rule, but as we've seen, there are exceptions when it can't be followed. Another problem is B vs 8 if they have to be adjacent, as in that Alien Fish above (hence the dot between them).
There are still eight letters left (j k l m n o p q) in the alphabet, so 2x8 symbols available to use for extra coordinates in variants, if one wishes (though I would definitely avoid the lowercase-L). Of course every addition makes things more complicated, so I'm not sure how good of an idea it is. Sudoku-X seems like the most viable candidate because it only has two extra constraints. If they were assigned p and q, for example, then each of their nine cells could be addressed by using the same position letters (R..Z) as for boxes. In other words, (2)d1p6 (r6c6) would be 2pW, and (2)d2p3 (r7c3) would be 2qT. Of course, the real benefit is when using diagonal-based subsets or fishes.
Any thoughts?
Added. An example.
-

SpAce - Posts: 2671
- Joined: 22 May 2017
10 posts
• Page 1 of 1

