The New Sudoku Players' Forum

[RoseWillow]

Here is the original puzzle:

Code: Select all

 *-----------*
 |...|.64|..9|
 |.1.|8..|...|
 |5..|7..|.28|
 |---+---+---|
 |..6|4..|7.5|
 |...|...|...|
 |7.3|..1|9..|
 |---+---+---|
 |19.|..2|..6|
 |...|..8|.7.|
 |2..|64.|...|
 *-----------*

and here is where I am stuck:

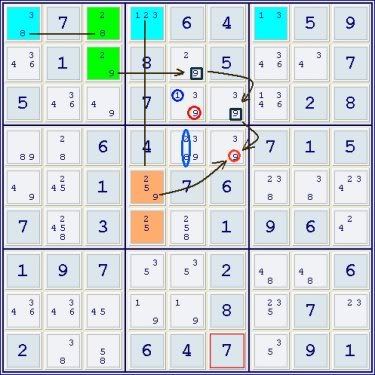
Code: Select all

38    7      28   | 123   6      4     | 13    5      9
346   1      29   | 8     29     5     | 346   34     7
5     346    49   | 7     139    39    | 1346  2      8
------------------+--------------------+-------------------
89    28     6    | 4     2389   39    | 7     1      5
49    245    1    | 259   7      6     | 238   38     234
7     2458   3    | 25    258    1     | 9     6      24
------------------+--------------------+-------------------
1     9      7    | 35    35     2     | 48    48     6
346   346    45   | 19    19     8     | 235   7      23
2     38     58   | 6     4      7     | 35    9      1

I can't see any regular fish (there may be sashimi, mutant or franken fish that I can't see, I'm not good with fish), xy-wings, xyz-wings, gordonian rectangles, chains, bilocation cycles or bivalue graphs. Obviously I'm not seeing *something*, I just can't figure out what it is.

Please help? The author (Frank Longo) says that every puzzle in the book is fair, with no guessing required, so there must be SOMEthing in there that I'm just not seeing.

I'm new to the forum, and I don't understand the notation that is used around the Sudoku forums on the internet, so if you use such notation, please explain it, or you won't be doing me any good at all. (Obviously I do understand row/column stuff -- r1c2 or whatever.)

Thanks!

-Rose

[daj95376]

Of the possible steps, I'd put my $$$ on the author expecting you to find:

Code: Select all

         XYZ-Wing [r3c5]/[r3c6]+[r8c5]   <> 9    [r2c5]


[aran]

Rose Willow
Another viewpoint for you.
Look at r3c5 and r3c6
If r3c5 is not 1, then those cells form a pair 39, so r3c3 would be 4
If r3c5 is 1, then r8c5=9, r2c5=2, r2c3=9, so r3c3 would also be 4.
Since r3c5 must either be 1 or not 1, and since under both options r3c3 is 4, we have a verdict that cannot be contested.
(this way of looking at things is called "hidden set" logic).

[Luke]

Rose Willow, very nice job presenting your puzzle for a first time poster (...here, anyways.)

I'm not betting against Danny's suggestion as to the author's intention. I am betting that you'll like using w-wings, though. Look for identical bivalue cells not in the same house, like these two with (38).

Code: Select all

 *-----------------------------------------------------------*
 |*38    7     28    | 123   6     4     | 13    5     9     |
 | 346   1     29    | 8     29    5     | 346   34    7     |
 | 5    -346   49    | 7     139   39    | 1346  2     8     |
 |-------------------+-------------------+-------------------|
 | 89    28    6     | 4     2389  39    | 7     1     5     |
 | 49    245   1     | 259   7     6     | 238   38    234   |
 | 7     2458  3     | 25    258   1     | 9     6     24    |
 |-------------------+-------------------+-------------------|
 | 1     9     7     | 35    35    2     | 48    48    6     |
 |-346   346   45    | 19    19    8     | 235   7     23    |
 | 2    *38    58    | 6     4     7     | 35    9     1     |
 *-----------------------------------------------------------*


When you have this setup, look for a strong link on either value (3 or 8) that can see both the bivalue cells, but doesn't touch either. In this case, the two 8's in column 3 fill the bill. This means that any 3 that can see both your bivalue cells can be eliminated. The idea is that since at least one of the conjugate 8's must be true, then one of the 3's must also be true.

With the two 3's out of the way, there's another w-wing on (46) that solves the puzzle. Can you see it?

Code: Select all

 *-----------------------------------------------------------*
 | 38    7     28    | 123   6     4     | 13    5     9     |
 | 346   1     29    | 8     29    5     | 346   34    7     |
 | 5    *46    49    | 7     139   39    | 1346  2     8     |
 |-------------------+-------------------+-------------------|
 | 89    28    6     | 4     2389  39    | 7     1     5     |
 | 49    245   1     | 259   7     6     | 238   38    234   |
 | 7     2458  3     | 25    258   1     | 9     6     24    |
 |-------------------+-------------------+-------------------|
 | 1     9     7     | 35    35    2     | 48    48    6     |
 |*46    346   45    | 19    19    8     | 235   7     23    |
 | 2     38    58    | 6     4     7     | 35    9     1     |
 *-----------------------------------------------------------*

[RoseWillow]

Thank you Daj, Aran and Luke.

I should have seen that xyz-wing! I stared at it for hours! (off and on)

Luke, very cool logic on the w-wing. I hadn't seen that explained -- maybe I haven't read deeply enough on the wiki. Anyway. Is it r3c3 and r8c3 with candidate 4? (What do you mean by "doesn't touch"?) That means 6 can be removed from r2c1 and r8c2. That doesn't solve it right away for me (like the xyz-wing and the hidden set logic does, both of which make the rest of the puzzle solve like a stack of dominos). Would you mind continuing with your logic? (I'd like to learn from it.)

[Luke]

Rose Willow, you're right, the w-wings don't solve the puzzle. I saw some singles coming, but the xyz-wing is still the way home.

You're also right with the (46) w-wing. By "doesn't touch" I meant that neither of the bivalue cells should be part of the strong link. For example, in the (46) wing there is a strong link with the conjugate 6's in column two that can't be used for a w-wing.

[Draco]

Another path that breaks the puzzle to STE is this simple forcing chain:

Code: Select all

38  7    28 | 123 6    4  | 13   5  9 
346 1    29 | 8   29   5  | 346  34 7 
5   346  49 | 7   139  39 | 1346 2  8 
------------+-------------+------------
89  28   6  | 4   2389 39 | 7    1  5 
49  245  1  | 259 7    6  | 238  38 234
7   2458 3  | 25  258  1  | 9    6  24
------------+-------------+------------
1   9    7  | 35  35   2  | 48   48 6 
346 346  45 | 19  19   8  | 235  7  23
2   38   58 | 6   4    7  | 35   9  1

r1c4=1 r2c5=2 and
r3c5=1 r8c5=9 mean that r2c5<>9

Forcing chains rely on bi-value or bi-local starting points (in this case, the paired 1's in r1c4 and r3c5). Since one of these 1's must be part of the solution, any values that are eliminated by choosing either as true (in this case, following a short "cascade" of singles forced by each starting value) may be safely excluded from the puzzle.

Since the first path explicitly sets r2c5 to something other than 9 and the second sets a 9 elsewhere in col 5, we can safely eliminate 9 from r2c5. This leaves the puzzle with only singles to solve.

Chains such as these are harder to spot than the patterns mentioned by Luke, Aran and Daj. There are several good references on how to go about looking for them. Personally I have trouble spotting anything more complex than an X-Wing by eye, and use the solver I wrote for breaking tougher puzzles. This forum is also graced by several, unbelievably good people who crack much tougher puzzles strictly by hand. So don't let my reliance on my solver discourage you!

Cheers...

- drac

[DonM]

Here's another take. This puzzle appears to be at about the level of difficulty of the more difficult newspaper diabolicals, most of which can be solved by pure pattern solving or close to it.



The type 1 to 4 Unique Rectangles (http://www.brainbashers.com/sudokuuniquerectangles.asp) are relatively easily recognized patterns. Note the potential unique rectangle (39) in r34c56. It fits that of a Type 3, but here we don't need to use it as such- basic logic works: The deadly pattern, 39 in all 4 of those cells, cannot be allowed to occur so either r4c5=28 or r3c5=1 must be true:
If r4c5=28 then r4c5<>3->r4c6=3->r3c6=9 and r3c5<>9
If r3c5=1 then r3c5<>9

Either way, r3c5<>9, and can be eliminated.

ALS Chains are a powerful pattern-solving method that provides the power of the more advanced chains and yet, all you need to be able to do is recognize the patterns: http://forum.enjoysudoku.com/viewtopic.php?t=6443

Above is a 3-set ALS Chain. This was found by looking for the patterns and not by following any underlying logic. (It's good to understand the underlying logic, but nice to know that you can do some powerful solving without understanding all of it yet.) This can be a lot of fun and is particularly practical if you use the free solver, Simple Sudoku as a front end since it allows you to color cells (the above grid is from Simple Sudoku). ALS sets are those with N+1 digit values in N cells.

So, above, the Green Set (2,8,9 in 2 cells) 'connects' with the Blue Set (1,2,3,8 in 3 cells) because they both see each other's digit 8. Likewise the Blue Set sees digit 2 of the Brown Set (2,5,9 in 2 cells). So we have a chain of Green->Blue->Brown. Now note that the flanking sets, Blue and Brown both see the 9 at r3c6, the Brown set directly and the Green set indirectly thru the conjugate link of 9s in box 2 (follow the black arrows), which was made possible by our previous elimination of r3c5<>9. This means that r4c6<>9 and the puzzle is solved.

Proving this chain is relatively simple: r3c3 must be 2 or 8.
If it is 2 then r2c3=9 -> r2c5<>9 -> r3c6=9 and r4c6<>9.
If it is 8 then r1c1=3 -> r1c4=2 -> r6c4=5 -> r5c4=9 and r4c6<>9
Either way r4c6<>9 so r4c6<>9