This puzzle had what to me was an interesting one.
Ruud's Nightmare Wed Nov 21 2007
- Code: Select all
085007000000030040040102600800000501000000000207000008004608030090070000000300790
*-----------------------------------------------------------*
| 69 8 5 | 49 46 7 | 23 1 23 |
| 167 16 2 |*589 3 *569 | 89 4 57 |
| 79 4 3 | 1 58 2 | 6 58 79 |
|-------------------+-------------------+-------------------|
| 8 36 9 | 47 246 346 | 5 27 1 |
| 4 156 16 | 78 28 156 | 39 27 39 |
| 2 135 7 |*59 15 *1359 | 4 6 8 |
|-------------------+-------------------+-------------------|
| 157 7 4 | 6 9 8 | 12 3 25 |
| 3 9 16 | 2 7 145 | 18 58 46 |
| 156 2 8 | 3 145 145 | 7 9 46 |
*-----------------------------------------------------------*
This starts out as a UR on 59 but I'm trying to figure out if there's something a little more here. This pattern is one of those "strong elbows" on one base candidate and an additional strong link on the other.
Thumbnail
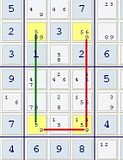
Whenever this pattern exists, the base candidate not involved with the elbow cannot be in the elbow cell. Thus r6c6 <> 5. This is pretty straight forward, altho I've never seen this particular pattern identified outside of this forum.
Let's say you didn't notice this. Instead, you decided to try 5 and 9 in the rectangle in cells where they're not involved with the strong links. For example, if 5 was in r2c6, then the strong links would force this result to avoid the Deadly Pattern:
- Code: Select all
8|5
5|9
Well, glory be, there's already a 58 in r3c5, so that's three cells for two candidates. I'm lousy at math, but this seems to add up to r2c6<>5.
Now let's say you didn't do that either. Here's a third scenario. If 9 was in r2c4 the strong links would force this result to avoid the DP:
- Code: Select all
9|6
5|9
This time, r1c45 form a triple on 469 and with the 9|6 there's four cells for three candidates. r2c4<>9, right?
My question is, can I make all three eliminations legitimately? My cake and eat it too? The latter two depend on the threat of a deadly pattern, which evaporates if scenario one is exercised first.

