The New Sudoku Players' Forum

by **SteveG48** » Sat Aug 27, 2022 5:32 pm

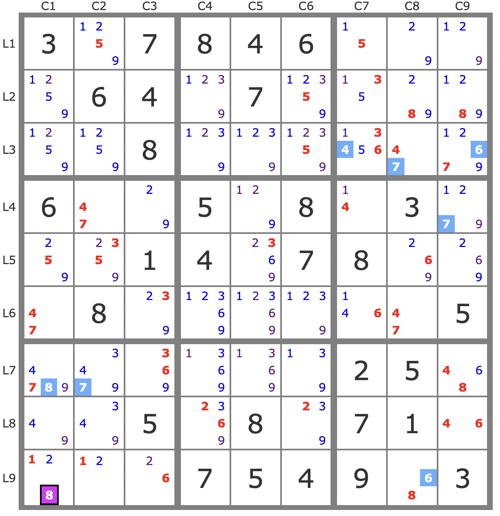
OK, here's the first in the series. Let's see how it goes.

Code: Select all: *-----------* |3.7|846|...| |.64|.7.|...| |..8|...|...| |---+---+---| |6..|...|.3.| |..1|4.7|8..| |.8.|...|..5| |---+---+---| |...|...|2..| |...|.8.|71.| |...|754|9.3| *-----------*

by **jco** » Sat Aug 27, 2022 6:33 pm

After nice "47" basics

Code: Select all: .--------------------------------------------------------------------. | 3 129 7 | 8 4 6 | 5 29 129 | | 1259 6 4 | 129 7 1259 | 3 289 1289 | | 1259 1259 8 | 1239 1239 12359 | 46 47 67 | |----------------------+----------------------+----------------------| | 6 b47 29 | 5 129 8 |c14 3 279 | | 259 2359 1 | 4 2369 7 | 8 d269 269 | | 47 8 239 | 12369 12369 1239 |c16 47 5 | |----------------------+----------------------+----------------------| | 478 a47 369 | 1369 1369 139 | 2 5 8-4 | | 49 39 5 | 2369 8 239 | 7 1 f46 | | 128 12 26 | 7 5 4 | 9 e68 3 | '--------------------------------------------------------------------'

1. (4)r7c2 = (4)r4c2 - (4=16)r46c7 - (6)r5c8 = (6)r9c8 - (6=4)r8c9 => -4 r7c9; ste

by **Mauriès Robert** » Sat Aug 27, 2022 7:02 pm

Hi all,
Here is my one-step resolution with TDP:

(-8r9c1)->8r7c1->7r7c2->7r4c9->7r3c8->4r3c7->6r3c9->6r9c8->... => -8r9c8 => r9c8=6, stte.

Hidden Text: Show

Robert

by **RSW** » Sat Aug 27, 2022 7:14 pm

Code: Select all: +---------------+-------------------+--------------+ | 3 129 7 | 8 4 6 | 5 29 129 | | 1259 6 4 | 129 7 1259 | 3 289 1289 | | 1259 1259 8 | 1239 1239 12359 | 46 c47 b67 | +---------------+-------------------+--------------+ | 6 47 29 | 5 129 8 | 14 3 279 | | 259 2359 1 | 4 2369 7 | 8 269 269 | |e47 8 239 | 12369 12369 1239 | 16 d47 5 | +---------------+-------------------+--------------+ | 478 47 369 | 1369 1369 139 | 2 5 48 | |*9-4 39 5 | 2369 8 239 | 7 1 a46 | | 128 12 26 | 7 5 4 | 9 68 3 | +---------------+-------------------+--------------+

(4=6)r8c9 - (6=7)r3c9 - (7=4)r3c8 - (4)r6c8 = (4)r6c1 => -4r8c1; stte

by **Cenoman** » Sat Aug 27, 2022 7:55 pm

Code: Select all: +----------------------+--------------------------+--------------------+ | 3 129 7 | 8 4 6 | 5 29 129 | | 1259 6 4 | 129 7 1259 | 3 289 1289 | | 1259 1259 8 | 1239 1239 12359 | 46 47 67 | +----------------------+--------------------------+--------------------+ | 6 47 29 | 5 129 8 | d14 3 279 | | 259 2359 1 | 4 2369 7 | 8 29-6 269 | | c47 8 239 | 12369 12369 1239 | d16 d47 5 | +----------------------+--------------------------+--------------------+ | c478 47 369 | 1369 1369 139 | 2 5 48 | | 49 39 5 | 2369 8 239 | 7 1 46 | | b128 12 26 | 7 5 4 | 9 a68 3 | +----------------------+--------------------------+--------------------+

(6=8)rc8 - r9c1 = (87)r67c1 - (7=146)b6p178 => -6 r5c8; ste

by **Leren** » Sat Aug 27, 2022 8:51 pm

Code: Select all: *---------------------------------------------------* | 3 129 7 | 8 4 6 | 5 29 129 | | 1259 6 4 | 129 7 1259 | 3 289 1289 | | 1259 1259 8 | 1239 1239 12359 | 46 47 a67 | |---------------+-------------------+---------------| | 6 47 29 | 5 129 8 | 14 3 b279 | | 259 2359 1 | 4 2369 7 | 8 269 269 | |d47 8 239 | 12369 12369 1239 | 16 c47 5 | |---------------+-------------------+---------------| | 478 47 369 | 1369 1369 139 | 2 5 48 | |e49 39 5 | 2369 8 239 | 7 1 4-6 | | 128 12 26 | 7 5 4 | 9 68 3 | *---------------------------------------------------*

(6=7) r3c9 - r4c9 = r6c8 - (7=4) r6c1 - r8c1 = (4) r8c9 => - 6 r8c9; stte

Leren

Website · by **denis_berthier** » Sun Aug 28, 2022 6:55 am

.

Code: Select all: Resolution state after Singles and whips[1]: +-------------------+-------------------+-------------------+ ! 3 1259 7 ! 8 4 6 ! 15 29 129 ! ! 1259 6 4 ! 1239 7 12359 ! 135 289 1289 ! ! 1259 1259 8 ! 1239 1239 12359 ! 13456 24679 12679 ! +-------------------+-------------------+-------------------+ ! 6 2479 29 ! 5 129 8 ! 14 3 1279 ! ! 259 2359 1 ! 4 2369 7 ! 8 269 269 ! ! 2479 8 239 ! 12369 12369 1239 ! 146 24679 5 ! +-------------------+-------------------+-------------------+ ! 4789 3479 369 ! 1369 1369 139 ! 2 5 468 ! ! 49 349 5 ! 2369 8 239 ! 7 1 46 ! ! 128 12 26 ! 7 5 4 ! 9 68 3 ! +-------------------+-------------------+-------------------+ 179 candidates.

1) Easy simplest-first solution:

Code: Select all: hidden-pairs-in-a-block: b4{n4 n7}{r4c2 r6c1} ==> r6c1≠9, r6c1≠2, r4c2≠9, r4c2≠2 hidden-pairs-in-a-column: c8{n4 n7}{r3 r6} ==> r6c8≠9, r6c8≠6, r6c8≠2, r3c8≠9, r3c8≠6, r3c8≠2 naked-pairs-in-a-row: r6{c1 c8}{n4 n7} ==> r6c7≠4 finned-x-wing-in-rows: n3{r5 r8}{c2 c5} ==> r7c5≠3 hidden-triplets-in-a-row: r7{n4 n7 n8}{c9 c2 c1} ==> r7c9≠6, r7c2≠9, r7c2≠3, r7c1≠9 naked-pairs-in-a-column: c2{r4 r7}{n4 n7} ==> r8c2≠4 hidden-triplets-in-a-row: r3{n4 n6 n7}{c8 c7 c9} ==> r3c9≠9, r3c9≠2, r3c9≠1, r3c7≠5, r3c7≠3, r3c7≠1 hidden-single-in-a-block ==> r2c7=3 hidden-single-in-a-block ==> r1c7=5 whip[1]: c7n1{r6 .} ==> r4c9≠1 whip[3]: c8n6{r5 r9} - r9c3{n6 n2} - b4n2{r4c3 .} ==> r5c8≠2 whip[1]: b6n2{r5c9 .} ==> r1c9≠2, r2c9≠2 biv-chain[4]: r8c9{n4 n6} - b3n6{r3c9 r3c7} - c7n4{r3 r4} - c2n4{r4 r7} ==> r7c9≠4, r8c1≠4 stte

2) 1-step solutions with no preliminary Subsets (that would eliminate half of the candidates). There are 4 possibilities in W6:

Code: Select all: whip[6]: c1n7{r7 r6} - c8n7{r6 r3} - r3n4{c8 c7} - r3n6{c7 c9} - r8c9{n6 n4} - c1n4{r8 .} ==> r7c1≠8 stte

OR:

Code: Select all: whip[6]: r7n8{c9 c1} - c1n7{r7 r6} - c8n7{r6 r3} - r3n4{c8 c7} - r3n6{c7 c9} - r8c9{n6 .} ==> r7c9≠4 stte

OR:

Code: Select all: whip[6]: r9c8{n6 n8} - r7n8{c9 c1} - c1n7{r7 r6} - c8n7{r6 r3} - r3n6{c8 c7} - r3n4{c7 .} ==> r8c9≠6 stte

OR:

Code: Select all: whip[6]: r7n8{c9 c1} - c1n7{r7 r6} - c8n7{r6 r3} - r3n4{c8 c7} - r3n6{c7 c9} - b9n6{r7c9 .} ==> r9c8≠8 stte

Steve Hodoku 8-27-2022