http://forum.enjoysudoku.com/viewtopic.php?t=6563&sid=b76053b73269ac68ba9399c670c7dc08
In this solution of Extreme #122, what is particularly interesting is that the opening chain using an aSDC, provides an elimination which makes possible the directly following chain which provides the elimination which exposes the full SDC. All of the chains which follow the SDC and, of course, solve the puzzle depend directly or indirectly on the eliminations produced by the full SDC pattern. (As usual, this is only one of what are several possible solutions.)
Extreme #122 ER=7.3 SSTS position:
- Code: Select all
*--------------------------------------------------------------------*
| 158 1478 2 | 48 58 3 | 14589 45789 6 |
| 6 3 1458 | 9 7 458 | 1458 2 15 |
| 9 478 4578 | 2 6 1 | 3458 34578 357 |
|----------------------+----------------------+----------------------|
| 7 1289 6 | 3 258 589 | 1259 59 4 |
| 1358 1289 13589 | 6 4 89 | 12359 3579 12357 |
| 4 29 359 | 1 25 7 | 6 359 8 |
|----------------------+----------------------+----------------------|
| 18 14678 1478 | 5 3 2 | 48 468 9 |
| 38 5 348 | 7 9 6 | 2348 1 23 |
| 2 69 39 | 48 1 48 | 7 356 35 |
*--------------------------------------------------------------------*
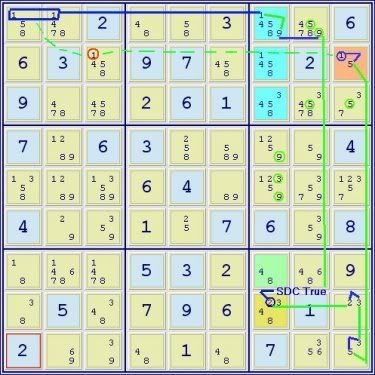
The core of the SDC in r123c7 is in blue, the A cell is in brown at r2c9, the B cell is in green at r7c7 and since this is an aaals core with 6 digit values in 3 squares, a C cell is necessary & is present in gold at r8c7 to complete the pattern. But for the 2 at r8c7 this would be a full SDC -the digits circled in green are the eliminations that would be possible from the full pattern:
(1=5)r2c9 - (5=3)r9c9 - (3=2)r8c9 - (2)r8c7 = SDC(134589)r123c7/(15)r2c9/(48)r7c7/(348)r8c7 - (9)r1c8 = (9-1)r1c7 = grp(1)r1c12
=> r2c3<>1 -> linebox(1)r2c79:r1c7<>1
NL: r2c3 -1- r2c9 -5- r9c9 -3- r8c9 -2- r8c7 =2= SDC(134589)r123c7/(15)r2c9/(48)r7c7/(348)r8c7 -9- r1c8 =9= r1c7 =1= r1c12 -1- r2c3 => r2c3<>1 -> linebox(1)r2c79:r1c7<>1

Red highlights the r8c7<>2 elimination which exposes the full SDC.
(2=3)r8c9 - (3=8)r8c1 - (8=1)r7c1 - r1c1 = (1-7)r1c2 = r1c8 - r5c8 = (7)r5c9 => r5c9<>2, r8c9=2, r8c7<>2
NL: r5c9 =7= r5c8 -7- r1c8 =7= r1c2 =1= r1c1 -1- r7c1 -8- r8c1 -3- r8c9 -2- r5c9 => r5c9<>2, r8c9=2, r8c7<>2
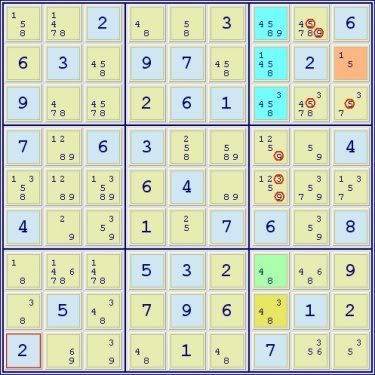
SDC(134589)r123c7/(15)r2c9/(48)r7c7/(348)r8c7 => r3c89<>5, r1c8<>59, r45c7<>9, r5c7<>3 -> r1c7=9
Final chains which complete the solution:
(3=7)r3c9 - r1c8 = (7-1)r1c2 = r1c1 - (1=8)r7c1 - (8=3)r8c1 - r8c7 = r3c7 - loop => r1c2<>48, r3c8<>37, r8c3<>3
NL: r1c8 =7= r1c2 =1= r1c1 -1- r7c1 -8- r8c2 -3- r8c7 =3= r3c7 -3- r3c9 -7- r1c8 => r1c2<>48, r3c8<>37, r8c3<>3
(4)r2c6 = xw(4)r28c37 - (4=8)r7c7 - (8=1)r7c1 - r1c1 = (1-7)r1c2 = r1c8 - (7=3)r3c9 - r3c7 = r8c7 - grp(3)r9c89 = (3-9)r9c3 = r9c2 - (9=2)r6c2 - (2=5)r6c5 - r1c5 = (5)r2c6 - loop
=>r45c2<>9, r4c5<>5, r7c238<>8 -> linebox(8)r78c7:r23c7<>8
NL: r2c6 =4= xw(4)r28c37 -4- r7c7 -8- r7c1 -1- r1c1 =1= r1c2 =7= r1c8 -7- r3c9 -3- r3c7 =3= r8c7 -3- r9c89 =3= r9c3 =9= r9c2 -9- r6c2 -2- r6c5 -5- r1c5 =5= r2c6 =>r45c2<>9, r4c5<>5, r7c238<>8 -> linebox(8)r78c7:r23c7<>8
(4)r3c2 = r7c2 - (4=8)r8c3 - grp(8)r78c1 = hp(58-1)r15c1 = (1-7)r1c2 = (7-8)r1c8 = (8)r3c8 => r3c3<>4=8
NL: r3c8 -4- r3c2 =4= r7c2 -4- r8c3 -8- r78c1 =8= hp(58)r15c1 -1- r1c1 =1= r1c2 =7= r1c8 =8= r3c8 => r3c3<>4=8
(2=5)r6c5 - (5=8)r1c5 - (8=4)r1c4 - r1c8 = grp(4)r23c7 - (4=8)r7c7 - (8=1)r7c1 - r7c3 = r5c3 - als(1=28)r45c2
=> r6c2<>2=9, r9c2=6, r7c8=6, r6c5=2 etc.
NL: r6c2 -2- r6c5 -5- r1c5 -8- r1c4 -4- r1c8 =4= r23c7 -4- r7c7 -8- r7c1 -1- r7c3 =1= r5c3 -1- als(28)r45c2 -2- r6c2 => r6c2<>2=9, r9c2=6, r7c8=6, r6c5=2 etc.
Singles to the End

