http://forum.enjoysudoku.com/viewtopic.php?t=6410
http://forum.enjoysudoku.com/viewtopic.php?t=6411
http://forum.enjoysudoku.com/viewtopic.php?t=6462
What I've Learned So Far:
Sometimes one can be excited by the apparent promise of a 'new' pattern only to find that in actual solving it is of limited or no use. For me, this has not turned out to be true of either Sue De Coq or, particularly, the Almost Sue De Coq. In solving the Extreme puzzles starting at the SSTS position, it is now my custom to search for both these patterns at the start of solving. This only takes a few minutes. Sometimes there are either no, or not useful, aSDC patterns, but more often than I even expected there are aSDC patterns that are useful at the moment, become useful later on or which (more rarely) convert to a full SDC.
Since I first posted on the Almost Sue De Coq concept, I have been particularly interested in seeing if during actual solving, chains I created using an aSDC pattern can be more easily replicated using the patterns that underly SDC, but for me at least that hasn't turned out to be the case. In fact, the experience has given rise to Don's #1 rule of pattern-solving: The usefulness of a pattern is inversely proportional to the difficulty with which it can be found.
Using the simplified rules for finding the SDC pattern, both the aSDC and the full SDC patterns are very easy to find. To recap for the SDC pattern:Look for a core consisting of a) 4 different digit values (aals) or 5 (aaals) in 2 cells in a row or column, all in the same box or b) 5 (aals) or 6 (aaals) different digit values in 3 cells in a row or column all in the same box. In the same box, look for a bivalue cell (let’s call it A) containing 2 digits that are also present in the core, then, in the same row or column (as the case may be) look for a bivalue cell (let’s call it B) containing 2 other digits from the core, but which are not the same digits as were in bivalue cell A. In addition to the above, if the Sue De Coq is the aaals-type (ie. 5 digit values in 2 cells or 6 in 3 cells) there must also be one more cell in the row or column or box (let’s call it C) that contains one more digit equal to a digit value in the core, but not present in the other 2 bivalue cells A and B. Usually, in addition to that digit, cell C can only contain digits that are already present in cell B (if cell C is in the row or column) or cell A (if cell C is in the box). This description covers the vast majority of typical aSDC or SDC that one will find in actual puzzles.
In this thread (ASI#2c) I present a full solution for Extreme #118 and in the one that follows (ASI#2d), a full solution for Extreme #122, both which I believe are particularly good examples of the power and efficiency of aSDC and SDC in typical pattern solving. (Obviously, these solutions are not presented as the only possible solutions.) Both AIC and NL notation is used. Nice Loops are only my '2nd language' so feel free to suggest changes in the NL notation used below.
(Abbreviations used: als=almost locked set, hp=hidden pair, grp=group, linebox=locked candidates at line/column->box intersections)
Extreme #118 ER=8.3 SSTS position:
- Code: Select all
*-----------------------------------------------------------------------------*
| 458 9 57 | 2 3457 1 | 58 6 348 |
| 12458 2457 3 | 457 45 6 | 9 1458 1248 |
| 12456 245 1256 | 8 3459 359 | 7 145 1234 |
|-------------------------+-------------------------+-------------------------|
| 2569 1 4 | 567 2568 257 | 68 3 79 |
| 7 23 26 | 469 234689 239 | 168 18 5 |
| 3569 8 56 | 567 1 357 | 4 2 79 |
|-------------------------+-------------------------+-------------------------|
| 1235 2357 8 | 5679 2569 4 | 125 157 16 |
| 245 2457 9 | 1 256 257 | 3 4578 468 |
| 1245 6 1257 | 3 257 8 | 125 9 14 |
*-----------------------------------------------------------------------------*
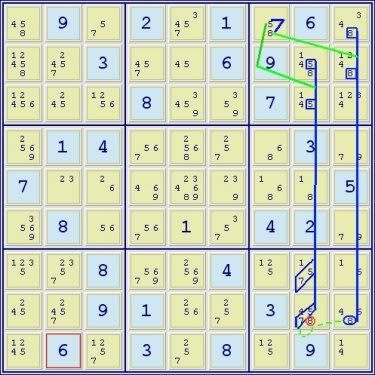
(8)r8c9 = grp(8)r12c9 - (8=5)r1c7 - grp(5)r23c8 = hp(57)r78c8 => r8c8<>8, r8c9=8, r7c9=6, r8c5=6
NL: r8c8 -8- r8c9 =8= r12c9 -8- r1c7 -5- r23c8 =5= hp(57)r78c8 -8- r8c8 => r8c8<>8, r8c9=8, r7c9=6, r8c5=6
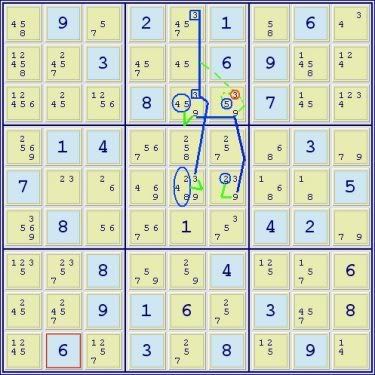
AUR(39)r35c56
||
(45-9)r3c5 = (9)r3c6
||
(248-3)r5c5 = grp(3)r13c5
||
(2-9)r5c6 = (9)r3c6
||
(5)r3c6
=> r3c6<>3 -> linebox(3)r56c6: r5c5<>3
(not sure how to express this in NL notation)
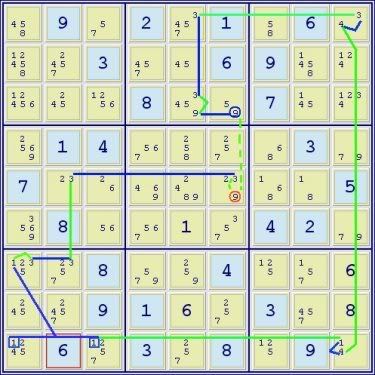
(9)r3c6 = (9-3)r3c5 = r1c5 - (3=4)r1c9 - (4=1)r9c9 - grp(1)r9c13 = (1-3)r7c1 = r7c2 - r5c2 = (3)r5c6
=> r5c6<>9, r3c6=9
NL: r5c6 -9- r3c6 =9= r3c5 =3= r1c5 -3- r1c9 -4-r9c9 -1- r9c13 =1= r7c1 =3= r8c2 -3- r5c2 =3= r5c6
=> r5c6<>9, r3c6=9
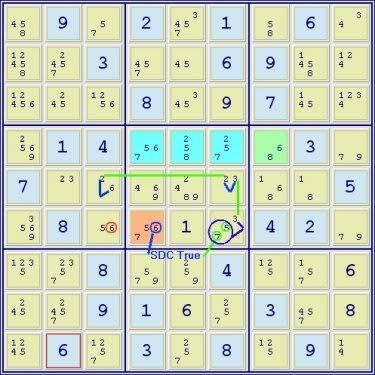
[Here the aSDC is used to bring down the puzzle. Edit: In view of the naked pair in the preceding graphic, the latter is no longer true, but the aSDC as an example is still useful nonetheless.] The core of the SDC is in blue, the A cell is brown and the B cell green. But for the 6 in r6c4 it would be a full SDC. Also, note that the strong link in r6c6 is made possible by the fact that if the SDC were true, digits 5 and 7 could be removed. It is interesting to me that, at least as far as I could tell, at the beginning (ie. SSTS position), the aSDC was of no value, but here it had become, due to other exclusions, very useful.
(6)r6c4 = SDC(25678)r4c456/(68)r4c7/(57)r6c4 - (57=3)r6c6 - (3=2)r5c6 - (2=6)r5c3
=> r6c3<>6=5 -> r1c3=7 -> r9c5 =7 -> r2c4=7
NL: r6c3 -6- r6c4 =6= SDC(25678)r4c456/(68)r4c7/(57)r6c4 -57- r6c6 -3- r5c6 -2- r5c6 -6- r6c3
=> r6c3<>6=5 -> r1c3=7 -> r9c5 =7 -> r2c4=7 etc.
(I have a feeling the portion of the NL directly following the SDC ie. -57- may not be the correct notation.)
Singles to the End
