The New Sudoku Players' Forum

[denis_berthier]

Code: Select all

  +-------+-------+-------+
  ! . . 6 ! . . 7 ! . . 9 !
  ! . 1 . ! . 9 . ! . 3 . !
  ! 9 . . ! 1 . . ! 5 . . !
  +-------+-------+-------+
  ! . . 4 ! . . 8 ! . . 5 !
  ! . 2 . ! . 4 . ! . 9 . !
  ! 6 . . ! 3 . . ! 1 . . !
  +-------+-------+-------+
  ! . . 1 ! . . 3 ! . . 6 !
  ! . 6 . ! . 5 . ! . 8 . !
  ! 4 . . ! 7 . . ! 2 . . !
  +-------+-------+-------+

..6..7..9.1..9..3.9..1..5....4..8..5.2..4..9.6..3..1....1..3..6.6..5..8.4..7..2..

[Mauriès Robert]

Hi Denis,
Not easy this puzzle.
I find the solution quite quickly with T&E(1), so I should solve it with "reasonable" length anti-tracks, but by hand it seems tedious, so I didn't insist.
With DFS of depth 2 I also manage to solve quite easily.
An interesting way that I didn't manage to exploit properly is the backdoor of size 2: 1r4c5+9r4c4, which corresponds to P'(19r4b4) : (-19r4b4) => solution.
Cordialy
Robert

[denis_berthier]

Hi Denis,
Not easy this puzzle.

SER = 9.3.
I intended it as a counterpoint to the puzzle here: http://forum.enjoysudoku.com/help-to-bring-an-se-9-3-to-around-se-7-5-t38397.html
But it happens to be 9.5 instead of the announced 9.3.
A 9.3 is never easy. But in the present case it's on the easy side of the 9.3s.

I find the solution quite quickly with T&E(1), so I should solve it with "reasonable" length anti-tracks, but by hand it seems tedious, so I didn't insist.

It can indeed be solved by whips[≤11], giving a typical resolution path of a 9.0 or 9.1:

Code: Select all

***********************************************************************************************
***  SudoRules 20.1.s based on CSP-Rules 2.1.s, config = W+SFin
***  Using CLIPS 6.32-r778
***********************************************************************************************
singles ==> r1c8 = 1, r9c8 = 5
182 candidates, 974 csp-links and 974 links. Density = 5.91%
t-whip[4]: r5n6{c6 c7} - r5c4{n6 n5} - c6n5{r6 r2} - r2n6{c6 .} ==> r4c4 ≠ 6
z-chain[5]: c5n1{r4 r9} - c5n6{r9 r3} - c8n6{r3 r4} - r4n2{c8 c4} - r6c5{n2 .} ==> r4c5 ≠ 7
hidden-single-in-a-block ==> r6c5 = 7
whip[9]: b3n2{r3c9 r2c9} - b1n2{r2c3 r1c1} - r7n2{c1 c4} - r4n2{c4 c8} - c8n6{r4 r3} - c8n7{r3 r7} - r7n4{c8 c7} - b3n4{r2c7 r3c9} - r3c6{n4 .} ==> r3c5 ≠ 2
whip[9]: r7n5{c1 c2} - r1n5{c2 c4} - r5c4{n5 n6} - r5c6{n6 n1} - r4c5{n1 n2} - r7c5{n2 n8} - c4n8{r7 r2} - c1n8{r2 r1} - r1n2{c1 .} ==> r5c1 ≠ 5
whip[10]: r7c8{n7 n4} - r7c7{n4 n9} - r8c7{n9 n3} - r9c9{n3 n1} - c5n1{r9 r4} - c6n1{r5 r8} - r8n4{c6 c4} - c4n9{r8 r4} - b5n2{r4c4 r6c6} - r6c8{n2 .} ==> r8c9 ≠ 7
whip[11]: r4c4{n2 n9} - r8c4{n9 n4} - r7c4{n4 n8} - r7c5{n8 n2} - r4n2{c5 c8} - c8n6{r4 r3} - c8n7{r3 r7} - r7n4{c8 c7} - r1n4{c7 c2} - r1n5{c2 c1} - r7c1{n5 .} ==> r1c4 ≠ 2
whip[9]: r1n2{c1 c5} - r1n3{c5 c2} - c2n4{r1 r3} - r3c6{n4 n6} - c8n6{r3 r4} - r4n2{c8 c4} - r4n9{c4 c2} - c2n7{r4 r7} - r7n5{c2 .} ==> r1c1 ≠ 5
t-whip[9]: r5c4{n6 n5} - c6n5{r6 r2} - r1n5{c4 c2} - c2n4{r1 r3} - c6n4{r3 r8} - r8n1{c6 c9} - r9c9{n1 n3} - c2n3{r9 r4} - c7n3{r4 .} ==> r5c7 ≠ 6
whip[1]: r5n6{c6 .} ==> r4c5 ≠ 6
t-whip[5]: r6n8{c3 c9} - r6n4{c9 c8} - r6n2{c8 c6} - r4c5{n2 n1} - c1n1{r4 .} ==> r5c1 ≠ 8
t-whip[4]: c1n8{r2 r7} - r7n5{c1 c2} - r1n5{c2 c4} - c4n8{r1 .} ==> r2c3 ≠ 8
whip[7]: c1n5{r7 r2} - c1n8{r2 r1} - r1n2{c1 c5} - r7n2{c5 c4} - r4n2{c4 c8} - r6c8{n2 n4} - r7c8{n4 .} ==> r7c1 ≠ 7
whip[7]: c1n8{r2 r7} - b8n8{r7c4 r9c5} - r9n6{c5 c6} - b8n1{r9c6 r8c6} - c6n9{r8 r6} - r6c2{n9 n5} - r7n5{c2 .} ==> r1c2 ≠ 8
whip[7]: c1n8{r2 r7} - b8n8{r7c4 r9c5} - r9n6{c5 c6} - b8n1{r9c6 r8c6} - c6n9{r8 r6} - r6c2{n9 n5} - r7n5{c2 .} ==> r3c2 ≠ 8
whip[7]: r1n2{c1 c5} - c6n2{r2 r6} - r6c8{n2 n4} - r6c9{n4 n8} - r5n8{c9 c3} - r3n8{c3 c5} - c5n3{r3 .} ==> r8c1 ≠ 2
naked-triplets-in-a-column: c1{r4 r5 r8}{n3 n1 n7} ==> r2c1 ≠ 7, r1c1 ≠ 3
z-chain[5]: b7n2{r8c3 r7c1} - r1c1{n2 n8} - r1c7{n8 n4} - c2n4{r1 r3} - b1n7{r3c2 .} ==> r8c3 ≠ 7
z-chain[6]: r8n7{c1 c7} - r4n7{c7 c8} - c8n6{r4 r3} - c5n6{r3 r9} - c5n1{r9 r4} - c1n1{r4 .} ==> r5c1 ≠ 7
whip[6]: c1n3{r5 r8} - r8n7{c1 c7} - r4c7{n7 n6} - b3n6{r2c7 r3c8} - c8n7{r3 r4} - c1n7{r4 .} ==> r4c2 ≠ 3
t-whip[6]: r1n5{c4 c2} - c2n4{r1 r3} - c2n3{r3 r9} - r9c9{n3 n1} - b8n1{r9c5 r8c6} - c6n4{r8 .} ==> r2c6 ≠ 5, r1c4 ≠ 4
whip[1]: c6n5{r6 .} ==> r5c4 ≠ 5
naked-single ==> r5c4 = 6
t-whip[7]: r1n2{c1 c5} - r1n3{c5 c2} - c2n4{r1 r3} - r3c6{n4 n6} - c8n6{r3 r4} - r4n2{c8 c4} - r7n2{c4 .} ==> r2c1 ≠ 2
whip[5]: r2c1{n8 n5} - c4n5{r2 r1} - c4n8{r1 r7} - r7c5{n8 n2} - r7c1{n2 .} ==> r2c7 ≠ 8
whip[5]: r2c1{n8 n5} - c4n5{r2 r1} - c4n8{r1 r7} - r7c5{n8 n2} - r7c1{n2 .} ==> r2c9 ≠ 8
t-whip[7]: r7n2{c5 c1} - r1n2{c1 c5} - r1n3{c5 c2} - c2n4{r1 r3} - r3c6{n4 n6} - c8n6{r3 r4} - r4n2{c8 .} ==> r8c4 ≠ 2
t-whip[4]: r9n9{c3 c6} - r9n6{c6 c5} - b8n1{r9c5 r8c6} - r8n2{c6 .} ==> r8c3 ≠ 9
whip[6]: c7n9{r8 r7} - c4n9{r7 r4} - r8c4{n9 n4} - b9n4{r8c7 r7c8} - r7n7{c8 c2} - r4c2{n7 .} ==> r8c6 ≠ 9
x-wing-in-columns: n9{c3 c6}{r6 r9} ==> r9c2 ≠ 9, r6c2 ≠ 9
t-whip[3]: c1n8{r2 r7} - r9c2{n8 n3} - b1n3{r1c2 .} ==> r3c3 ≠ 8
whip[1]: b1n8{r2c1 .} ==> r7c1 ≠ 8
z-chain[3]: r6c2{n5 n8} - c3n8{r5 r9} - c3n9{r9 .} ==> r6c3 ≠ 5
biv-chain[3]: r6c2{n5 n8} - r6c3{n8 n9} - b7n9{r9c3 r7c2} ==> r7c2 ≠ 5
singles ==> r7c1 = 5, r2c1 = 8, r1c1 = 2, r8c3 = 2
biv-chain[3]: c4n8{r7 r1} - r1n5{c4 c2} - r6c2{n5 n8} ==> r7c2 ≠ 8
whip[1]: r7n8{c5 .} ==> r9c5 ≠ 8
naked-pairs-in-a-column: c2{r4 r7}{n7 n9} ==> r3c2 ≠ 7
whip[1]: b1n7{r3c3 .} ==> r5c3 ≠ 7
whip[1]: r5n7{c9 .} ==> r4c7 ≠ 7, r4c8 ≠ 7
hidden-pairs-in-a-block: b8{r7c4 r7c5}{n2 n8} ==> r7c4 ≠ 9, r7c4 ≠ 4
whip[1]: r7n4{c8 .} ==> r8c7 ≠ 4, r8c9 ≠ 4
naked-pairs-in-a-block: b9{r8c9 r9c9}{n1 n3} ==> r8c7 ≠ 3
whip[1]: b9n3{r9c9 .} ==> r5c9 ≠ 3
biv-chain-rn[3]: r8n3{c1 c9} - r8n1{c9 c6} - r5n1{c6 c1} ==> r5c1 ≠ 3
stte

Allowing g-whips or braids doesn't make it simpler (doesn't change the rating).

[m_b_metcalf]

2r2c4, stte.

[denis_berthier]

2r2c4, stte.

Hi Mike,
Do you mean that n2r2c4 is a backdoor or is there more than that?

[m_b_metcalf]

2r2c4, stte.

Do you mean that n2r2c4 is a backdoor or is there more than that?

Denis, No, just that. Regards, Mike

[yzfwsf]

backdoor:
r2c4=2
r7c2=9
r9c6=9

[Mauriès Robert]

Hi all,
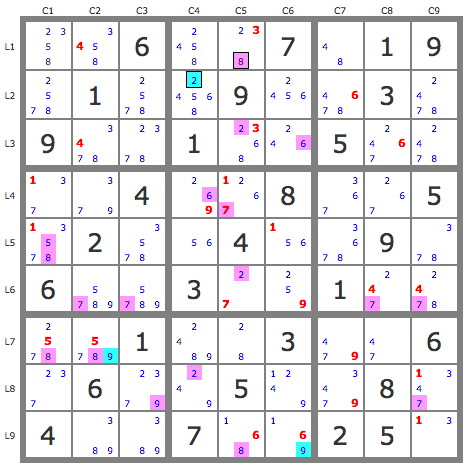
Mapping of backdoors (blue) and candidates to be eliminated (purple) with only singles. I get this cartography with a PHP program associated with my website that looks for P(A) tracks built with only singles and lead to contradiction.
Some of the targets of Denis' resolution can be found.
Obviously, this mapping evolves after each elimination.
Robert

[Cenoman]

Note: for better reading embedded AIC's in multi krakens, their connecting strong link is tagged *=*
20 steps:

Code: Select all

 +------------------------+------------------------+-----------------------+
 |  235-8   345-8  6      |  2458    238    7      |  48     1      9      |
 |  58-27   1      2578   |  24568   9      2456   |  4678   3      2478   |
 |  9       347-8  2378   |  1       2368   246    |  5      2467   2478   |
 +------------------------+------------------------+-----------------------+
 |  137     379    4      |  29-6    1267   8      |  367    267    5      |
 |  137-58  2      3578   |  56      4      156    |  3678   9      378    |
 |  6       5789   5789   |  3       7-2    259    |  1      247    2478   |
 +------------------------+------------------------+-----------------------+
 |  58-27   5789   1      |  2489    28     3      |  479    47     6      |
 |  237     6      2379   |  249     5      149-2  |  3479   8      1347   |
 |  4       389    389    |  7       168    169    |  2      5      13     |
 +------------------------+------------------------+-----------------------+

1. (2)r4c45 = (2-6)r4c8 = r3c8 - r2c7 = r2c46 - (6=382)r137c5 => -2 r6c5; 1 placement

2. (6)r4c8 = r3c8 - r3c5 = (6-12)r49c5 = (29)b5p19 => -6 r4c4

3. Kraken AALS (3589)r69c2
(5)r6c2-r7c2=(5-2)r7c1=(2)r7c45
(89)r69c2 - r4c2 = r4c4 - (9=482)b8p124
(3)r9c2 - (3=1)r9c9 - r8c9 = (1)r8c6
=> -2 r8c6

4. (2)r1c1 = r1c45 - r23c6 = r4c8 - [(6)r4c8 = r3c8 - (6*=*2)r3c6] = (4)r3c6 - r3c2 = r1c2 - (4=8)r1c7 => -8 r1c1

5. Kraken column (8)r257c1
(8)r2c1
(8)r5c1 - r6c23 = (2)r4c8 - [(6)r4c8 = r3c8 - (6*=*2)r3c6] = (4)r3c6 - r3c2 = (4)r1c2
(8)r7c1 - [(5)r7c1 = r7c2 - (5*=*9)r6c2 - r4c2 = r4c4 - (9=428)b8p124] = (8)r6c2
=> -8 r1c2

6. Kraken column (8)r257c1
(8)r2c1
(8)r5c1 - [(1)r5c1 = r5c6 - (1*=*2)r4c5 - (2=958)r6c236] = (6)r4c5 - r5c4 = (6-8)r2c4 = [(8)r3c5*=*r1c45 - (8=4)r1c7 - r1c2 = (4)r3c2]
(8)r7c1 - [(5)r7c1 = r7c2 - (5*=*9)r6c2 - r4c2 = r4c4 - (9=428)b8p124] = (8)r6c2
=> -8 r3c2

7. Kraken column (8)r257c1
(8)r2c1 - r2c4 = [(5)r56c3 = r2c3 - r1c12 = (5-8)r1c4*=*r7c4 - (8=2)r7c5 - (2=165)b5p246]
(8)r5c1
(8)r7c1 - (8=2)r7c5 - (2=165)b5p246
=> -5 r5c1

8. Kraken cell (3479)r8c7
(3)r8c7 - (3=1)r9c9 - r9c5 = r4c5 - r5c6 = (1)r5c1
(4)r8c7 - [(4=8)r1c7 - r1c4*=*(8-4)r7c4 = (4)r7c78] = (8-6)r2c4 = r5c4 - r4c5 = [(1)r5c1 = r5c6 - (1*=*2)r4c5 - (2=958)r6c236]
(7)r8c7 - (7=4)r7c8 - r6c8 = (4-8)r6c9 = (8)r6c23
(9)r8c7 - r8c6 = [(1)r5c1 = r5c6 - r4c5 = (1-69)r9c56*=*r6c6 - (9=58)r6c23]
=> -8 r5c1

9. (8)r2c1 = r23c3 - r5c3 = (8-592)r6c236 = r23c6 - r1c45 = (2)r1c1^ - (2=137)r458c1 => -2^7 r2c1

10. (7=4)r7c8 - (4=2)r6c8 - r6c6 = r23c6 - r1c45 = r1c1 - (2=137)r458c1 => -7 r7c1

11. Kraken row (8)r3c359
(8)r3c3 - r2c1 = (8)r7c1
(8)r3c5 - (8=2)r7c5
(8)r3c9 - (8=42)r6c89 - r6c6 = r23c6 - r1c45 = (2)r1c1
=> -2 r7c1

12. Kraken row (8)r3c359
(8)r3c3 - r5c3 = (8-592)r6c236 = r23c6 - r1c45 = (2)r1c1
(8-3)r3c5 = (3)r1c5
(8)r3c9 - (8=42)r6c89 - r6c6 = r23c6 - r1c45 = (2)r1c1
=> -3 r1c1; 2 placements & basics

Code: Select all

 +----------------------+------------------------+-----------------------+
 |  2     345    6      |  458     38     7      |  48     1      9      |
 |  58    1      578    |  24568   9      2456   |  4678   3      2478   |
 |  9     347    378    |  1       2368   246    |  5      2467   2478   |
 +----------------------+------------------------+-----------------------+
 |  137   379    4      |  29      16-2   8      |  367    267    5      |
 |  137   2      3578   |  6-5     4      156    |  3678   9      378    |
 |  6     589    589    |  3       7      259    |  1      24     248    |
 +----------------------+------------------------+-----------------------+
 |  58    5789   1      |  2489    28     3      |  479    47     6      |
 |  37    6      2      |  49      5      149    |  3479   8      1347   |
 |  4     389    389    |  7       168    169    |  2      5      13     |
 +----------------------+------------------------+-----------------------+

13. (5=8)r1c4 - (8=36)r13c5 - r2c4 = (6)r5c4 => -5 r5c4; 1 placement

14. Kraken row (7)r4c1278
(7-1)r4c1 = (1)r4c5
(7r4c27) - (r7c2,r8c7) = (7-3)r8c1 = r8c79 - (3=1)r9c9 - r9c5 = (1)r4c5
(7-6)r4c8 = r3c8 - (6=382)r137c5
-----------------
=> -2 r4c5; 4 placements & basics

Code: Select all

 +--------------------+----------------------+-----------------------+
 |  2    345    6     |  458    38     7     |  48     1      9      |
 |  58   1      57-8  |  2458   9      246   |  4678   3      2478   |
 |  9    347    37-8  |  1      2368   246   |  5      2467   2478   |
 +--------------------+----------------------+-----------------------+
 |  37   79-3   4     |  29     1      8     |  367    267    5      |
 |  1    2      378   |  6      4      5     |  378    9      378    |
 |  6    58-9   589   |  3      7      29    |  1      24     248    |
 +--------------------+----------------------+-----------------------+
 |  58   5789   1     |  2489   28     3     |  479    47     6      |
 |  37   6      2     |  49     5      14-9  |  3479   8      1347   |
 |  4    389    39-8  |  7      68     169   |  2      5      13     |
 +--------------------+----------------------+-----------------------+

15. (9)r4c2 = r4c4 - (9=24)r6c68 - (4=7)r7c8 - r7c2 = r8c1 - (7=3)r4c1 => -3 r4c2

16. (9)r9c3 = r6c3 - (9=378)b4p126 => -8 r9c3

17. (1)r8c6 = r8c9 - (1=3)r9c9 - r9c23 = (3-7)r8c1 = r7c2 - (7=4)r7c8 - (4=29)r6c68 => -9 r8c6

18. Kraken cell (389)r9c2
(3)r9c2 - r13c2 = (3)r3c3
(8)r9c2 - r6c2 = (8)r56c3
(9)r9c2 - (9=378)b4p126
=> -8 r3c3

19. [(8)r2c1 = r7c1 - r7c4 = r2c4] = (8-5)r1c4 = r1c2 - (5=8)r2c1 => -8 r2c3; 2 placements & basics

20. (9)r4c2 = r4c4 - r6c6 = r9c6 - r9c23 = r7c2 => -9 r6c2; lclste

[Mauriès Robert]

Hi Cenoman,
Very nice resolution. You are "THE" Krakens specialist !
Robert