The New Sudoku Players' Forum

[surbier]

Hi,
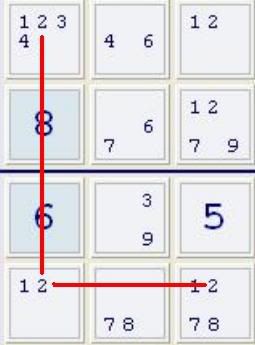
I could solve this SE=8.4 rated

Code: Select all

000050002070000090400800000100600800906000305002004007000003006090010070500020000


using ariadne's thread like long forcing chains, starting on the bi-value cells.

Using more analytical methods, I get stuck at this point:

Code: Select all

 *--------------------------------------------------------------------*
 | 368    1368   1389   | 1347   5      179    | 1467   13468  2      |
 | 2368   7      135    | 1234   46     12     | 1456   9      138    |
 | 4      1236   159    | 8      67     1279   | 1567   35     13     |
 |----------------------+----------------------+----------------------|
 | 1      34     7      | 6      39     5      | 8      2      49     |
 | 9      48     6      | 12     78     1278   | 3      14     5      |
 | 38     5      2      | 19     38     4      | 169    16     7      |
 |----------------------+----------------------+----------------------|
 | 7      128    148    | 459    489    3      | 1245   1458   6      |
 | 2368   9      348    | 45     1      68     | 245    7      348    |
 | 5      1368   1348   | 47     2      678    | 149    1348   13489  |
 *--------------------------------------------------------------------*


I know there are some short forcing chains, but I'm more interested in other methods to solve this one.

[eleven]

I only see an elimination from the diagonal UR 12 here:

Code: Select all

 *--------------------------------------------------------------------*
 | 368    1368   1389   | 1347   5      179    | 1467   13468  2      |
 | 2368   7      135    |#1234   46    #12     | 1456   9      138    |
 | 4      1236   159    | 8      67     1279   | 1567   35     13     |
 |----------------------+----------------------+----------------------|
 | 1      34     7      | 6      39     5      | 8      2      49     |
 | 9      48     6      |#12     78    #1278   | 3      14     5      |
 | 38     5      2      | 19     38     4      | 169    16     7      |
 |----------------------+----------------------+----------------------|
 | 7      128    148    | 459    489    3      | 1245   1458   6      |
 | 2368   9      348    | 45     1      68     | 245    7      348    |
 | 5      1368   1348   | 47     2      678    | 149    1348   13489  |
 *--------------------------------------------------------------------*

With the strong links for 2 in r5 and c3 you can eliminate 1 from r2c4 and r5c6.
[Edit: Sorry, it should say: With the strong links for 2 in r5 and c4 you can eliminate 2 from r2c4 and r5c6.]
No great help after all, but its a bit easier now.

[Luke]

Aren't the eliminations on 2 instead of 1?

According to Havard:

With a Unique Rectangle with the numbers [ab] that has two cells with "extra candidates" ([xabx]), and these cells are on a diagonal from each other, and you have a strong link between any two of the cells in the Rectangle for candidate [a], then you can eliminate candidate [a] from the cell with extra candidates that is not part of the strong link.

The 2 in r2c4 (an extra candidate cell) is not part of the strong link in row 5.
The 2 in r5c6 (another extra candidate cell) is not part of the strong link in column 4.
This means both r2c4 and r5c6 <> 2, ==> r5c4 = 2. (Link to quoted post is here.)

I just remember this: if there's diagonal bivalues, the strong candidate must be in the "elbow."

[daj95376]

I only see an elimination from the diagonal UR 12 here:

Code: Select all

 *--------------------------------------------------------------------*
 | 368    1368   1389   | 1347   5      179    | 1467   13468  2      |
 | 2368   7      135    |#1234   46    #12     | 1456   9      138    |
 | 4      1236   159    | 8      67     1279   | 1567   35     13     |
 |----------------------+----------------------+----------------------|
 | 1      34     7      | 6      39     5      | 8      2      49     |
 | 9      48     6      |#12     78    #1278   | 3      14     5      |
 | 38     5      2      | 19     38     4      | 169    16     7      |
 |----------------------+----------------------+----------------------|
 | 7      128    148    | 459    489    3      | 1245   1458   6      |
 | 2368   9      348    | 45     1      68     | 245    7      348    |
 | 5      1368   1348   | 47     2      678    | 149    1348   13489  |
 *--------------------------------------------------------------------*

With the strong links for 2 in r5 and c3 you can eliminate 1 from r2c4 and r5c6.
No great help after all, but its a bit easier now.

Do you have a typo? I get an alternate elimination -- [r5c4]<>1.

[Luke]

With the strong links for 2 in r5 and c3 you can eliminate 1 from r2c4 and r5c6.

Do you have a typo? I get an alternate elimination -- [r5c4]<>1.

Also c3 sh/be c4

[Glyn]

As far as I can see that UR only leads to r2c4<>1 and r5c4=2.
Now if only we could have proved r1c4<>1 then we could really have cleaned up with it. Leaving only singles and an xy-wing to finish.

[Luke]

Code: Select all

*--------------------------------------------------------------------*
 | 368    1368   1389   | 1347   5      179    | 1467   13468  2      |
 | 2368   7      135    |#1234   46    #12     | 1456   9      138    |
 | 4      1236   159    | 8      67     1279   | 1567   35     13     |
 |----------------------+----------------------+----------------------|
 | 1      34     7      | 6      39     5      | 8      2      49     |
 | 9      48     6      |#12     78    #1278   | 3      14     5      |
 | 38     5      2      | 19     38     4      | 169    16     7      |
 |----------------------+----------------------+----------------------|
 | 7      128    148    | 459    489    3      | 1245   1458   6      |
 | 2368   9      348    | 45     1      68     | 245    7      348    |
 | 5      1368   1348   | 47     2      678    | 149    1348   13489  |
 *--------------------------------------------------------------------*

As far as I can see that UR only leads to r2c4<>1 and r5c4=2.

Since we agree r5c4=2, I shouldn't quibble. However, how does this UR prove r2c4<>1 (one of eleven's initial assertions)? In order for this to be true, placing 1 in r2c4 would have to force 1 into r5c6, which if I'm not mistaken, it does not.

Code: Select all

1  2
2  78

Then again, I'm often mistaken...

[eleven]

I am very sorry for these annoying typos, which brought some confusions. I was late and had no time to recheck, what i wrote.

As Glyn noted, also the 1 from r2c4 can be eliminated because of r2c4 -> r45c4<>1 (or r123c6<>1) -> r5c6=1, such leading to the deadly pattern also. I did not see that yesterday.

[Glyn]

My approach on this was the avoidance of the UR leads for example to one of these three conditions (just one of many ways):-
(a)r16c4=1
(b)r13c6=1
(c)r3c6=2
All lead to common results r5c4=2 and r2c4<>1.

If we had known that r1c4<>1 then condition (a) would have given us the extra reductions at r5c6 that crack the grid with the xy-wing. Sadly although true, proving that is probably as hard as the puzzle itself.

[Luke]

Ok, I got it now. If 1 is in r2c4, the only 1 left in box 5 is r5c6 and there's the DP.

[surbier]

I spotted the two pairs of [12] before posting this, but I didn't knew all the flavours of UR.
Thanks

[surbier]

... that crack the grid with the xy-wing....

Mmh, I don't see the xy-wing.

Code: Select all

 *--------------------------------------------------------------------*
 | 368    1368   1389   | 1347   5      179    | 1467   13468  2      |
 | 2368   7      135    | 34     46     12     | 1456   9      138    |
 | 4      1236   159    | 8      67     1279   | 1567   35     13     |
 |----------------------+----------------------+----------------------|
 | 1      34     7      | 6      39     5      | 8      2      49     |
 | 9      48     6      | 2      78     178    | 3      14     5      |
 | 38     5      2      | 19     38     4      | 169    16     7      |
 |----------------------+----------------------+----------------------|
 | 7      128    148    | 459    489    3      | 1245   1458   6      |
 | 2368   9      348    | 45     1      68     | 245    7      348    |
 | 5      1368   1348   | 47     2      678    | 149    1348   13489  |
 *--------------------------------------------------------------------*


There is (admittedly most of them found by scanraid)
- simple coloring in candidate 1 to eliminate 1 in r1c8
- aligned pair exclusion in block3 eliminating 3 in r2c9
- AIC mostly in row 5 and col 6 to delete 3 in r3c2
- this enables a line block interaction to cancel the 3 in r1c8
- with a rather more extended AIC one can delete the 8 in r8c1
- a further AIC even longer to cancel a 3 in r9c2
- finally an AIC with a groups to take off 3 in r2c3
- and pattern overlay deletes the 1 in r1c7

Code: Select all

 *--------------------------------------------------------------------*
 | 368    1368   1389   | 1347   5      179    | 467    468    2      |
 | 2368   7      15     | 34     46     12     | 1456   9      18     |
 | 4      126    159    | 8      67     1279   | 1567   35     13     |
 |----------------------+----------------------+----------------------|
 | 1      34     7      | 6      39     5      | 8      2      49     |
 | 9      48     6      | 2      78     178    | 3      14     5      |
 | 38     5      2      | 19     38     4      | 169    16     7      |
 |----------------------+----------------------+----------------------|
 | 7      128    148    | 459    489    3      | 1245   1458   6      |
 | 236    9      348    | 45     1      68     | 245    7      348    |
 | 5      168    1348   | 47     2      678    | 149    1348   13489  |
 *--------------------------------------------------------------------*


At this point I get stuck again. I didn't expect it such difficult.

[hobiwan]

At this point I get stuck again. I didn't expect it such difficult.

My solver still needs about 10 chains to solve it.

A bit shorter, but with one large Forcin Chain:

Grouped Discontinuous Nice Loop r3c2 -1- r1c23 =1= r1c46 -1- r2c6 -2- r2c1 =2= r3c2 => r3c2<>1
Forcing Chain Verity => r3c2<>6
r1c1=6 r3c2<>6
r1c2=6 r3c2<>6
r1c7=6 r3c7=7 r3c5=6 r3c2<>6
r1c8=6 r6c8=1 r1c4=1 r2c6=2 r3c2=2 r3c2<>6
Medium Steps (plus one XY-Chain)

[DonM]

At this point I get stuck again. I didn't expect it such difficult.

Although, the ER is not an exact measure of difficulty, it is accurate enough that when I see an ER=8.4 puzzle, I assume that it is not going to be any kind of a manual-solving pushover of a puzzle. That happens to be around the average difficulty level of puzzles we're solving on the other forum and it seems typical of the 8.4 level of puzzle that if you're solving it without nets, it just won't lie down and die.

[aran]

... that crack the grid with the xy-wing....

Mmh, I don't see the xy-wing.

Code: Select all

 *--------------------------------------------------------------------*
 | 368    1368   1389   | 1347   5      179    | 1467   13468  2      |
 | 2368   7      135    | 34     46     12     | 1456   9      138    |
 | 4      1236   159    | 8      67     1279   | 1567   35     13     |
 |----------------------+----------------------+----------------------|
 | 1      34     7      | 6      39     5      | 8      2      49     |
 | 9      48     6      | 2      78     178    | 3      14     5      |
 | 38     5      2      | 19     38     4      | 169    16     7      |
 |----------------------+----------------------+----------------------|
 | 7      128    148    | 459    489    3      | 1245   1458   6      |
 | 2368   9      348    | 45     1      68     | 245    7      348    |
 | 5      1368   1348   | 47     2      678    | 149    1348   13489  |
 *--------------------------------------------------------------------*


There is (admittedly most of them found by scanraid)
- simple coloring in candidate 1 to eliminate 1 in r1c8
- aligned pair exclusion in block3 eliminating 3 in r2c9
- AIC mostly in row 5 and col 6 to delete 3 in r3c2
- this enables a line block interaction to cancel the 3 in r1c8
- with a rather more extended AIC one can delete the 8 in r8c1
- a further AIC even longer to cancel a 3 in r9c2
- finally an AIC with a groups to take off 3 in r2c3
- and pattern overlay deletes the 1 in r1c7

Code: Select all

 *--------------------------------------------------------------------*
 | 368    1368   1389   | 1347   5      179    | 467    468    2      |
 | 2368   7      15     | 34     46     12     | 1456   9      18     |
 | 4      126    159    | 8      67     1279   | 1567   35     13     |
 |----------------------+----------------------+----------------------|
 | 1      34     7      | 6      39     5      | 8      2      49     |
 | 9      48     6      | 2      78     178    | 3      14     5      |
 | 38     5      2      | 19     38     4      | 169    16     7      |
 |----------------------+----------------------+----------------------|
 | 7      128    148    | 459    489    3      | 1245   1458   6      |
 | 236    9      348    | 45     1      68     | 245    7      348    |
 | 5      168    1348   | 47     2      678    | 149    1348   13489  |
 *--------------------------------------------------------------------*


At this point I get stuck again. I didn't expect it such difficult.

A non-forcing but longer alternative to Hobiwan's solution :

146r156c8=8r1c8-(8=1)r2c9-(1=3)r3c9-(3=5)r3c8-(5=14.#8r1c8)r7c8=>pair14r57c8 : => <14>r9c8
9r9c9=9r9c7-(9=16)r6c7=>pair16row6box6-1r6c4=1r5c6-(1=2)r2c6-2r2c1=2r8c1-(2=45)r8c7=>pair45r8c47-4r8c9=>pair38box9-(38)r9c9 : => <38>r9c9
49r9c79=1r9c79-1r7c8=1r56c8-1r6c7=1r6c4-1r5c6=(1-4)r5c8=4r4c9 : => <4>r8c9 and <1>r6c8 : =>r6c8=6 : <6> r6c7 r1c8
8 :r9c8=r8c9-r2c9=r2c1-r6c1=r5c2 : => <8> r9c2
A :6r9c2=6r9c6-(6=8)r8c6-(8=3)r8c9-(3=1)r3c9 : <1>r3c2
B :6r9c2=(6-2)r8c1=2r1c2 : <2>r3c2
=><6>r1c2
6r9c2=6r3c2-(6=7)r3c5-(7=8)r5c5-(8=4)r5c2-(4=3)r4c2-(3=1.#6r3c2)r2 :=> <1>r9c2 =>r9c2=6 : <6>r8c1 r3c2 r9c6 and r8c6=6
2r3c2=2r1c2-(2=3)r8c1-(3=8)r8c9-(8=1)r2c9-(1=2)r2c6-2r3c6=2r3c2 :=>r3c2=2. Eliminations and placements of 2.
Thereafter straightforward though not yet all singles.