The New Sudoku Players' Forum

[Mauriès Robert]

Hello,
I offer you this puzzle to know the best possible solution.

..........279.4.....6.5.79..9.8..6..4...7...3..5..1.2..54.6.8.....1.825..........

puzzle: Show

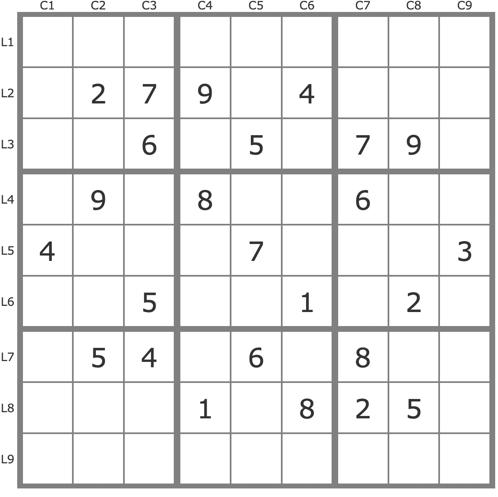
my resolution: Show

After simplification by basic techniques:

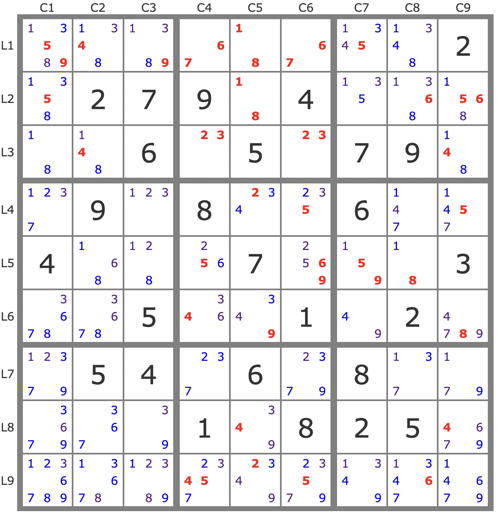
Then, successive eliminations with anti-tracks of length 9 maximum (without using the UR 23r27c46)
(-5r9c6)=>5r9c4->4r6c4->9r6c7->9r5c6->... => -9r9c6, -5r5c6
(-9r5c6)=>9r7c6->9r5c7->5r5c4->5r9c6->7r1c6->6r5c6->... -2r5c6
(-2r5c3)=>2r5c4->5r5c7->9r5c6->6r1c6->7r1c4->3r7c4->... r3c4 vide => r5c3=2
(-4r9c4)=>4r6c4->9r6c7->9r5c6->6r1c6->7r1c4->23r37c4->... => -237r9c4
(-3r8c3)=>9r8c3->9r1c1->5r1c7->5r5c4->4r9c4->3r8c5->... -3r8c12
(-4r3c2)=>4r3c9->4r8c5->(3r8c3 & 5r9c4->6r5c4->9r5c6->3r6c5)->3r4c1->3r1c2->... => -4r1c2 => r3c2=4
(-45r1c7)=>4r1c8->5r1c1->9r1c3->3r8c3->1r4c3->7r4c8->3r4c1->3r1c2->... => -3r1c7
(-5r1c7,-1r5c7)=>5r1c1->9r1c3->3r8c3->1r4c3->1r5c8->8r6c9->1r3c9->... => -1r1c7
(-4r6c4)=>4r9c4->4r8c9->... => -4r6c9
(-4r1c7)=>4r1c8->5r1c7->5r4c9->4r6c7->... => -4r9c7
(-9r6c7,-9r7c9)=>4r6c7->4r4c5->2r9c5->2r7c1->9r7c6->9r6c5->... => -9r6c9 => -9r9c7
(-7r7c89)=>13p17B9->9r7c9->9r5c6->6r1c6->7r1c4->... => -7r7c4 => r1c4=7 + 9 placements
(-4r4c8)=>7r4c8->3r4c1->3r1c2->1r9c2->3r9c7->3r2c8->6r9c8->... => -4r9c8 => r4c8=4 et -7r789c9, -7p19B7
(-3r2c1)=>3r1c2->1r9c2->3r9c7->... => -3r2c7 => r9c7=3
(-7r4c1)=>7r4c9->5r2c9->6r2c8->3r1c8->3r2c1->... => -3r4c1, end

Robert

[eleven]

Many ways to sove that, here are ny 2 cents.

Hidden Text: Show

Code: Select all

+----------------------------+----------------------------+----------------------------+
| 13589    1348     1389     | 67       18       67       | 1345     1348     2        |
| 1358     2        7        | 9        18       4        | 135      1368     1568     |
| 18       148      6        | 23       5       a23       | 7        9        148      |
+----------------------------+----------------------------+----------------------------+
| 137      9        123      | 8        234     a235      | 6        147     b1457     |
| 4        168      128      | 256      7       c2569     |b159      18       3        |
| 3678     3678     5        | 346      349      1        | 49       2        4789     |
+----------------------------+----------------------------+----------------------------+
| 12379    5        4        | 237      6        2379     | 8        137      179      |
| 3679     367      39       | 1        349      8        | 2        5        4679     |
| 1236789  13678    1389     | 23457    2349     23579    | 1349     13467    14679    |
+----------------------------+----------------------------+----------------------------+

(2=35)r36c6 - r4c9 = (5-9)r5c7 = 9r5c6 => -2r5c6

Hidden Text: Show

Code: Select all

*--------------------------------------------------------------------------------*
 |  13589     1348    1389    | b67      18     67      |  1345   1348    2       |
 |  1358      2       7       |  9       18     4       |  135    1368    1568    |
 |  18        148     6       | b23      5      23      |  7      9       148     |
 |----------------------------+-------------------------+-------------------------|
 |  1237      9       123     |  8      d234    235     |  6      147     1457    |
 |  4         168     128     | a56-2    7      569     |  159    18      3       |
 |  3678      3678    5       | c346    c349    1       | c49     2       4789    |
 |----------------------------+-------------------------+-------------------------|
 |  12379     5       4       | b237     6      2379    |  8      137     179     |
 |  3679      367     39      |  1       349    8       |  2      5       4679    |
 |  1236789   13678   12389   |  23457   2349   23579   |  1349   13467   14679   |
 *--------------------------------------------------------------------------------*

(56=2)r5c4 - (2=376)r371c4 - (3|6)r6c4 = 493r6c574 - (3|4=2)r4c6 => -2r5c4

This is a complex move, but to be honest, i like it

Code: Select all

+--------------------------+------------------------------+------------------------------+
| 13589    1348     1389   |   67       18       67       |   1345     1348     2        |
| 1358     2        7      |   9        18       4        |   135      1368     1568     |
| 18       148      6      |  e23       5       e23       |   7        9        148      |
+--------------------------+------------------------------+------------------------------+
| 137      9        13     |   8       d234     e235      |   6        147      1457     |
| 4        168      2      |   56       7     eca569      |  b15-9     18       3        |
| 3678     3678     5      | ec346     d349      1        | fb49       2        4789     |
+--------------------------+------------------------------+------------------------------+
| 12379    5        4      |  d237      6       d2379     |   8       e137     e179      |
| 3679     367      39     |   1        349      8        |   2        5        4679     |
| 1236789  13678    1389   |   23457    2349     23579    |  f1349     13467    14679    |
+--------------------------+------------------------------+------------------------------+

9r5c6 = 94r56c7 - r6c4,r5c6 = (94-2|3)r64c5 = 23r36c4 & r34c6 - (2|3=79)r7c46 - (7|9=13)r7c89 - (1|3=49)r96c7 => -9r5c7
then 2 singles, pair 23, UR23 => 7r7c6

Hidden Text: Show

Code: Select all

+--------------------------+---------------------------+------------------------------+
| 13589    1348     1389   |   7        18       6     |  e1345     1348     2        |
| 1358     2        7      |   9        18       4     |   135      1368     1568     |
| 18       148      6      |   23       5        23    |   7        9        148      |
+--------------------------+---------------------------+------------------------------+
| 137      9        13     |   8        234      235   |   6        147      1457     |
| 4        168      2      |  b56       7        9     |  a15       18       3        |
| 3678     3678     5      |   46       34       1     |   49       2        4789     |
+--------------------------+---------------------------+------------------------------+
| 1239     5        4      |   23       6        7     |   8        13       19       |
| 3679     367      39     |   1        349      8     |   2        5        4679     |
| 1236789  13678    1389   |  c45       2349     235   |  d1349     13467    14679    |
+--------------------------+---------------------------+------------------------------+

5r5c7 = r5c4 - (5=4)r9c4 - r9c7 = 4r1c7 => -5r1c7

Code: Select all

+----------------------+----------------------+----------------------+
|  5      1348   9     | 7      18     6      | 134    1348   2      |
|  138    2      7     | 9      18     4      | 135    1368   1568   |
|  18     148    6     | 23     5      23     | 7      9      148    |
+----------------------+----------------------+----------------------+
|  37     9      1     | 8      234    235    | 6      47     457    |
|  4     a68     2     | 56     7      9      | 15     18     3      |
|  3678  a3678   5     | 46    b34     1      | 49     2      4789   |
+----------------------+----------------------+----------------------+
|  129    5      4     | 23     6      7      | 8      13     19     |
| c679  ca67     3     | 1     b49     8      | 2      5      4679   |
|  12679  1-67   8     | 45     2349   235    | 1349   13467  14679  |
+----------------------+----------------------+----------------------+

(67=83)r856c2 - (3=49)r68c5 - (9=67)r8c12 => -67r9c2

Hidden Text: Show

Code: Select all

+-------------------+-----------------+--------------------+
| 5     348   9     | 7     18    6   | 134   134-8  2     |
| 138   2     7     | 9     18    4   | 135   136-8  1568  |
| 18   B48    6     | 23    5     23  | 7     9    Aa148   |
+-------------------+-----------------+--------------------+
| 37    9     1     | 8     234   235 | 6     47     457   |
| 4    C68    2     | 56    7     9   | 15  Dd18     3     |
| 3678  3678  5     | 46    34    1   | 49    2      479-8 |
+-------------------+-----------------+--------------------+
| 29    5     4     | 23    6     7   | 8    c13    b19    |
| 679   67    3     | 1     49    8   | 2     5      4679  |
| 2679  1     8     | 45    2349  235 | 349   3467   4679  |
+-------------------+-----------------+--------------------+

Kraken 148r3c9:
1r3c9 - r7c9 = r7c8 - (1=8)r5c8
4r3c9 - (4=8)r3c2 -r5c2 = r5c8
8r3c9
=> -8r6c9, r12c8

Hidden Text: Show

Code: Select all

+----------------+----------------+----------------+
| 5    38   9    | 7    18   6    |*34   134  2    |
| 138  2    7    | 9    18   4    | 5    136  168  |
| 18   4    6    | 23   5    23   | 7    9    18   |
+----------------+----------------+----------------+
| 37   9    1    | 8    234  23   | 6    47   5    |
| 4    6    2    | 5    7    9    | 1    8    3    |
| 378  38   5    | 6   *34   1    | 9-4  2    79   |
+----------------+----------------+----------------+
| 29   5    4    | 23   6    7    | 8    13   19   |
| 6    7    3    | 1    9    8    | 2    5    4    |
| 29   1    8    | 4   #23   5    |#39   67   67   |
+----------------+----------------+----------------+

w-wing 34 => -4r6c7

[DEFISE]

With chains of length <= 9 my FewSteps program found this:

Box/Line: 6r2b3 => -6r1c8 -6r1c9
Naked pairs: 23r3c46 => -3r3c1 -3r3c2 -2r3c9
Single(s): 2r1c9
Box/Line: 3r3b2 => -3r1c4 -3r1c5 -3r1c6 -3r2c5
whip[8]: r6c7{n9 n4}- c4n4{r6 r9}- r9n5{c4 c6}- c6n9{r9 r7}- b8n7{r7c6 r7c4}- r7c9{n7 n1}- r7c8{n1 n3}- r9c7{n3 .} => -9r5c7
Single(s): 9r5c6, 6r1c6, 7r1c4
Naked pairs: 23c4r37 => -2r5c4 -3r6c4 -2r9c4 -3r9c4
Single(s): 2r5c3
whip[8]: r5n5{c7 c4}- r9c4{n5 n4}- c7n4{r9 r6}- r4n4{c8 c5}- c5n2{r4 r9}- r7n2{c4 c1}- r7n9{c1 c9}- r6n9{c9 .} => -5r1c7
Single(s): 5r1c1, 9r1c3, 3r8c3, 1r4c3, 8r9c3
whip[4]: c2n3{r1 r6}- r6c5{n3 n4}- r8n4{c5 c9}- c7n4{r9 .} => -3r1c7
whip[9]: r5c7{n1 n5}- r2n5{c7 c9}- r2n6{c9 c8}- c8n8{r2 r1}- r1c5{n8 n1}- r1c7{n1 n4}- r3c9{n4 n1}- r2n1{c9 c1}- r7n1{c1 .} => -1r5c8
STTE

[totuan]

As eleven noticed, many way to solve... My path for this one:

Hidden Text: Show

Code: Select all

 *--------------------------------------------------------------------------------------*
 | 13589    1348     1389     | 67       18       67       | 1345     1348     2        |
 | 1358     2        7        | 9        18       4        | 135      1368     1568     |
 | 18       148      6        |*23       5       *23       | 7        9        148      |
 |----------------------------+----------------------------+----------------------------|
 | 1237     9        123      | 8       #234      235      | 6        147      1457     |
 | 4        168      128      | 256      7       %2569     | 159      18       3        |
 | 3678     3678     5        |#346     #349      1        |#49       2        4789     |
 |----------------------------+----------------------------+----------------------------|
 | 12379    5        4        |*23+7     6       *23+79    | 8        137      179      |
 | 3679     367      39       | 1       &349      8        | 2        5        4679     |
 | 1236789  13678    12389    | 2345-7  &2349     235-79   | 1349     13467    14679    |
 *--------------------------------------------------------------------------------------*

UR(23)r37c46 => (7)r7c46=(9)r7c6
01: (7)r7c46==(9)r7c6-r5c6=(49)r6c457,r4c5-(49=23)r89c5 => r9c46<>79

Hidden Text: Show

Code: Select all

 *--------------------------------------------------------------------------------------*
 | 13589    1348     1389     | 67       18       67       | 1345     1348     2        |
 | 1358     2        7        | 9        18       4        | 135      1368     1568     |
 | 18       148      6        | 23       5        23       | 7        9        148      |
 |----------------------------+----------------------------+----------------------------|
 | 1237     9        123      | 8        234      235      | 6        147      1457     |
 | 4        168      128      | 256      7       a69       |b159      18       3        |
 | 3678     3678     5        | 346      349      1        |b49       2        4789     |
 |----------------------------+----------------------------+----------------------------|
 | 1239     5        4        | 237      6        7-9      | 8       c13      d19       |
 | 3679     367      39       | 1        349      8        | 2        5        4679     |
 | 1236789  13678    12389    | 2345     2349     235      |c1349     13467    14679    |
 *--------------------------------------------------------------------------------------*

02: (9)r5c6=(49)r56c7-(49=13)r9c7,r7c8-(1=9)r7c9 => r7c6<>9, some singles

Hidden Text: Show

Code: Select all

 *--------------------------------------------------------------------------------------*
 | 13589    1348     1389     | 7        18       6        | 1345     1348     2        |
 | 1358     2        7        | 9        18       4        | 135      1368     1568     |
 | 18       148      6        | 23       5        23       | 7        9        148      |
 |----------------------------+----------------------------+----------------------------|
 | 137      9        13       | 8       b234      235      | 6        147      1457     |
 | 4        168      2        | 56       7        9        | 15       18       3        |
 | 3678     3678     5        |a46      a34       1        |h9-4      2       g4789     |
 |----------------------------+----------------------------+----------------------------|
 |e1239     5        4        | 23       6        7        | 8        13      f19       |
 | 3679     367      39       | 1        349      8        | 2        5        4679     |
 |d1236789  13678    1389     | 45      c2349     235      | 1349     13467    14679    |
 *--------------------------------------------------------------------------------------*

03: (4)r6c45=(4-2)r4c5=r9c5-r9c1=(2-9)r7c1=r9c7-r6c9=r6c7 => r6c7<>4, r6c7=9

Hidden Text: Show

Code: Select all

 *--------------------------------------------------------------------------------------*
 | 13589    1348     1389     | 7        18       6        |e134-5    1348     2        |
 | 1358     2        7        | 9        18       4        | 135      1368     1568     |
 | 18       148      6        | 23       5        23       | 7        9        148      |
 |----------------------------+----------------------------+----------------------------|
 | 137      9        13       | 8        234      235      | 6        147      1457     |
 | 4        168      2        |b56       7        9        |a15       18       3        |
 | 3678     3678     5        | 46       34       1        | 9        2        478      |
 |----------------------------+----------------------------+----------------------------|
 | 1239     5        4        | 23       6        7        | 8        13       19       |
 | 3679     367      39       | 1        349      8        | 2        5        4679     |
 | 1236789  13678    1389     |c45       2349     235      |d134      13467    14679    |
 *--------------------------------------------------------------------------------------*

04: (5)r5c7=r5c4-(5=4)r9c4-r9c7=r1c7 => r1c7<>5, some singles

Hidden Text: Show

Code: Select all

 *--------------------------------------------------------------------*
 | 5      1348   9      | 7      18     6      | 134    1348   2      |
 | 138    2      7      | 9      18     4      | 135    1368   1568   |
 | 18     148    6      | 23     5      23     | 7      9      148    |
 |----------------------+----------------------+----------------------|
 | 37     9      1      | 8      234    235    | 6      47     457    |
 | 4      6-8    2      | 56     7      9      | 15     18     3      |
 |*67+38 *67+38  5      | 46     34     1      | 9      2      478    |
 |----------------------+----------------------+----------------------|
 | 129    5      4      | 23     6      7      | 8      13     19     |
 |*67+9  *67     3      | 1      49     8      | 2      5      4679   |
 | 12679  67+1   8      | 45     2349   235    | 134    13467  14679  |
 *--------------------------------------------------------------------*

Look at:
- UR(67)r68c12 => (8)r6c12=(3)r6c12=(9)r8c1
- To avoid emty cells on (13678)r5689c2 => (3)r6c2=(1)r9c2
=> if r6c12<>38 then both 9r8c1 & 1r9c2 must be true
05: (6)r5c2=r5c4-(46=3)r6c45-(3)r6c12==(8|19)r6c12*,r8c1,r9c2-(19=2)r7c1-(23=1)r7c48-(1=8)r5c7 => r5c2<>8, stte

Thanks for the puzzle!
totuan

[Mauriès Robert]

Nice DEFISE resolution, especially with the first whip which speeds up the resolution.
For my part I did not see this elimination which required with my resolution mode that I take the anti-track (-9r6c7, -9r5c6)=>4r6c7->4r9c4->5r9c6->9r7c6->7r7c4->1r7c9->3r7c8->9r9c7->...
Thanks also Eleven and Totuan for your proposal of a solution using UR 23, which for my part I wanted to avoid.
Robert

[Cenoman]

A solution, w/o memory chains and w/o uniqueness, with a complex first step (as others), and five finishing AIC steps,

Code: Select all

 +----------------------------+-------------------------+--------------------------+
 |  13589     1348    1389    |  67      18     67      |   1345   1348    2       |
 |  1358      2       7       |  9       18     4       |   135    1368    1568    |
 |  18        148     6       |  23      5      23      |   7      9       148     |
 +----------------------------+-------------------------+--------------------------+
 |  1237      9       123     |  8      d234    235     |   6    Be147   Ce1457    |
 |  4         168     128     |  256     7      2569    |  C15-9  B18      3       |
 |  3678      3678    5       | y346     349    1       |Zzf49     2       4789    |
 +----------------------------+-------------------------+--------------------------+
 |  12379     5       4       |wb237     6    wb2379    |   8   vAb137    b179     |
 |  3679      367     39      |  1       349    8       |   2      5       4679    |
 |  1236789   13678   12389   | x23457  c2349  x23579   | Za1349   13467   14679   |
 +----------------------------+-------------------------+--------------------------+

Look at AALS's r69c7 & r7c8. They are linked by RCs 1,3 => freedom degree of the chain = 2 (3 digits can't be simultaneously false in any 3-subset from {1,3,4,7,9})

1. Kraken AALS-chain (13479)r69c7,r7c8
(1)r9c7 - (1=3792)r7c4689 - r9c5 = (2-4)r4c5 = r4c89 - (4=9)r6c7
(1)r7c8 - r45c8 = (15)b6p34
(7)r7c8 - r7c46 = (75-4)r9c46 = r6c4 - (4=9)r6c7
(9)r69c7
=> -9r5c7; lcls, 4 placements

Code: Select all

 +---------------------------+---------------------+-------------------------+
 |  13589     1348    1389   |  7    18     6      | A134-5  1348    2       |
 |  1358      2       7      |  9    18     4      |  135    1368    1568    |
 |  18        148     6      |  23   5      23     |  7      9       148     |
 +---------------------------+---------------------+-------------------------+
 |  137       9       13     |  8   d234    235    |  6      147     1457    |
 |  4         168     2      | D56   7      9      | E15     18      3       |
 |  3678      3678    5      | d46  d34     1      | f49     2       478-9   |
 +---------------------------+---------------------+-------------------------+
 | b12379     5       4      |  23   6      237    |  8      137    a179     |
 |  3679      367     39     |  1    349    8      |  2      5       4679    |
 | b1236789   13678   1389   | C45  c2349   2357   | B134-9  13467   14679   |
 +---------------------------+---------------------+-------------------------+

2. (9)r7c9 = (92)r79c1 - r9c5 = (2-4)r4c5 = r6c45 - (4=9)r6c7 => -9 r6c9, r9c7; 1 placement (+9r6c7)
3. (4)r1c7 = r9c7 - (4=5)r9c4 - r5c4 = (5)r5c7 => -5 r1c7; 5 placements

Code: Select all

 +----------------------+---------------------+------------------------+
 |  5     Bb1348   9    |  7    18     6      | x134   1348    2       |
 | C138     2      7    |  9    18     4      |xD135   1368    1568    |
 | C18     a148    6    |  23   5      23     |  7     9      w18-4    |
 +----------------------+---------------------+------------------------+
 |  37      9      1    |  8    234    235    |  6     47      457     |
 |  4       68     2    |  56   7      9      |yD15   z18      3       |
 |  3678   b3678   5    |  46  c34     1      |  9     2       47-8    |
 +----------------------+---------------------+------------------------+
 |  1279    5      4    |  23   6      237    |  8     137     179     |
 |  679     67     3    |  1   d49     8      |  2     5      e4679    |
 |  12679  A167    8    |  45   2349   2357   |  34-1  13467   14679   |
 +----------------------+---------------------+------------------------+

4. (4)r3c2 = (43)r16c2 - (3=4)r6c5 - r8c5 = (4)r8c9 => -4 r3c9; 1 placement (+4r3c2)
5. (1)r9c2 = r1c2 - (1=83)r23c1 - (3=51)r25c7 => -1 r9c7
enabling the finish W-Wing:
6. (8=1)r3c9 - r12c7 = r5c7 - (1=8)r5c8 => -8 r6c9; ste

[Mauriès Robert]

Hi Cenoman,
Original elimination of 9r6c7 by this Kraken which corresponds to the anti-track (-9r69c7, -1r9c7, -17r7c8) => 4r6c7-> 3r9c7->... r7c8 empty. Still had to see it, bravo !
Robert

[eleven]

...with a complex first step ...

Just to mention it: My "complex move" above can be simplified this way and also works with the starting grid (making my two first steps unnecessary):
9r5c6 = 94r56c7 - r6c4,r5c6 = 49r46c5 - (4|9=23)r89c5 - (2|3=79)r7c46 - (7|9=13)r7c89 - (1|3=49)r96c7 => -9r5c7

[Cenoman]

9r5c6 = 94r56c7 - r6c4,r5c6 = 49r46c5 - (4|9=23)r89c5 - (2|3=79)r7c46 - (7|9=13)r7c89 - (1|3=49)r96c7 => -9r5c7

...or even a bit simpler:
49r6c47|9r5c6 = 49r46c5 - (4|9=23)r89c5 - (2|3=79)r7c46 - (7|9=13)r7c89 - (1|3=49)r96c7 => -9r5c7 (one strong link less, avoiding to involve the target in the chain) ?

[eleven]

Just a remark to "avoiding to use a UR". The only one manual solver i know of, who is avoiding to use a UR is my wife, when she solves newspaper puzzles. Her argument is not, that the puzzle could have multiple solutions, but that the creator did not intend to use it, and she wants to show, that she is able to solve it in his sense