The New Sudoku Players' Forum

[Mauriès Robert]

Hi all,
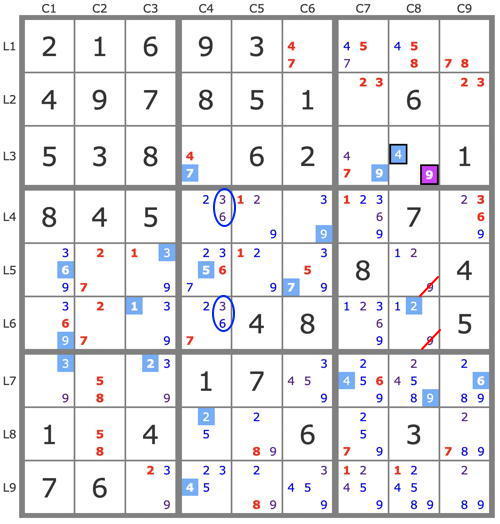
This is the puzzle I propose to solve.

2..93......7.51.6..3...2..18.5....7.......8.4....4...5...17....1.4..6.3..6.......

puzzle: Show

Robert

[Cenoman]

Code: Select all

 +-------------------+-----------------------+--------------------------+
 |  2     1    6     |  9       3     47     |  457     458      78     |
 |  4     9    7     |  8       5     1      |  23      6        23     |
 |  5     3    8     |ed47      6     2      |  479    c49       1      |
 +-------------------+-----------------------+--------------------------+
 |  8     4    5     |  236     129   39     |  12369   7        2369   |
 |  369  h27  h139   |  23567  h129   3579   |  8     hc129      4      |
 |  369  g27   139   | f2367    4     8      |  12369  c129      5      |
 +-------------------+-----------------------+--------------------------+
 |  39    58   239   |  1       7     3459   |  24569   24589    2689   |
 |  1     58   4     |  25      289   6      |  2579    3        2789   |
 |  7     6   i239   |e*2345   i289   3459   | a15-249 b124589  i289    |
 +-------------------+-----------------------+--------------------------+

1. (1)r9c7 = r9c8 - (1=294)r356c8 - r3c4 = (4r9c4* & 7r3c4) - (7)r6c4 = r6c2 - (7=1293)r5c2358 - (3=829)r9c359 => -29, -4* r9c7

Code: Select all

 +-------------------+-----------------------+--------------------------+
 |  2     1    6     |  9       3    e47*    |  457*    458      78*    |
 |  4     9    7     |  8       5     1      |  23      6        23     |
 |  5     3    8     | f47      6     2      | B479   Cf49       1      |
 +-------------------+-----------------------+--------------------------+
 |  8     4    5     |  236     129   39     |  12369   7        2369   |
 |  369   27   139   | c23567   129  d3579   |  8     Df129      4      |
 |  369   27   139   |  2367    4     8      |  12369 Df129      5      |
 +-------------------+-----------------------+--------------------------+
 |  39    58   239   |  1       7     3459   |  24569   24589    2689   |
 |  1     58   4     | b25      289   6      |Aa2579*   3        2789*  |
 |  7     6    239   |  2345    289   3459   |Fh1-5   Eg124589   289    |
 +-------------------+-----------------------+--------------------------+

2. Almost-almost ALS W-Wing:
[(5=7)r8c7 - r8c9 = r1c9 - (7=45)r1c67]
(2)r8c7-(2=5)r8c4-r5c4=(5-7)r5c6=r1c6-(7=491)r356c8-r9c8=(1)r9c7
(9)r8c7-r3c7=r3c8-(9=21)r56c8-r9c8=(1)r9c7
=> -5 r9c7; 2 placements

Code: Select all

 +-------------------+-----------------------+-------------------------+
 |  2     1    6     |  9       3     47     |  457     458     78     |
 |  4     9    7     |  8       5     1      |  23      6       23     |
 |  5     3    8     | d47      6     2      |  479    e49      1      |
 +-------------------+-----------------------+-------------------------+
 |  8     4    5     | g236     1     39     | f2369    7      f2369   |
 |  369  a27   139   |  23567   9-2   3579   |  8      e129     4      |
 |  369  b27   139   | c2367    4     8      |  2369   e129     5      |
 +-------------------+-----------------------+-------------------------+
 |  39    58   239   |  1       7     3459   |  24569   24589   2689   |
 |  1     58   4     |  25      289   6      |  2579    3       2789   |
 |  7     6    239   |  2345    289   3459   |  1       24589   289    |
 +-------------------+-----------------------+-------------------------+

3. (2=7)r5c2 - r6c2 = r6c4 - (7=4)r3c4 - (4=192)r356c8 - r4c79 = (2)r4c4 => -2 r5c5; ste

[P.O.]

Code: Select all

after basics:

2       1       6       9       3       47      457      458     78               
4       9       7       8       5       1       23       6       23               
5       3       8       47      6       2       479      49      1               
8       4       5       236     129     39      12369    7       2369             
369     27      139     ×23567  1×29    3579    8        129     4               
369     27      139     2367    4       8       12369    129     5               
39      58      239     1       7       3459    24569    24589   2689             
1       58      4       25      289     6       2579     3       2789             
7       6       239     2345    289     3459    1×(2459) 124589  289             

r3c8n49 => r5c45 <> 2 r9c7 <> 2,4,5,9

r5c45 <> 2 :
 r3c8=4 - r3c4{n4 n7} - c6n7{r1 r5} - r5c2{n7 n2}
 r3c8=9 - c8{r56}{n12} - r4n2{c79 c45}

r9c7 <> 2,4,5,9 :
 r3c8=4 - r3c4{n4 n7} - c6n7{r1 r5} - r5c2{n7 n2} - r5{c358}{n139} - r9{c359}{n289}
        - c4n4{r3 r9}
        - r3c4{n4 n7} - c6n7{r1 r5} - r5n5{c6 c4} - r8c4{n5 n2} - c7{r138}{n579}
        - r3c4{n7 n4} - r3c7{n4n7 n9}
 r3c8=9 - c8{r56}{n12} - r9n1{c8 c7}

ste.


[Mauriès Robert]

Hi all,
After reducing the puzzle using the basic techniques,
(-9r3c8) => 4r3c8->...->9r7c8 => -9r56c8, btte. Indeed:

Code: Select all

                             
[4r3c8->9r3c7->7r3c4->4r9c4]->(4r7c7->6r7c9)--------------------------------------------------
                  \                                                                           \
                    ->[7r5c6->5r5c4->(6r5c1 & 2r8c4)]->36r46c4->9r4c6.                         \
                                         \           \                                          \
                                          \           ->[(3r5c3->9r6c1)->(1r6c3 & 3r7c1)]->2r6c8->2r7c3->9r7c8->...
                                           \                   /
                                             -----------------


[DEFISE]

Single(s): 6r1c3, 1r1c2, 4r4c2, 5r3c1, 4r2c1, 8r2c4, 9r2c2, 8r3c3, 6r3c5, 8r6c6
Naked pairs: 27c2r56 => -2r7c2 -2r8c2 -7r8c2
Single(s): 7r9c1
Box/Line: 2c2b4 => -2r5c3 -2r6c3
whip[6]: c2n2{r5 r6}- r6n7{c2 c4}- r3c4{n7 n4}- r3c8{n4 n9}- r5c8{n9 n1}- r6c8{n1 .} => -2r5c5
whip[8]: r5c5{n1 n9}- r4c6{n9 n3}- r5n3{c6 c1}- r7n3{c1 c3}- c3n2{r7 r9}- r9c5{n2 n8}- r9c9{n8 n9}- r8n9{c9 .} => -1r5c3
Single(s): 1r6c3
whip[4]: r3c4{n7 n4}- r3c8{n4 n9}- r6c8{n9 n2}- r6c2{n2 .} => -7r6c4
Single(s): 7r6c2, 2r5c2
Naked pairs: 19r5c58 => -9r5c1 -9r5c3 -9r5c6
Single(s): 3r5c3, 6r5c1, 9r6c1, 2r6c8, 3r7c1
whip[6]: r5n9{c5 c8}- r3c8{n9 n4}- r1n4{c8 c6}- r7c6{n4 n5}- r7c2{n5 n8}- r7c8{n8 .} => -9r4c6
STTE

[m_b_metcalf]

Or, backdoor 2r4c4.

Mike

[Mauriès Robert]

Or, backdoor 2r4c4.

Hi Mike,
Yes 2r4c4 is a backdoor, but by choosing to develop the anti-track I am showing that we are eliminating 9r56c8 which leads to the validation of 2r4c4.
Robert