The New Sudoku Players' Forum

by **Mauriès Robert** » Mon Jan 24, 2022 9:52 am

Hi all,
I propose you this easier puzzle than the previous one.
I will give my resolution in the thread a little later, addressing myself more particularly to Denis.
Good resolution.
Robert

.2.....3...7.5.2..1..2.6..9.78...35.3..879..4............5.2...24.....85..6.1.9..

puzzle: Show

by **yzfwsf** » Mon Jan 24, 2022 10:38 am

Single and Locked Candidates go here

Code: Select all: .-----------------.-------------------.--------------------. | 4568 2 459 | 1479 489 1478 | 14568 3 168 | | 468 3689 7 | 1349 5 1348 | 2 146 168 | | 1 358 345 | 2 348 6 | 4578 47 9 | :-----------------+-------------------+--------------------: | 9 7 8 | 146 246 14 | 3 5 126 | | 3 156 125 | 8 7 9 | 16 126 4 | | 46 16 124 | 136 236 5 | 1678 9 12678 | :-----------------+-------------------+--------------------: | 78 1389 139 | 5 34689 2 | 1467 1467 1367 | | 2 4 139 | 3679 369 37 | 167 8 5 | | 578 358 6 | 347 1 3478 | 9 247 237 | '-----------------'-------------------'--------------------'

Dynamic Contradiction Chain: If r9c2=5 Then r2c2=3 And r2c2<>3 simultaneously,so r9c2<>5

Hidden Text: Show

Single and Locked Candidates

Code: Select all: .----------------.-------------------.-------------------. | 468 2 459 | 1479 489 1478 | 14568 3 168 | | 468 369 7 | 1349 5 1348 | 2 146 168 | | 1 35 345 | 2 348 6 | 4578 47 9 | :----------------+-------------------+-------------------: | 9 7 8 | 146 246 14 | 3 5 126 | | 3 156 125 | 8 7 9 | 16 126 4 | | 46 16 124 | 136 236 5 | 1678 9 12678 | :----------------+-------------------+-------------------: | 7 1389 139 | 5 34689 2 | 146 146 136 | | 2 4 139 | 3679 369 37 | 167 8 5 | | 5 38 6 | 347 1 3478 | 9 247 237 | '----------------'-------------------'-------------------'

Region Forcing Chain: Each 3 in c5 true in turn will all lead to: r7c5<>8

Hidden Text: Show

stte

Website · by **denis_berthier** » Mon Jan 24, 2022 11:33 am

Mauriès Robert wrote:I will give my resolution in the thread a little later, addressing myself more particularly to Denis.
.2.....3...7.5.2..1..2.6..9.78...35.3..879..4............5.2...24.....85..6.1.9..

Thanks for the particular attention. But, IMO, you'd better spend time answering my question about what a TR is here: http://forum.enjoysudoku.com/is-there-any-original-theory-or-any-theory-at-all-in-tdp-t39766.html. Your whole TDP theory is on the verge of crumbling down.

SER = 9.0

Code: Select all: Resolution state after Singles and whips[1]: +-------------------+-------------------+-------------------+ ! 4568 2 459 ! 1479 489 1478 ! 14568 3 168 ! ! 468 3689 7 ! 1349 5 1348 ! 2 146 168 ! ! 1 358 345 ! 2 348 6 ! 4578 47 9 ! +-------------------+-------------------+-------------------+ ! 9 7 8 ! 146 246 14 ! 3 5 126 ! ! 3 156 125 ! 8 7 9 ! 16 126 4 ! ! 46 16 124 ! 136 236 5 ! 1678 9 12678 ! +-------------------+-------------------+-------------------+ ! 78 1389 139 ! 5 34689 2 ! 1467 1467 1367 ! ! 2 4 139 ! 3679 369 37 ! 167 8 5 ! ! 578 358 6 ! 347 1 3478 ! 9 247 237 ! +-------------------+-------------------+-------------------+ 166 candidates

Single-step solution with tracks in the form of Forcing-TE

Code: Select all: FORCING[3]-T&E(W1) applied to trivalue candidates n3r9c2, n5r9c2 and n8r9c2 : ===> 8 values decided in the three cases: n3r7c9 n2r4c5 n4r6c1 n9r1c5 n9r8c4 n7r3c8 n6r8c5 n3r6c5 ===> 62 candidates eliminated in the three cases: n4r1c1 n5r1c3 n9r1c3 n4r1c4 n9r1c4 n4r1c5 n8r1c5 n4r1c6 n8r1c6 n1r1c7 n6r1c7 n8r1c7 n1r1c9 n4r2c1 n3r2c2 n1r2c4 n9r2c4 n1r2c6 n6r2c9 n8r2c9 n8r3c2 n3r3c5 n7r3c7 n4r3c8 n4r4c5 n6r4c5 n2r4c9 n1r5c3 n6r5c8 n6r6c1 n4r6c3 n3r6c4 n2r6c5 n6r6c5 n1r6c7 n6r6c7 n1r6c9 n2r6c9 n6r6c9 n3r7c2 n3r7c3 n3r7c5 n6r7c5 n9r7c5 n1r7c7 n4r7c8 n7r7c8 n1r7c9 n6r7c9 n7r7c9 n9r8c3 n3r8c4 n6r8c4 n7r8c4 n3r8c5 n9r8c5 n6r8c7 n8r9c1 n4r9c6 n7r9c6 n7r9c8 n3r9c9 stte

Of course, this is not the best way of solving in SudoRules (there's a solution in W8).

by **P.O.** » Mon Jan 24, 2022 3:57 pm

Code: Select all: after singles and intersections and a hidden pair: r6{c7c9}{n7n8} => r6c7 r6c9 <> 1,2,6 4568 2 459 1479 489 1478 14568 3 168 468 3689 7 1349 5 1348 2 146 168 1 358 345 2 348 6 4578 47 9 9 7 8 146 246 14 3 5 126 3 156 125 8 7 9 16 126 4 46 16 124 136 236 5 78 9 78 78 1389 139 5 34689 2 1467 146×7 3×(167) 2 4 139 3679 369 37 167 8 5 578 358 6 347 1 3478 9 247 237 c9n3{r7 r9} - c9n2{r9 r4} - r5n2{c8 c3} - r5n5{c3 c2} - r9c2{n3n5 n8} - b8n8{r9c6 r7c5} - r3n8{c5 c7} - c9{r1r2}{n1n6} => r7c9 <> 1,6 c1n7{r7 r9} - r9n5{c1 c2} - r5{c2c7c8}{n1n2n6} - r9c8{n2n7 n4} - c7{r5r7r8}{n1n6n7} => r7c8 r7c9 <> 7 single: ( r7c9b9 n3 ) 4×568 2 459 1479 489 1478 14568 3 168 468 3689 7 1349 5 1348 2 146 168 1 358 345 2 348 6 4578 47 9 9 7 8 146 246 14 3 5 126 3 156 125 8 7 9 16 126 4 46 16 124 136 ×236 5 78 9 78 78 189 19 5 4689 2 1467 146 3 2 4 139 3679 369 37 167 8 5 578 358 6 347 1 3478 9 247 27 c3n2{r6 r5} - r5n5{c3 c2} - r9n5{c2 c1} - c1n7{r9 r7} - c1n8{r7 r1r2} - r3c2{n5n8 n3} - c3n3{r3 r8} - c5n3{r8 r6} => r6c5 <> 2 r9n5{r1 r2} - b7n3{r9c2 r8c3} - r8n1{c3 c7} - r5c7{n1 n6} - r5c2{n5n6 n1} - b6n1{r5c8 r4c9} - r4{c4c6}{n4n6} - r8{c4c6}{n7n9} - c5n9{c7c8 c1} - c3{r1r3}{n4n5} => r1c1 <> 5 singles + 2 intersections. ste.

by **DEFISE** » Mon Jan 24, 2022 5:40 pm

Solution 1

Hidden Text: Show

Single(s): 9r4c1, 9r6c8, 5r6c6
Box/Line: 7r3b3 => -7r1c7 -7r1c9
Box/Line: 4r4b5 => -4r6c4 -4r6c5
Hidden pairs: 78r6c79 => -1r6c7 -6r6c7 -1r6c9 -2r6c9 -6r6c9

Code: Select all: |-----------------------------------------------------------| | 4568 2 459 | 1479 489 1478 | 14568 3 168 | | 468 3689 7 | 1349 5 1348 | 2 146 168 | | 1 358 345 | 2 348 6 | 4578 47 9 | |-----------------------------------------------------------| | 9 7 8 | 146 246 14 | 3 5 126 | | 3 156 125 | 8 7 9 | 16 126 4 | | 46 16 124 | 136 236 5 | 78 9 78 | |-----------------------------------------------------------| | 78 1389 139 | 5 34689 2 | 1467 1467 1367 | | 2 4 139 | 3679 369 37 | 167 8 5 | | 578 358 6 | 347 1 3478 | 9 247 237 | |-----------------------------------------------------------|

whip[9]: r9n2{c9 c8}- r5n2{c8 c3}- r5n5{c3 c2}- r9c2{n5 n8}- r7c1{n8 n7}- r7n8{c1 c5}- r3n8{c5 c7}- r6c7{n8 n7}- c9n7{r6 .}
=> -3r9c9
Single(s): 3r7c9

whip[8]: r6c2{n6 n1}- c2n6{r6 r2}- c2n9{r2 r7}- r7c3{n9 n1}- r8c3{n1 n3}- b1n3{r3c3 r3c2}- c5n3{r3 r6}- r6c4{n3 .} => -6r6c1
Single(s): 4r6c1
Box/Line: 6c1b1 => -6r2c2

whip[6]: r6c3{n2 n1}- r7c3{n1 n9}- r8c3{n9 n3}- c5n3{r8 r3}- r2n3{c4 c2}- c2n9{r2 .} => -2r6c5
Single(s): 2r6c3, 2r5c8, 2r4c5, 2r9c9, 7r6c9, 8r6c7
Naked pairs: 47c8r39 => -4r2c8 -4r7c8 -7r7c8
Box/Line: 4r2b2 => -4r1c4 -4r1c5 -4r1c6 -4r3c5
Single(s): 4r7c5, 4r9c8, 7r3c8, 8r9c6

Code: Select all: |--------------------------------------------------| | 568 2 459 | 179 89 17 | 1456 3 168 | | 68 389 7 | 1349 5 134 | 2 16 168 | | 1 358 345 | 2 38 6 | 45 7 9 | |--------------------------------------------------| | 9 7 8 | 146 2 14 | 3 5 16 | | 3 156 15 | 8 7 9 | 16 2 4 | | 4 16 2 | 136 36 5 | 8 9 7 | |--------------------------------------------------| | 78 189 19 | 5 4 2 | 167 16 3 | | 2 4 139 | 3679 369 37 | 167 8 5 | | 57 35 6 | 37 1 8 | 9 4 2 | |--------------------------------------------------|

whip[3]: r3c5{n8 n3}- c3n3{r3 r8}- c6n3{r8 .} => -8r1c5
STTE

Solution 2

Hidden Text: Show

by **eleven** » Mon Jan 24, 2022 10:31 pm

Could not find less complex chains, which would progress the puzzle. I reused a part in the second chain.
Normally i don't solve such puzzles, where i don't find anything interesting, but i'm curious to compare, how Robert did it.

Code: Select all: +-----------------------+----------------------+----------------------+ | c4568 2 459 | 1479 489 1478 | 14568 3 168 | | c468 ig3689 7 |h1349 5 h1348 | 2 146 168 | | 1 jd358 345 | 2 348 6 | 4578 47 9 | +-----------------------+----------------------+----------------------+ | 9 7 8 | 146 246 14 | 3 5 126 | | 3 ba16+5 125 | 8 7 9 | 16 126 4 | | b46 ba16 124 |*136 236 5 | 78 9 78 | +-----------------------+----------------------+----------------------+ | e78 e1389 139 | 5 f34689 2 | 1467 1467 1367 | | 2 4 139 | 3679 369 g37 | 167 8 5 | | b578 jd358 6 |g347 1 g3478 | 9 247 237 | +-----------------------+----------------------+----------------------+

6r45c2 = [5r5c2-r9c2=5r9c1] & 61*3r6c124 - [(5=38)r39c2 & (5|6=48)r12c1] - 8r7c12 = 8r7c5 - (8r9c6|*3r9c4) = (347r89c6 & 47r9c4) - 3r2c*46 = 3r2c2 - (3=58r39c2) - (5=16)r45c2 => -6r6c1

Code: Select all: *-----------------------------------------------------------------------* | 568 2 459 | 1479 489 1478 | 14568 3 168 | | 68 i389 7 | h1349 5 h1348 | 2 146 168 | | 1 d358 345 | 2 348 6 | 4578 47 9 | |---------------------+------------------------+------------------------| | 9 7 8 | 146 a246 14 | 3 5 126 | | 3 b156 b125 | 8 7 9 | 16 126 4 | | 4 16 12 | *136 b236 5 | 78 9 78 | |---------------------+------------------------+------------------------| | 78 e1389 139 | 5 f34689 2 | 1467 1467 1367 | | 2 4 139 | 3679 369 g37 | 167 8 5 | | 578 d358 6 | g347 1 g3478 | 9 247 237 | *-----------------------------------------------------------------------*

2r4c5 = 2*3r6c56 & 25r5c32 - (5=38)r39c2 - 8r7c2 = 8r7c5 - (8r9c6|*3r9c4) = (347r89c6 & 47r9c4) - 3r2c*46 = 3r2c2 - (3=58r39c2) - 5r5c2 = (5-2)r5c3 = 2r5c4 => -2r6c5
basics ..

Code: Select all: *-----------------------------------------------------------* | 568 2 459 | 17 9-8 17 | 45 3 a68 | | 68 39 7 | 349 5 c34 | 2 16 168 | | 1 358 345 | 2 d38 6 | 45 7 9 | |--------------------+------------------+-------------------| | 9 7 8 | 146 2 c14 | 3 5 b16 | | 3 156 15 | 8 7 9 | 16 2 4 | | 4 16 2 | 136 36 5 | 8 9 7 | |--------------------+------------------+-------------------| | 78 189 19 | 5 4 2 | 167 16 3 | | 2 4 13 | 69 69 37 | 17 8 5 | | 57 35 6 | 37 1 8 | 9 4 2 | *-----------------------------------------------------------*

(8=6)r1c9 - (6=1)r4c9 - (1=43)r42c6 - (3=8)r3c5 => -8r1c5

by **Mauriès Robert** » Mon Jan 24, 2022 11:16 pm

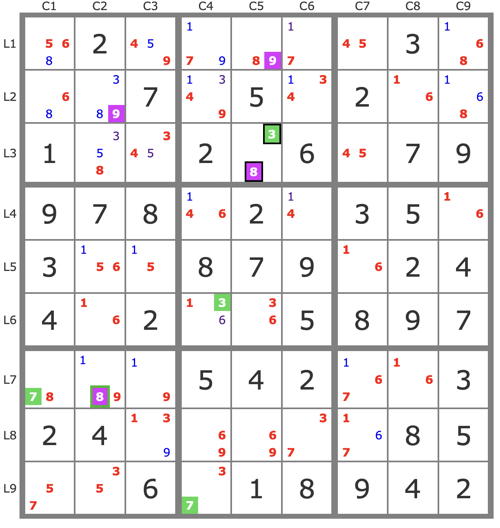
Hi all,
As I said, here is my resolution presented in several ways for Denis, hoping that he will understand how TDP can be declined and that it has nothing to do with copying his techniques.

1) We can solve with a minimum of steps by looking for invalid tracks, as follows.
I specify that here the chaining is written with a memory effect, i.e. ->A indicates that the positioning of A depends on that of the previous candidates ->.

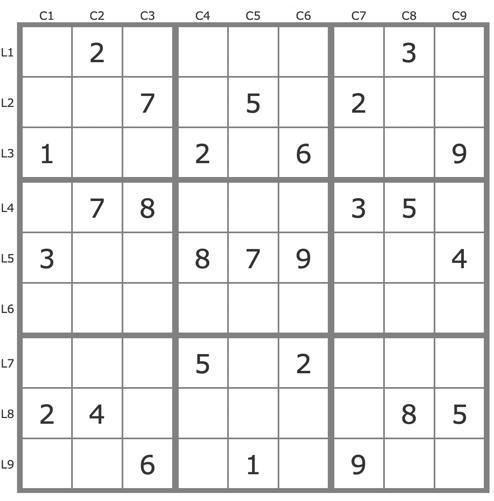
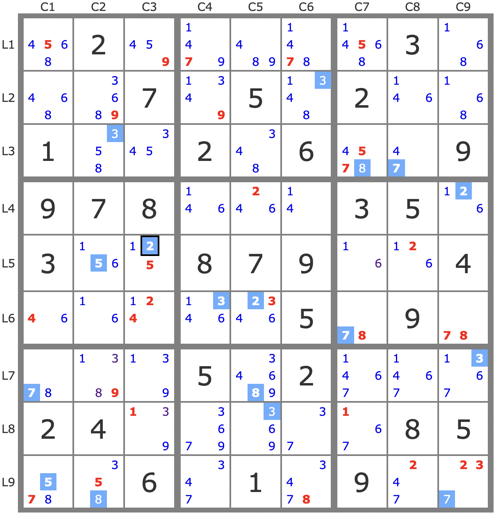
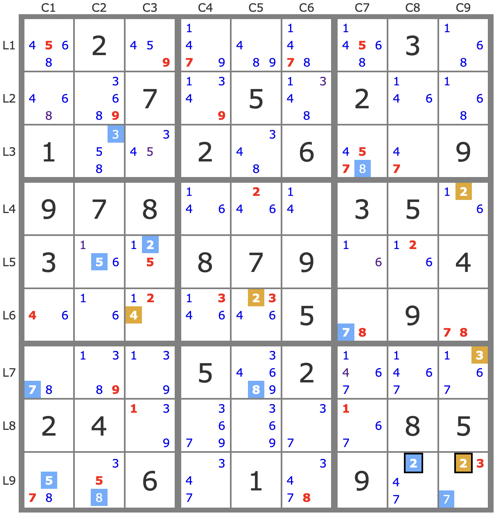
P(2r5C3) : 2r5c3->5r5c2->5r9c1->7r7c1->3r3c2->8r9c2->8r7c5->8r3c7->7r6c7->7r3c8->7r9c9->3r7c9->2r4c9->2r6c5->3r6c4->3r2c6->3r8c5->... => contradiction (no 3 possible in B7) => r6c3=6 + basic techniques (TB).

puzzle: Show

P(6r6c2) : 6r6c2->3r6c5->1r6c4->1r4c9->1r2c8->1r1c6->7r1c4->7r9c1->8r7c1->8r3c5->9r1c5->9r2c2->... = > contradiction (no 8 possible in B1) => r6c2=1 and end with TB (singles).

puzzle: Show

This method of solving is what Denis calls T&E. I only use it to determine the difficulty level of the puzzle, which I call the TDP level.
This kind of resolution has earned me criticism on this forum, which has led me to avoid it.

2) One can also solve by using conjugate tracks. This is what I sometimes do to explain to my readers how to solve in several steps that do not necessarily involve searching for invalid leads. For example, for a first step :
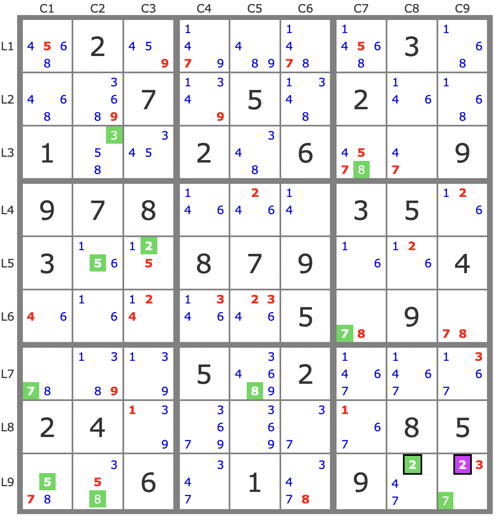
P(2r5c3) : 2r5c3->5r5c2->5r9c1->7r7c1->3r3c2->8r9c2->8r7c5->8r3c7->7r3c8->7r6c7->7r9c9->3r7c9->...
P(2r6c3) : 2r6c3->2r4c5->2r9c9->3r7c9->...
=> r7c9=3
The property used here is that any common candidate of two conjugate tracks is a solution of its cell.

puzzle: Show

But I could also have used P(2r9c9) and P(2r9c8) which are conjugate tracks, like this:
P(2r9c9) : 2r9c9->2r5c8->2r6c3->4r6c1->...
P(2r9c8) : 2r9c8->2r5c3->5r5c2->5r9c1->7r7c1->3r3c2->8r9c2->8r7c5->8r3c7->7r6c7->7r9c9->...
=> r9c9≠3 => r7c9=3.
The property used here is that any candidate who sees both a candidate from each of the conjugate tracks can be eliminated.

puzzle: Show

But I could have also, considered P(2r9c8) as the anti-track P'(2r9c9) to eliminate 3r9c9 as I usually do on this forum since 3r9c9 sees both 2r9c9 and a candidate of P'(2r9c9), developing only the anti-track.

puzzle: Show

Etc, etc ...

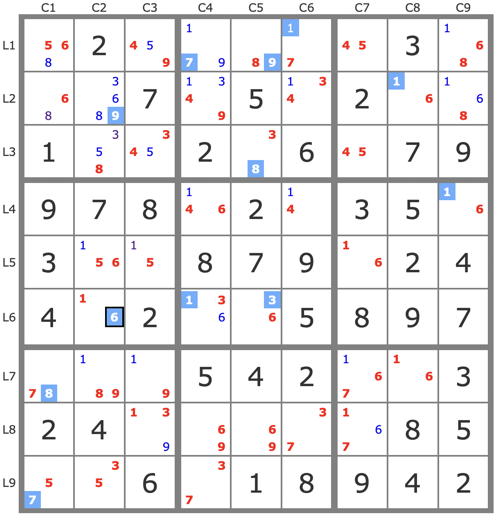
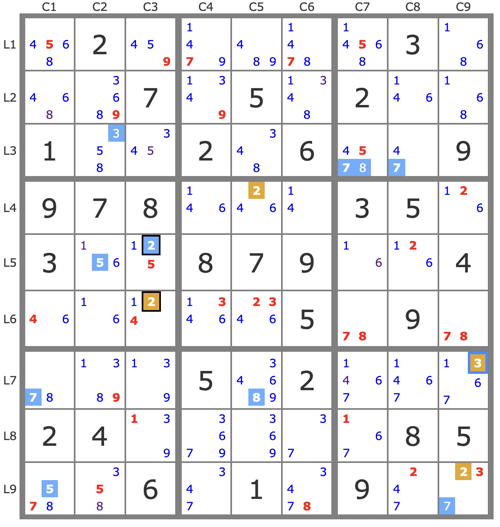
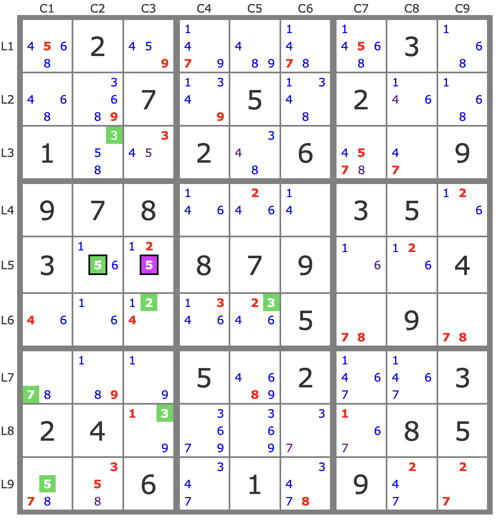
3) Here is the end of my resolution of all the resolutions I could make, after placing 3r7c9.
P'(5r5c3) : (-5r5c3) => [5r5c2->5r9c1->7r7c1->8r79c2]->3r3c2->3r8c3->3r6c5->2r6c3->.... => -2r5c3 => 2r6c3 +TB.

puzzle: Show

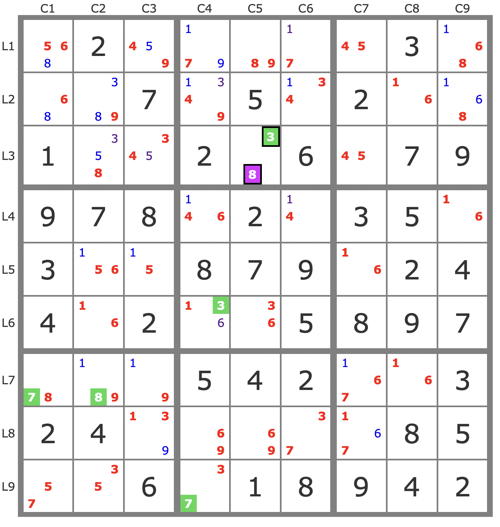
P'(8r3c5) : (-8r3c5) => 3r3c5->3r6c4->7r9c4->7r7c1->8r7c2->... => -8r3c2 => r3c5=8 , stte.

puzzle: Show

But I can also find this result with two conjugate tracks :
P(8r3c5) : [8r3c5->9r3c5-> 9r2c2]->8r7c2->...
P(3r3c5) : 3r3c5->3r6c4->7r9c4->7r7c1->8r7c2->...
=> r7c2=8 =>r2c5=8, stte

puzzle: Show

This example shows that when I study a puzzle I find different ways of solving it with TDP, but in the end, when it comes to presenting one, I only retain the simplest one and not because I have copied anyone else.
Robert

Website · by **denis_berthier** » Tue Jan 25, 2022 3:40 am

.
That's really great news: a puzzle can be solved in several different ways.

Website · by **denis_berthier** » Tue Jan 25, 2022 4:48 am

.
I've already given a 1-step solution with Forcing[3]-T&E(W1). Here is now a solution in 3 steps, using conjugated tracks.
I dont't know if 2 steps would be enough; that's not my point. My point is to show how tracks and conjugated tracks really look like if you stick to their definition: a track is the set... (i.e.in particular, it is not a sequence)

This is the full SudoRules output of Forcing-T&E(W1).
To read it as conjugated tracks, replace "49 values decided by n5r5c2" by "T(n5r5c2)" and so on.
Notice that SudoRules gives the strict content of the relevant various tracks, according to Robert's definition.
I have nevertheless also kept all the additional information about all the assertions and eliminations common to each pair of conjugated tracks.

Staring from the resolution state after whips[1]

Code: Select all: Resolution state after Singles and whips[1]: +-------------------+-------------------+-------------------+ ! 4568 2 459 ! 1479 489 1478 ! 14568 3 168 ! ! 468 3689 7 ! 1349 5 1348 ! 2 146 168 ! ! 1 358 345 ! 2 348 6 ! 4578 47 9 ! +-------------------+-------------------+-------------------+ ! 9 7 8 ! 146 246 14 ! 3 5 126 ! ! 3 156 125 ! 8 7 9 ! 16 126 4 ! ! 46 16 124 ! 136 236 5 ! 1678 9 12678 ! +-------------------+-------------------+-------------------+ ! 78 1389 139 ! 5 34689 2 ! 1467 1467 1367 ! ! 2 4 139 ! 3679 369 37 ! 167 8 5 ! ! 578 358 6 ! 347 1 3478 ! 9 247 237 ! +-------------------+-------------------+-------------------+ 166 candidates

I'm using TB = W1.

FORCING-T&E(W1) applied to bivalue candidates n5r5c2 and n5r5c3 :
.... 49 values decided by n5r5c2 : n5r5c2 n5r9c1 n7r7c1 n3r3c2 n8r9c2 n8r7c5 n4r3c5 n7r3c8 n5r3c3 n8r3c7 n9r1c5 n4r1c3 n4r6c1 n6r6c2 n9r2c2 n1r7c2 n1r8c7 n7r6c7 n6r5c7 n4r7c7 n2r9c8 n1r5c8 n2r5c3 n1r6c3 n3r6c4 n2r6c5 n8r6c9 n6r4c5 n3r8c5 n7r8c6 n4r9c6 n1r4c6 n4r4c4 n8r1c6 n3r2c6 n6r1c1 n8r2c1 n1r1c9 n6r2c9 n3r7c9 n7r9c9 n9r7c3 n4r2c8 n7r1c4 n1r2c4 n2r4c9 n6r7c8 n5r1c7 n9r8c4
.... 9 values decided by n5r5c3 : n5r5c3 n2r5c8 n2r9c9 n3r7c9 n7r6c9 n8r6c7 n2r4c5 n2r6c3 n4r6c1
===> 2 values decided in both cases: n4r6c1 n3r7c9
===> 22 candidates eliminated in both cases: n4r1c1 n5r1c3 n8r1c7 n4r2c1 n6r2c2 n4r4c5 n1r5c3 n6r5c8 n6r6c1 n4r6c3 n1r6c7 n6r6c7 n1r6c9 n2r6c9 n6r6c9 n3r7c2 n3r7c3 n3r7c5 n1r7c9 n6r7c9 n7r7c9 n3r9c9

Code: Select all: CURRENT RESOLUTION STATE: 568 2 49 1479 489 1478 1456 3 168 68 389 7 1349 5 1348 2 146 168 1 358 345 2 348 6 4578 47 9 9 7 8 146 26 14 3 5 126 3 156 25 8 7 9 16 12 4 4 16 12 136 236 5 78 9 78 78 189 19 5 4689 2 1467 1467 3 2 4 139 3679 369 37 167 8 5 578 358 6 347 1 3478 9 247 27

FORCING-T&E(W1) applied to bivalue candidates n5r3c3 and n5r5c3 :
.... 41 values decided by n5r3c3 : n5r3c3 n2r5c3 n1r6c3 n9r7c3 n3r8c3 n7r8c6 n4r1c3 n6r6c2 n3r6c4 n4r9c4 n2r6c5 n6r4c5 n9r8c5 n6r8c4 n1r8c7 n6r5c7 n5r1c7 n8r1c5 n1r1c6 n4r4c6 n3r2c6 n8r9c6 n5r9c2 n7r9c1 n2r9c9 n1r4c9 n8r7c1 n1r7c2 n6r2c1 n8r2c9 n7r6c9 n8r6c7 n9r2c2 n4r3c5 n7r3c8 n6r1c9 n7r1c4 n1r2c8 n4r7c8 n7r7c7 n3r3c2
.... 7 values decided by n5r5c3 : n5r5c3 n2r5c8 n2r9c9 n7r6c9 n8r6c7 n2r4c5 n2r6c3
===> 3 values decided in both cases: n2r9c9 n7r6c9 n8r6c7
===> 8 candidates eliminated in both cases: n8r3c7 n2r4c9 n5r5c2 n1r5c8 n7r6c7 n8r6c9 n2r9c8 n7r9c9

Code: Select all: CURRENT RESOLUTION STATE: 568 2 49 1479 489 1478 1456 3 168 68 389 7 1349 5 1348 2 146 168 1 358 345 2 348 6 457 47 9 9 7 8 146 26 14 3 5 16 3 16 25 8 7 9 16 2 4 4 16 12 136 236 5 8 9 7 78 189 19 5 4689 2 1467 1467 3 2 4 139 3679 369 37 167 8 5 578 358 6 347 1 3478 9 47 2

naked-single ==> r5c8=2
naked-single ==> r5c3=5
hidden-single-in-a-block ==> r6c3=2
hidden-single-in-a-block ==> r4c5=2
whip[1]: c3n1{r8 .} ==> r7c2≠1

FORCING-T&E(W1) applied to bivalue candidates n6r1c1 and n6r2c1 :
.... 42 values decided by n6r1c1 : n6r1c1 n8r2c1 n7r7c1 n5r9c1 n5r1c7 n5r3c2 n8r1c9 n8r3c5 n8r9c6 n3r9c2 n9r2c2 n8r7c2 n4r1c3 n3r3c3 n9r1c5 n9r8c4 n1r8c3 n9r7c3 n4r7c5 n7r9c4 n4r9c8 n7r3c8 n4r3c7 n3r8c6 n6r8c5 n7r8c7 n3r6c5 n1r1c4 n6r6c4 n1r6c2 n6r5c2 n1r5c7 n6r7c7 n1r7c8 n6r2c8 n1r2c9 n6r4c9 n4r4c4 n1r4c6 n3r2c4 n4r2c6 n7r1c6
.... 40 values decided by n6r2c1 : n6r2c1 n6r7c8 n1r2c8 n8r2c9 n6r1c9 n1r4c9 n6r5c7 n1r5c2 n6r6c2 n3r6c5 n1r6c4 n4r4c6 n6r4c4 n3r2c6 n7r8c6 n8r9c6 n1r1c6 n1r8c7 n9r2c2 n8r7c2 n7r7c1 n5r9c1 n3r9c2 n4r9c4 n7r9c8 n4r3c8 n8r3c5 n3r3c3 n5r1c7 n7r3c7 n9r7c5 n6r8c5 n3r8c4 n1r7c3 n4r1c5 n9r8c3 n5r3c2 n8r1c1 n4r7c7 n9r1c4
===> 12 values decided in both cases: n7r7c1 n5r9c1 n5r1c7 n5r3c2 n8r3c5 n8r9c6 n3r9c2 n9r2c2 n8r7c2 n3r3c3 n6r8c5 n3r6c5
===> 51 candidates eliminated in both cases: n5r1c1 n9r1c3 n4r1c4 n7r1c4 n8r1c5 n4r1c6 n8r1c6 n1r1c7 n4r1c7 n6r1c7 n1r1c9 n3r2c2 n8r2c2 n1r2c4 n4r2c4 n9r2c4 n1r2c6 n8r2c6 n4r2c8 n6r2c9 n3r3c2 n8r3c2 n4r3c3 n3r3c5 n4r3c5 n5r3c7 n1r4c4 n3r6c4 n6r6c5 n8r7c1 n9r7c2 n6r7c5 n8r7c5 n1r7c7 n7r7c7 n4r7c8 n7r7c8 n3r8c3 n6r8c4 n7r8c4 n3r8c5 n9r8c5 n6r8c7 n7r9c1 n8r9c1 n5r9c2 n8r9c2 n3r9c4 n3r9c6 n4r9c6 n7r9c6

Code: Select all: CURRENT RESOLUTION STATE: 68 2 4 19 49 17 5 3 68 68 9 7 3 5 34 2 16 18 1 5 3 2 8 6 47 47 9 9 7 8 46 2 14 3 5 16 3 16 5 8 7 9 16 2 4 4 16 2 16 3 5 8 9 7 7 8 19 5 49 2 46 16 3 2 4 19 39 6 37 17 8 5 5 3 6 47 1 8 9 47 2

stte

by **Mauriès Robert** » Tue Jan 25, 2022 7:44 am

denis_berthier wrote:.
That's really great news: a puzzle can be solved in several different ways.

No, you learn that TDP does not come in one form and that I did not need you and your theory for that contrary to what you imply on the forum.
But with your twisted mind you always make a mockery of what others write, which by dint of repetition only discredits your words and writings.
Robert

Website · by **denis_berthier** » Tue Jan 25, 2022 8:18 am

Mauriès Robert wrote:
denis_berthier wrote:.That's really great news: a puzzle can be solved in several different ways.

No, you learn that TDP does not come in one form and that I did not need you and your theory for that contrary to what you imply on the forum.

You claim that your initial inspiration for tracks was SE dynamic contradiction chains (or some other SE chain, I can't remember). I'm not debating this. What I said is, you obviously had other sources of "inspiration".

Wrt this puzzle, what I see here is, conjugated tracks, strictly used as per your definition (a track is a set of...), are Forcing-T&E (or forcing dynamic chains deprived of any chain or network structure, if you prefer this reference). Or would you claim that my solution doesn't strictly qualify as one with conjugated tracks? In this case, can you tell me what's missing?

Mauriès Robert wrote:But with your twisted mind ....

With my twisted mind (thanks for the compliment; I don't like very much too flat minds), I'm debunking the useless or false stuff in your TDP theory (see here: http://forum.enjoysudoku.com/is-there-any-original-theory-or-any-theory-at-all-in-tdp-t39766.html). You're welcome to provide input (if you can stick to technical arguments).

by **Mauriès Robert** » Tue Jan 25, 2022 10:06 am

denis_berthier wrote:... Or would you claim that my solution doesn't strictly qualify as one with conjugated tracks? In this case, can you tell me what's missing?

Hi Denis,
In order to answer you, you must first give me the definition of "FORCING-T&E(W1) applied to bivalue candidates ". Because if I understand what T&E(TB) is, I don't know what T&E(W1) is.
Robert

Website · by **denis_berthier** » Tue Jan 25, 2022 11:13 am

Mauriès Robert wrote:
denis_berthier wrote:... Or would you claim that my solution doesn't strictly qualify as one with conjugated tracks? In this case, can you tell me what's missing?

In order to answer you, you must first give me the definition of "FORCING-T&E(W1) applied to bivalue candidates ". Because if I understand what T&E(TB) is, I don't know what T&E(W1) is.

Take TB = W1

by **Mauriès Robert** » Tue Jan 25, 2022 1:18 pm

Hi Denis,
Yes, it is indeed conjugated tracks that you have used in 3 successive steps. You present it as sets, which is in accordance with my definition, but in a different way.
When I started on this forum, I was reproached for this type of presentation, which I therefore abandoned in favour of a sequential presentation A->B->C->.... (see the first part of my resolution).
Robert

Website · by **denis_berthier** » Tue Jan 25, 2022 4:10 pm

Mauriès Robert wrote:Yes, it is indeed conjugated tracks that you have used in 3 successive steps. You present it as sets, which is in accordance with my definition

Thanks; that's all I wanted you to admit. Conjugated tracks are Forcing-T&E

The New Sudoku Players' Forum

Robert's puzzles 2022-01-24

Robert's puzzles 2022-01-24

Re: Robert's puzzles 2022-01-24

Re: Robert's puzzles 2022-01-24

Re: Robert's puzzles 2022-01-24

Re: Robert's puzzles 2022-01-24

Re: Robert's puzzles 2022-01-24

Re: Robert's puzzles 2022-01-24

Re: Robert's puzzles 2022-01-24

Re: Robert's puzzles 2022-01-24

Re: Robert's puzzles 2022-01-24

Re: Robert's puzzles 2022-01-24

Re: Robert's puzzles 2022-01-24

Re: Robert's puzzles 2022-01-24

Re: Robert's puzzles 2022-01-24

Re: Robert's puzzles 2022-01-24