The New Sudoku Players' Forum

[Mauriès Robert]

Hi all,
I propose you to solve this puzzle, which does not pose any difficulties, but requires (in my opinion) at least two steps in addition to the basic techniques.
Cordialy
Robert
.19..74....7..6.8.....34..19..4.......8...7....4..1..36...4.....4.6..5....32..164

puzzle: Show

[Cenoman]

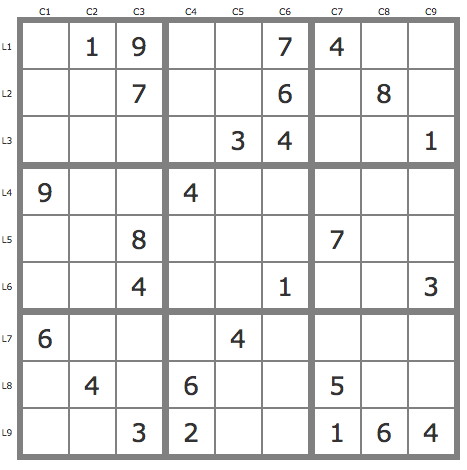
Not found reasonable two steps. So, in three steps:

Code: Select all

 +----------------------+--------------------------+----------------------+
 |  3     1       9     | C8-5      28-5    7      |  4     a25    6      |
 |  4     25      7     |  1-59     1259    6      |  3      8     259    |
 |  258   2568    256   |Cb59       3       4      | a29     7     1      |
 +----------------------+--------------------------+----------------------+
 |  9     37-256 B256   |  4       A5678   A2358   | B268    1    B258    |
 |  1     2356    8     | C359      569     259-3  |  7      4     259    |
 |  257   2567    4     |  5789     5689-7  1      |  2689   259   3      |
 +----------------------+--------------------------+----------------------+
 |  6     25789   125   | C137-589  4       3589   |  289    239   2789   |
 |  278   4       12    |  6        1789    389    |  5      239   2789   |
 |  578   5789    3     |  2        5789    589    |  1      6     4      |
 +----------------------+--------------------------+----------------------+

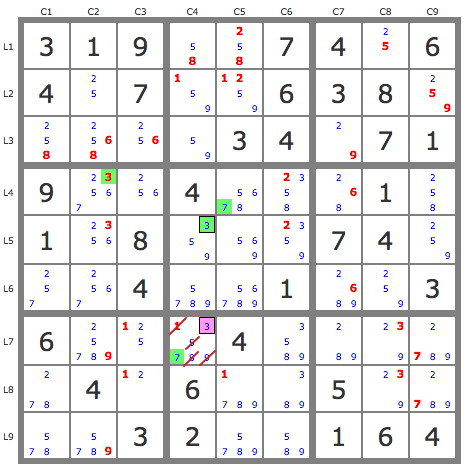
1. Y-Wing (5=29)b3p27 - (9=5)r3c4 => -5 r1c45
2. Extended Sue de Coq r4c56, r4c379, r1356c4 (RC 2568, 37 resp.)
=> -59 r2c4, -589 r7c4, -256 r4c2, -3 r5c6, -7 r6c5; 6 placements and basics
PM 9x9 (symmetric)

Hidden Text: Show

Code: Select all

5r4c5  6r4c5  7r4c5  8r4c5
5r4c6                8r4c6 2r4c6  3r4c6
5r4c3  6r4c3               2r4c3
       6r4c7         8r4c7 2r4c7
5r4c9                8r4c9 2r4c9
                                         5r1c4   8r1c4
                                         5r2c4          9r2c4
                                  3r5c4  5r5c4          9r5c4
              7r6c4                      5r6c4   8r6c4  9r6c4
---------------------------------------------------------------
-5r4c2 -6r4c2 -7r6c5       -2r4c2 -3r5c6 -5r27c4 -8r7c4 -9r27c4

Note: a simple AIC can be played instead of this SdC pattern. I like SdC

Hidden Text: Show

(7)r7c4 = r6c4 - r4c5 = (7-3)r4c2 = r4c6 - r5c4 = (3)r7c4 => -1 r7c4

Code: Select all

 +--------------------+----------------------+----------------------+
 |  3     1      9    |  8     2      7      |  4      5     6      |
 |  4    Z2-5*   7    |  1    z59     6      |  3      8    Z29*    |
 |  258   2568  Z56*  | y59    3      4      |  29     7     1      |
 +--------------------+----------------------+----------------------+
 |  9     37    Z56*  |  4     5678   2358   |  268    1   ZY258*   |
 |  1     2356   8    |  359   569    259    |  7      4     259    |
 | a257  A2567   4    | x579  W5689   1      | X2689   29    3      |
 +--------------------+----------------------+----------------------+
 |  6    c5789   1    |  37    4      3589   |  289    239   2789   |
 |  78    4      2    |  6     1      389    |  5      39    789    |
 | b578  c5789   3    |  2     5789   589    |  1      6     4      |
 +--------------------+----------------------+----------------------+

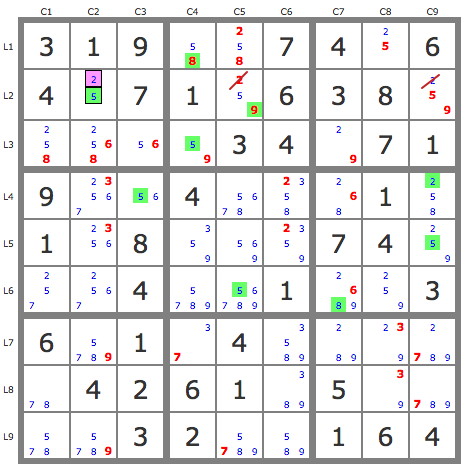
3. Kraken row (5)r6c1245 & almost S-wing (*)
(5)r6c1 - r9c1 = (5)r79c2
(5)r6c2
(5)r6c4 - r3c4 = (5)r2c5
(5-8)r6c5 = r6c7 - r4c9 = [(2)r2c2 = r2c9 - (2*=*5)r4c9 - r4c3 = (5)r3c3]
=> -5r2c2; ste

[DEFISE]

Here is my resolution with 3 whips of length <= 6

Hidden Text: Show

Single: 6r1c9
Single: 4r2c1
Single: 7r3c8
Single: 4r5c8
Single: 1r5c1
Single: 1r4c8
Single: 3r1c1
Single: 3r2c7
Alignment: 8-r1-b2 => -8r3c4
Alignment: 2-c6-b5 => -2r4c5 -2r5c5 -2r6c5
whip[4]: c4n3{r7 r5}- r4n3{c6 c2}- r4n7{c2 c5}- c4n7{r6 .} => -1r7c4
Single: 1r7c3
Single: 2r8c3
Single: 1r8c5
Single: 1r2c4
whip[3]: c5n2{r1 r2}- r2c2{n2 n5}- b3n5{r2c9 .} => -2r1c8
Single: 5r1c8
Single: 8r1c4
Single: 2r1c5
whip[6]: b2n5{r2c5 r3c4}- c3n5{r3 r4}- r6n5{c1 c5}- r6n8{c5 c7}- r4c9{n8 n2}- r2n2{c9 .} => -5r2c2

STTE

[Mauriès Robert]

Hi Cenoman,
Here is a two-step resolution, with TDP of course.

Step1 :
P'(3r7c4) : (-3r7c4) => 3r5c4->3r4c2->7r4c5->7r7c4->... => -1289r7c4 => r7c3=1 + 3 placements

puzzle1: Show

Step2

Code: Select all

                                         -------------->(8r1c4 & 9r2c5)->...
                                       /                     \                 
P'(2r2c2) : (-2r2c2) =>[ (5r2c2->5r3c4->5r4c3)->5r5c9]->5r6c5->8r6c7->2r4c9->...     
                                                  \                /
                                                    --------------   
                                 
=> -2r2c59 => r2c2=2, stte.


Diagram a little complicated but is very easy to understand with the markings on the puzzle.

puzzle2: Show

With the next pre-step, the second previous step is simplified and the resolution is in 3 steps.
P'(9L2C9) : (-9L2C9) => 9L3C7->5L3C4->5L2C2->... => -5L2C9 => L1C8=5 + 2 placements.

Robert

[denis_berthier]

After the trivial part:

Hidden Text: Show

hidden-single-in-a-row ==> r5c8 = 4
hidden-single-in-a-block ==> r4c8 = 1
hidden-single-in-a-block ==> r5c1 = 1
hidden-single-in-a-row ==> r3c8 = 7
hidden-single-in-a-row ==> r2c1 = 4
hidden-single-in-a-column ==> r1c1 = 3
hidden-single-in-a-block ==> r2c7 = 3
hidden-single-in-a-row ==> r1c9 = 6
168 candidates, 919 csp-links and 919 links. Density = 6.55%
whip[1]: c6n2{r5 .} ==> r6c5 ≠ 2, r4c5 ≠ 2, r5c5 ≠ 2
whip[1]: r1n8{c5 .} ==> r3c4 ≠ 8

reversible chains of max length 4 are enough:

Hidden Text: Show

finned-x-wing-in-columns: n7{c4 c1}{r6 r7} ==> r7c2 ≠ 7
biv-chain-rc[3]: r1c8{n5 n2} - r3c7{n2 n9} - r3c4{n9 n5} ==> r1c4 ≠ 5, r1c5 ≠ 5
singles ==> r1c4 = 8, r1c5 = 2, r1c8 = 5
biv-chain[3]: r4n7{c5 c2} - b4n3{r4c2 r5c2} - r5n6{c2 c5} ==> r4c5 ≠ 6
z-chain[3]: r2n2{c9 c2} - c1n2{r3 r6} - c8n2{r6 .} ==> r8c9 ≠ 2
biv-chain[4]: r4n3{c2 c6} - c4n3{r5 r7} - c4n7{r7 r6} - r4n7{c5 c2} ==> r4c2 ≠ 2, r4c2 ≠ 5, r4c2 ≠ 6
biv-chain[4]: r4n3{c6 c2} - r4n7{c2 c5} - c4n7{r6 r7} - c4n3{r7 r5} ==> r5c6 ≠ 3
biv-chain[4]: r4n7{c5 c2} - b4n3{r4c2 r5c2} - c4n3{r5 r7} - b8n1{r7c4 r8c5} ==> r8c5 ≠ 7
biv-chain[4]: b8n7{r9c5 r7c4} - c4n3{r7 r5} - r4n3{c6 c2} - r4n7{c2 c5} ==> r6c5 ≠ 7
biv-chain[4]: b8n7{r7c4 r9c5} - r4n7{c5 c2} - r4n3{c2 c6} - c4n3{r5 r7} ==> r7c4 ≠ 1, r7c4 ≠ 5, r7c4 ≠ 9
singles ==> r8c5 = 1, r8c3 = 2, r2c4 = 1, r7c3 = 1
finned-x-wing-in-columns: n5{c3 c4}{r3 r4} ==> r4c6 ≠ 5, r4c5 ≠ 5
finned-x-wing-in-rows: n5{r2 r7}{c2 c5} ==> r9c5 ≠ 5
whip[1]: b8n5{r9c6 .} ==> r5c6 ≠ 5
finned-x-wing-in-rows: n9{r2 r5}{c9 c5} ==> r6c5 ≠ 9
biv-chain[3]: b6n5{r5c9 r4c9} - c3n5{r4 r3} - b2n5{r3c4 r2c5} ==> r5c5 ≠ 5
biv-chain[3]: c5n5{r6 r2} - r2c2{n5 n2} - c1n2{r3 r6} ==> r6c1 ≠ 5
biv-chain[3]: r2n2{c9 c2} - c1n2{r3 r6} - c8n2{r6 r7} ==> r7c9 ≠ 2
biv-chain[3]: r3c7{n9 n2} - r7n2{c7 c8} - r6c8{n2 n9} ==> r6c7 ≠ 9
biv-chain[3]: b2n9{r2c5 r3c4} - c7n9{r3 r7} - b7n9{r7c2 r9c2} ==> r9c5 ≠ 9
whip[1]: b8n9{r9c6 .} ==> r5c6 ≠ 9
stte