What solution will you bring to this rather difficult puzzle?
Cordialy
Robert
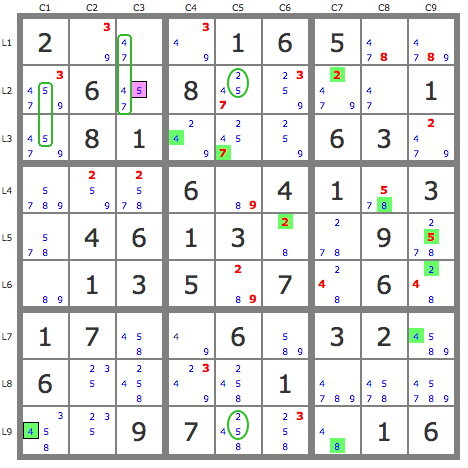
2....65.....8....1.81....3....6.41...4..3..9...35.7....7....32.6....1.....97....6
puzzle: Show
(solve "2....65.....8....1.81....3....6.41...4..3..9...35.7....7....32.6....1.....97....6")
***********************************************************************************************
*** SudoRules 20.1.s based on CSP-Rules 2.1.s, config = W+SFin
*** Using CLIPS 6.32-r774
***********************************************************************************************
singles ==> r9c8 = 1, r7c1 = 1, r6c2 = 1, r5c3 = 6, r2c2 = 6, r3c7 = 6, r6c8 = 6, r5c4 = 1, r1c5 = 1, r7c5 = 6, r4c9 = 3
165 candidates, 831 csp-links and 831 links. Density = 6.14%
whip[1]: b5n9{r6c5 .} ==> r8c5 ≠ 9, r2c5 ≠ 9, r3c5 ≠ 9
whip[1]: b4n2{r4c3 .} ==> r4c5 ≠ 2
x-wing-in-columns: n3{c1 c6}{r2 r9} ==> r9c2 ≠ 3
finned-x-wing-in-columns: n5{c8 c2}{r4 r8} ==> r8c3 ≠ 5
biv-chain[3]: c7n9{r8 r2} - b3n2{r2c7 r3c9} - c4n2{r3 r8} ==> r8c4 ≠ 9
whip[1]: r8n9{c9 .} ==> r7c9 ≠ 9
z-chain[3]: c1n3{r2 r9} - c1n4{r9 r3} - r1c3{n4 .} ==> r2c1 ≠ 7
z-chain[4]: b1n3{r2c1 r1c2} - b1n9{r1c2 r3c1} - c1n4{r3 r9} - c1n3{r9 .} ==> r2c1 ≠ 5
biv-chain[5]: r5c6{n2 n8} - r4c5{n8 n9} - c2n9{r4 r1} - c2n3{r1 r8} - b8n3{r8c4 r9c6} ==> r9c6 ≠ 2
t-whip[5]: r2n3{c1 c6} - c4n3{r1 r8} - c4n2{r8 r3} - r2n2{c6 c7} - r2n9{c7 .} ==> r2c1 ≠ 4
naked-pairs-in-a-block: b1{r1c2 r2c1}{n3 n9} ==> r3c1 ≠ 9
z-chain[5]: c1n4{r3 r9} - b7n3{r9c1 r8c2} - r1c2{n3 n9} - b3n9{r1c9 r2c7} - b3n2{r2c7 .} ==> r3c9 ≠ 4
t-whip[5]: b3n2{r2c7 r3c9} - c4n2{r3 r8} - r8n3{c4 c2} - r1c2{n3 n9} - b3n9{r1c9 .} ==> r2c7 ≠ 4, r2c7 ≠ 7
t-whip[6]: b8n3{r9c6 r8c4} - c4n2{r8 r3} - c6n2{r3 r5} - c9n2{r5 r6} - r6n4{c9 c7} - r9c7{n4 .} ==> r9c6 ≠ 8
biv-chain[3]: r8n3{c2 c4} - r9c6{n3 n5} - r9c2{n5 n2} ==> r8c2 ≠ 2
biv-chain[4]: c2n9{r1 r4} - r4c5{n9 n8} - c6n8{r5 r7} - b8n9{r7c6 r7c4} ==> r1c4 ≠ 9
t-whip-cn[5]: c3n2{r4 r8} - c4n2{r8 r3} - c6n2{r3 r5} - c6n8{r5 r7} - c3n8{r7 .} ==> r4c3 ≠ 5, r4c3 ≠ 7
whip[1]: b4n7{r5c1 .} ==> r3c1 ≠ 7
t-whip[4]: c3n5{r2 r7} - r8c2{n5 n3} - b8n3{r8c4 r9c6} - r9n5{c6 .} ==> r2c5 ≠ 5
t-whip[4]: c5n7{r3 r2} - r2c8{n7 n4} - r2c3{n4 n5} - r3c1{n5 .} ==> r3c5 ≠ 4
whip[5]: c8n5{r8 r4} - r5n5{c9 c1} - r3c1{n5 n4} - r2n4{c3 c5} - r9n4{c5 .} ==> r8c8 ≠ 4
whip[1]: c8n4{r2 .} ==> r1c9 ≠ 4
t-whip[6]: r3n7{c5 c9} - b3n2{r3c9 r2c7} - b3n9{r2c7 r1c9} - r1c2{n9 n3} - r8n3{c2 c4} - c4n2{r8 .} ==> r3c5 ≠ 2
t-whip[6]: r6n2{c9 c5} - r9n2{c5 c2} - r8n2{c3 c4} - r8n3{c4 c2} - c2n5{r8 r4} - b6n5{r4c8 .} ==> r5c9 ≠ 2
finned-x-wing-in-rows: n2{r5 r2}{c7 c6} ==> r3c6 ≠ 2
biv-chain[5]: r9c7{n8 n4} - r6n4{c7 c9} - c9n2{r6 r3} - r2c7{n2 n9} - r8n9{c7 c9} ==> r8c9 ≠ 8
z-chain[5]: r3n4{c4 c1} - b7n4{r9c1 r7c3} - c9n4{r7 r6} - c9n2{r6 r3} - c4n2{r3 .} ==> r8c4 ≠ 4
biv-chain-rc[3]: r8c4{n2 n3} - r9c6{n3 n5} - r9c2{n5 n2} ==> r9c5 ≠ 2, r8c3 ≠ 2
singles ==> r9c2 = 2, r4c3 = 2
whip[1]: c3n8{r8 .} ==> r9c1 ≠ 8
x-wing-in-columns: n5{c2 c8}{r4 r8} ==> r8c9 ≠ 5, r8c5 ≠ 5, r4c1 ≠ 5
biv-chain[2]: r9n8{c7 c5} - c6n8{r7 r5} ==> r5c7 ≠ 8
biv-chain[4]: r2c7{n9 n2} - r3n2{c9 c4} - r8c4{n2 n3} - b2n3{r1c4 r2c6} ==> r2c6 ≠ 9
whip[1]: b2n9{r3c6 .} ==> r3c9 ≠ 9
biv-chain[3]: r3c9{n7 n2} - r2c7{n2 n9} - r8n9{c7 c9} ==> r8c9 ≠ 7
biv-chain[4]: r1n8{c8 c9} - r1n9{c9 c2} - r4c2{n9 n5} - c8n5{r4 r8} ==> r8c8 ≠ 8
biv-chain[3]: c9n5{r5 r7} - r8c8{n5 n7} - c7n7{r8 r5} ==> r5c9 ≠ 7
whip[1]: c9n7{r3 .} ==> r1c8 ≠ 7, r2c8 ≠ 7
singles ==> r2c8 = 4, r1c8 = 8
whip[1]: c5n4{r9 .} ==> r7c4 ≠ 4
singles ==> r7c4 = 9, r3c6 = 9
biv-chain-rc[3]: r1c3{n4 n7} - r1c9{n7 n9} - r8c9{n9 n4} ==> r8c3 ≠ 4
naked-single ==> r8c3 = 8
biv-chain[3]: b2n5{r2c6 r3c5} - r3c1{n5 n4} - r3c4{n4 n2} ==> r2c6 ≠ 2
stteMauriès Robert wrote:...which should make it easy to understand how the track was constructed.[...]
P'(5r2c3) = {-5r2c3, 47r12c3, 25r2c5, 4r9c1, 8r9c7, 25r9c5, 2r5c6, 5r23c1, 5r5c9, 8r4c8,...}
denis_berthier wrote:Mauriès Robert wrote:...which should make it easy to understand how the track was constructed.[...]
P'(5r2c3) = {-5r2c3, 47r12c3, 25r2c5, 4r9c1, 8r9c7, 25r9c5, 2r5c6, 5r23c1, 5r5c9, 8r4c8,...}
Your track gives me no idea how to reach 4r9c1.
Mauriès Robert wrote:Hi Denis,denis_berthier wrote:Mauriès Robert wrote:...which should make it easy to understand how the track was constructed.[...]
P'(5r2c3) = {-5r2c3, 47r12c3, 25r2c5, 4r9c1, 8r9c7, 25r9c5, 2r5c6, 5r23c1, 5r5c9, 8r4c8,...}
Your track gives me no idea how to reach 4r9c1.
Here's how: -5r2c3->47r12c3->4r9c1
I wrote in the introduction the principle of building a track in general. It is therefore the last set in a chain of sets of candidates (or groups of candidates) obtained by applying the basic techniques (TB) from a starting hypothesis. It can be written like this for this anti-track whose starting hypothesis is -5r2c3 :
(-5r2c3)+TB=>{47r12c3}+TB=>{47r12c3, 25r2c5}+TB=>{-47r12c3, 25r2c5, 4r9c1}+TB=>{47r12c3, 25r2c5, 4r9c1, 8r9c7}... etc =>{47r12c3, 25r2c5, 4r9c1, 8r9c7, 25r9c5, 2r5c6, 5r23c1, 5r5c9, 8r4c8}
The order of the elements of the final set indicates how the set was constructed on the puzzle (colour marking).
This way of presentation is easier for me than making a graph showing all the implications.
Cordialy
Robert
denis_berthier wrote:Sorry, but this makes it still more obscure as to how 4r9c1 is deduced from the previous steps. Or do you mean it is NOT deduced from the previous steps?
Mauriès Robert wrote:Hi,denis_berthier wrote:Sorry, but this makes it still more obscure as to how 4r9c1 is deduced from the previous steps. Or do you mean it is NOT deduced from the previous steps?
It's hard to explain the simple things!
I build this anti-track step by step starting from the elimination (hypothesis) of the 5r2c3. This highlights the 47r12c3 doublet, so on the one hand that the 47r2c38 doublet indicates that 25r2c5 is part of the anti-track, but also that 4r1c9 is part of the anti-track.
Don't forget that I reason like a sudokist who does pencil marking, so you have to work on the puzzle physically!
Robert
denis_berthier wrote:I have no problem with the start: P'(5r2c3) = {-5r2c3, 47r12c3,
The problem is just after: I can see no way 4r9c1 can be deduced by "TB" from the preceding steps.
Obviously, some steps are missing before n4r9c1 can be highlighted.
Mauriès Robert wrote:Don't forget that I reason like a sudokist who does pencil marking, so you have to work on the puzzle physically!
SpAce wrote:denis_berthier wrote:I have no problem with the start: P'(5r2c3) = {-5r2c3, 47r12c3,
The problem is just after: I can see no way 4r9c1 can be deduced by "TB" from the preceding steps.
Obviously, some steps are missing before n4r9c1 can be highlighted.
What? I'm no fan of incomplete information, but I don't see any problem with that step. Two trivial routes:
(47)r12c3 - (4)r78c3 = (4)r9c1
denis_berthier wrote:OK, thanks; I was expecting something more complicated and I failed to see that.
That's the problem when the CSP-Variables one must check are not stated in the path.
matrices fail to capture the essential characteristics of chains. AND they can't be drawn on the grid.
SpAce wrote:For that reason I would recommend you reconsidered this earlier comment of yours:matrices fail to capture the essential characteristics of chains. AND they can't be drawn on the grid.
SpAce wrote:I don't think any other notation makes all that possible. That said, matrices obviously take a lot of space. That's where your notation has an edge. In fact, I've started to think that your notation might work as a compressed matrix, because they have such a direct mapping. From that point of view I can accept the missing z- and t-candidates, because they can be filled in from the grid if one needs to work with the complete matrix.
SpAce wrote:The biggest remaining problem I have with your notation is the quantum-leaping links in braids. I wish you marked them differently ('--' for example). That would be a quick fix that would remove a lot of confusion by making it clear that the link is not between adjacent nodes. That way the difference between whips and braids would also be visible in the chain itself and not just in the label, just like it is in the matrix where the gaps are obvious.
denis_berthier wrote:I think I understand the matrix notation pretty well. ... I don't see any new reason for revising my view about them
people have different ways of understanding the same things.
Of course, matrices themselves don't define any pattern. As you said, they can represent different types of patterns.
Modifying SudoRules to allow it to make a difference between a link to the previous candidate and a link to a more distant one is much more difficult than you think and it would entail a lot of inefficiencies.
I could put "--" systematically for all the links of all the braids, but that wouldn't help much more than warning it's a braid (and has to be read as such)
Anyway, you probably rarely see braids (let alone g-braids) in my resolution paths.
I consider braids essentially as a fundamental theoretical tool (relationship with T&E, confluence property, ...) - but the most useful pattern in practice is the whip.
And the totally unexpected miracle I fell upon (and that's totally independent of any notational system) is that their resolution powers are very close in spite of their very different computational complexities.
SpAce wrote:Anyway, you probably rarely see braids (let alone g-braids) in my resolution paths.
I understand. That said, it would be nice to see a bit of variety and more advanced patterns (and their notations). Maybe not braids, but perhaps some advanced whips
SpAce wrote:And the totally unexpected miracle I fell upon (and that's totally independent of any notational system) is that their resolution powers are very close in spite of their very different computational complexities.
For me a second miracle is that they have very different computational complexities, and to the whip's advantage. Why exactly is that?
SpAce wrote:For me it would seem logical that you'd get many more dead-ends if you only looked for whips, because it's the more specific type.