The New Sudoku Players' Forum

[Mauriès Robert]

Hi all,
Here's a new puzzle I suggest you solve, a rather difficult one.
For those who are interested, I give below an analysis of the puzzle, to see where to ignore before solving it!
Robert

.2...13..5.87.3.2.3.......5...43.....4.872.6.....16...6..1....7.5.6.79.4..73...8.

puzzle: Show

analysis: Show

Grid analysis
Grid analysis
Number of cells to solve = 50
Number of candidates to be resolved = 173
Number of back doors = 3
Number of uncertain generator candidates (dead-end runway) = 123
Number of invalid generator candidates = 47
Back doors are marked in blue, invalid generators in purple and uncertain generators in yellow.

[Cenoman]

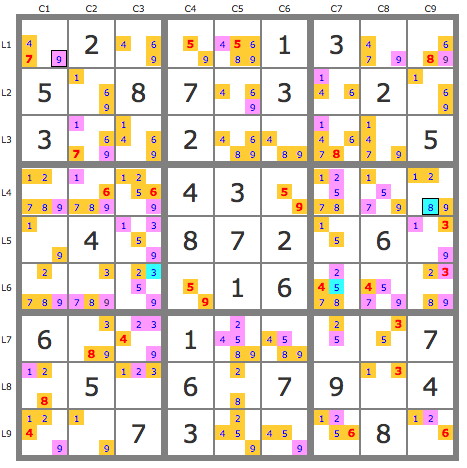
In seven steps:

Code: Select all

 +--------------------------+----------------------+------------------------+
 |  47-9    2       469     |  59   5689-4  1      |  3       79-4   689    |
 |  5       169     8       |  7    469     3      |  146     2      169    |
 |  3       1679    1469    |  2    4689    489    |  14678   1479   5      |
 +--------------------------+----------------------+------------------------+
 |  12789   16789   12569   |  4    3       59     |  12578   1579   1289   |
 |  19      4       1359    |  8    7       2      |  15      6      139    |
 |  278-9   3789    2359    |  59   1       6      |  24578   4579   2389   |
 +--------------------------+----------------------+------------------------+
 |  6       389     2349    |  1    24589   4589   |  25      35     7      |
 |  128     5       123     |  6    28      7      |  9       13     4      |
 |  124-    19      7       |  3    2459    459    |  1256    8      126    |
 +--------------------------+----------------------+------------------------+

1. (9=1)r9c2 - r8c13 = (1-35)r78c8 = r79c7 - (5=19)r5c17 => -9 r9c1

2. Kraken cell (459)r9c6
(4)r9c6 - r9c1 = (4)r1c1
(5)r9c6 - r4c6 = r6c4 - (5=9)r1c4
(9)r9c6 - (9=1)r9c2 - r8c13 = (1-35)r78c8 = r79c7 - (5=19)r5c17
=> -9 r1c1

3. Kraken cell (459)r9c6
(4)r9c6 - r9c1 = (4)r1c1
(5)r9c6 - r79c5 = (5*-86)r1c59 = r1c3 - (6=197)r239c2 - r1c1 = (7)r1c8
(9)r9c6 - (9=1)r9c2 - r23c2 = (1-4)r3c3 = (4)r1c13
=> -4 r1c5*, r1c8

4. Kraken row (9)r2c259
(9)r2c2 - (9=1)r9c2 - r8c13 = (1-35)r78c8 = r79c7 - (5=19)r5c17
(9)r2c5 - r1c4 = (9)r6c4
(9)r2c9 - r5c9 = (9)r5c13
=> -9 r6c1

Code: Select all

 +------------------------+----------------------+------------------------+
 |  47      2      469    |  5-9  5689    1      |  3       79*    689    |
 |  5       169    8      |  7    469     3      |  146     2      169    |
 |  3       1679   169    |  2    4689    489    |  14678   1479#  5      |
 +------------------------+----------------------+------------------------+
 |  12789   1678   1256   |  4    3       59     |  12578   1579*  1289   |
 |  19      4      135    |  8    7       2      |  15      6      139    |
 |  278     378    235    |  59*  1       6      |  24578   457-9  2389*  |
 +------------------------+----------------------+------------------------+
 |  6       389    2349   |  1    24589   4589   |  25      35     7      |
 |  128     5      123    |  6    28      7      |  9       13     4      |
 |  124     19     7      |  3    2459    459    |  1256    8      126    |
 +------------------------+----------------------+------------------------+

5. Kraken row (1)r3c2378
(1-7)r3c2 = r1c1 - (7=9)r1c8
(1-9)r3c3 = (94)r17c3 - (6=479)r1c138 - r1c4 = (9)r6c4
(1)r3c7 - (1=2564)r2579 - r3c8=(4)r6c8
(1-4)r3c8 = (4)r6c8
=> -9 r6c8

6. Almost kite [(9)r6c4=r6c9-r4c8=r1c8] = (9)r3c8-r3c3=(9-46)r17c3=(658)r1c459 => -9 r1c4; three placements & basics

Code: Select all

 +------------------------+---------------------+------------------------+
 |  47      2      469    |  5    689     1     |  3       79     689    |
 |  5       169    8      |  7    469     3     |  146     2      169    |
 |  3       1679   169    |  2    4689    489   |  14678   1479   5      |
 +------------------------+---------------------+------------------------+
 |  12789   1678   126    |  4    3       5     |  1278    179    1289   |
 |  19      4      135    |  8    7       2     |  15      6      139    |
 |  278     378    235    |  9    1       6     |  24578   47-5   238    |
 +------------------------+---------------------+------------------------+
 |  6       389    2349   |  1    24589   489   |  25      35     7      |
 |  128     5      123    |  6    28      7     |  9       13     4      |
 |  124     19     7      |  3    2459    49    |  1256    8      126    |
 +------------------------+---------------------+------------------------+

7. Multi-krakens (9)r2c259 & (7)r346c2 & (1)r2459c9 (as a net)

Code: Select all

                                                 (7-3)r6c2 = r7c2 - (3=5)r7c8 *
                                                  ||
                                                 (7)r4c2 - r4c78 = (74)r6c78 *
                                                  ||
(9)r2c2 - r79c2 = (9-4)r7c3 = r9c1 - (4=7)r1c1 - (7)r3c2
 ||
(9-4)r2c5 = r2c7 - r6c7 = (4)r6c8 *
 ||
(9-1)r2c9
   ||
  (1)r45c9 - (1=5)r5c7 *
   ||
  (1)r9c9 - (1=35)r78c8 *
---------------
=> -5 r6c8; ste