The New Sudoku Players' Forum

by **Mauriès Robert** » Wed Jan 15, 2020 3:22 pm

Hi,
I offer you this rather difficult puzzle that requires several steps.
Who will make the best resolution ?
..6...98.....8.5.....9.6.471...34..5.........2..75...889.2.1.5...1.4.....52...8..

Code: Select all: +-------+-------+-------+ | . . 6 | . . . | 9 8 . | | . . . | . 8 . | 5 . . | | . . . | 9 . 6 | . 4 7 | +-------+-------+-------+ | 1 . . | . 3 4 | . . 5 | | . . . | . . . | . . . | | 2 . . | 7 5 . | . . 8 | +-------+-------+-------+ | 8 9 . | 2 . 1 | . 5 . | | . . 1 | . 4 . | . . . | | . 5 2 | . . . | 8 . . | +-------+-------+-------+

Robert

by **Ngisa** » Wed Jan 15, 2020 4:57 pm

It will be better if you can provide a printable version like Tarek.

by **Mauriès Robert** » Wed Jan 15, 2020 5:31 pm

Hi Clément,
There, I added the puzzle to my post.
Robert

by **totuan** » Sat Jan 18, 2020 4:32 pm

Mauriès Robert wrote:Who will make the best resolution ?

Maybe, it’s not me

After basic SSTS:

Code: Select all: *-----------------------------------------------------------------------------* | 347 12347 6 | 1345 127 2357 | 9 8 123 | | 3479 12347 3479 | 134 8 237 | 5 1236 1236 | | 35 1238 358 | 9 12 6 | 123 4 7 | |-------------------------+-------------------------+-------------------------| | 1 678 789 | 68 3 4 | 267 2679 5 | | 345679 34678 345789 | 168 126 28 | 3467 3679 3469 | | 2 346 34 | 7 5 9 | 1346 136 8 | |-------------------------+-------------------------+-------------------------| | 8 9 347 | 2 67 1 | 3467 5 346 | | 367 367 1 | 58 4 58 | 2367 23679 2369 | | 467 5 2 | 36 9 37 | 8 167 146 | *-----------------------------------------------------------------------------*

Nearly TET holiday (Lunar New Year – Mouse Year) in Vietnam with many Year End Party - the time for wine & vodka, then not much time for Sudoku

On considering DP (3479)r267c3, I have found that cell (347)r7c3 as key to eliminate r2c6<>7. But to limit to Triple Krakens it’s required more two step.
My path for this one – not nice path

01- Present as diagram: => r7c9<>6

Code: Select all: (XY-wing:(467)r7c35/r9c1)-(6)r9c4=r7c5* || || AALS(3479)r12c1/r2c3 || || || -(4)r7c3=r9c1-(4)r12c1 || | || (3)r7c3--(3=4)r6c3----(4)r2c3 AALS(12346)r129c9 || | || || || | (379)r12c1/r2c3-(3)r3c123=r3c7-(3)r12c9 || | || || -(4)r7c3=r9c1--------------------------------(4)r9c9 || || || (6)r6c8-r2c8=r2c9* (126)r129c9* || || (7)r9c1--(4)r9c1=r7c3-(4=3)r6c3-(3)r6c8 | || -(4)r9c1=(4-1)r9c9=r9c8-(1)r6c8

02- Present as diagram: => r5c89<>6

Code: Select all: (6)r9c4-r7c5=r5c5* (6)r6c8* || || (6)r9c1--(4)r9c1=r7c3-(4=3)r6c3-(3)r6c8 || | || || -(4)r9c1=(4-1)r9c9=r9c8-(1)r6c8 || (X-wing:6’s r29c89)*

03- Present as diagram: => r2c6, r1c12<>7

Code: Select all: (7)r7c3-r7c5=r1c5* || AAHS(3479)r2c13 || || || -(4)r7c3=r9c1----------------------------(4)r2c1 || | || (3)r7c3--(3=4)r6c3-------------------------------(4)r2c3 || | || || | (79)r2c13* || | || || | (3)r8c7-r3c7=r3c123---------(3)r2c13 || | || || -(3=67)r8c12-(67)r8c7 (7)r2c3* || | || || || | (2)r8c7-r4c7=(2-9)r4c8=r4c3-(9)r2c3 || | || || -(3=34)r67c3-----------------------------(34)r2c3 || (4)r7c3--(4=3)r7c9----(3)r5c9 | || -(4)r9c1=r9c9-(4)r5c9 (7)r2c3* | || || | (9)r5c9-r4c9=r4c3----------(9)r2c3 | || -(4=34)r67c3-----------------------------(34)r2c3

04- (2)r5c5=r5c6-(2=3)r2c6-(3=7)r9c6-(7=6)r7c5 => r5c5<>6, some singles.
05- (3)r3c7=r3c123-(3=4)r1c1-r9c1=(4-1)r9c9=r9c9-r6c8=r6c7 => r3c7<>1, r6c7=1
06- (4)r5c7=(4-9)r5c9=(9-2)r8c9=r12c9-(2=3)r3c7 => r5c7<>3
07- (3=4)r7c9- r7c3=r9c1-(4=3)r1c1-(358=12)r3c1235-(2=3)r3c7 => r12c9, r78c7<>3, some singles.
08- (3=4)r6c3-r7c3=r9c1-(4=3)r1c1 => r2c3, r5c1<>3
09- (6=3)r6c8-r6c3=r7c3-(3=4)r7c9-r5c9=r5c7 => r5c7<>6
10- Colors 6’s: r6c3=r6c8-r4c7=r8c7 => r8c2<>6, stte.

Have a nice weekend to All!
totuan

by **Mauriès Robert** » Sun Jan 19, 2020 6:13 pm

Hi Totuan,
First of all thank you for taking the time to solve this puzzle and presenting your solution in a very detailed way.
This puzzle can be solved quickly if you agree to look for the contradiction, like this:
P(6r6c4) : 6r6c4 -> contradiction => -6r6c4, then P(4r9c1) : 4r9c1 -> contradiction => -4r9c1, stte.
But on this forum this is not accepted, so here is my 7-step resolution (which could be reduced to 6 steps)

Step1 :
P'(1r6c7) : -1r6c7 -> --- ->4r6c3 (see diagram and puzzle1) => -4r6c7 => -4r5c123

Code: Select all: ----------------------- | | -1r6c7->1r6c8->1r9c9->4r9c1->7r1c1->7r3c6->7r7c5->3r7c3->4r6c3 | | ->1r3c7->2r3c5->358r3c123

puzzle1: Show

Step2 :
P'(3r6c23) : -3r6c23-> --- (see diagram and puzzle2) => -3r3c123 => 34r6c23, 16r6c78, -6r45b6

Code: Select all: and(*)->6r5c7->4r5c9->3r7c9and(*)->3r8c2 | | | ------------- | | |->8r4c2and(*)->6r4c4->6r7c5->7r9c6| |->7r4c2and(*)->3r8c2->7r7c3->7r9c6|->7r1c5and(*)->3r1c1->5r3c1->5r5c3 | P'(3r6c23) : [-3r6c23->(4r6c3->4r9c1)->6r6c2->6r8c1](*) | | | ------------------

puzzle2: Show

Step3 :
P'(2r3c5) : -2r3c5->1r3c5-> --- ->2r4c7 (see diagram and puzzle3) => -2r3c7

Code: Select all: ------------------------------- | | ->7r9c6->3r9c4and(*)->6r9c1->37r8c12->7r7c7->2r4c7 | [-2r3c5->1r3c5->1r6c7->6r6c8->6r2c9](*)-> | ->3r9c6->-------------- | | | ->7r7c5->6r9c4->6r5c5->2r5c6->7r2c6 | | | ------------------ | | ->34r7c3->9r2c3->9r4c8->2r4c7

puzzle3: Show

Step4 :
P(1r3c7) and P(3r3c7) (see diagram and puzzle 4) => r3c1=5, r3c3=8, r5c3=5, -1r2c9, -6r9c89

Code: Select all: ->6r9c4->8r4c4---------------->8r3c3 | | ->1r6c8->1r9c9->4r9c1->7r1c1->(7r2c6->7r7c5->34r67c4)->9r2c3->9r5c1->5r5c3->5r5c1 | | [1r3c7->2r3c5]->358r3c123-- And [3r3c7->5r3c1->5r5c3]->8r3c3 | ->1r6c7->6r6c8->6r2c9

puzzle4: Show

Step5 :
P(4r9c9) and P(4r9c1) (see diagram and puzzle5) => r3c7=3 and 3 placements.

Code: Select all: 4r9c9->1r9c8->1r6c7->3r3c7 and 4r9c1->1r9c9->7r9c8->7r7c5->3r7c3->3r6c2->3r3c7 | | -----------------------

puzzle5: Show

Step6 :
P(4r9c9) and P(4r9c1) (see diagram and puzzle6) => r5c7=4, r4c3=9, r2c3=7

Code: Select all: (4r9c9->3r7c9)->(9r5c9->9r4c3)->4r5c7 | | ->4r7c3->3r6c3-------->7r2c3 and -------------------------- | | 4r9c1->1r9c9->7r9c8->7r7c5->6r7c7->4r5c7 | | | | ---------------------->7r4c7->9r4c3->7r2c3

puzzle6: Show

Step7 :
P'(7r1c5) : -7r1c5->12r13c5->2r5c6->8r8c6->5r1c6 => -7r1c6, stte

Robert

by **Cenoman** » Sun Jan 19, 2020 9:13 pm

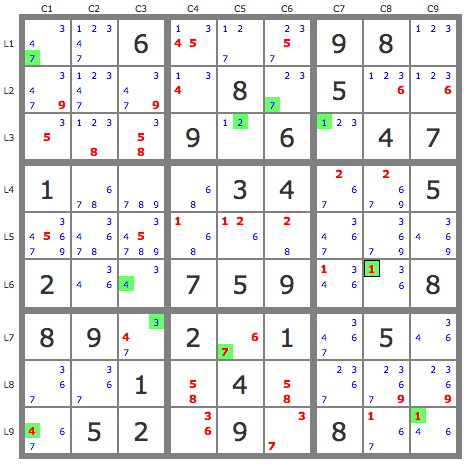
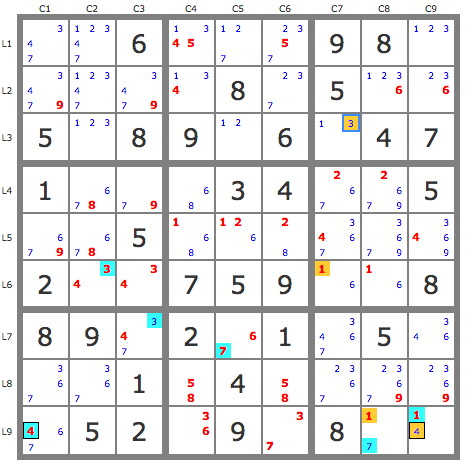
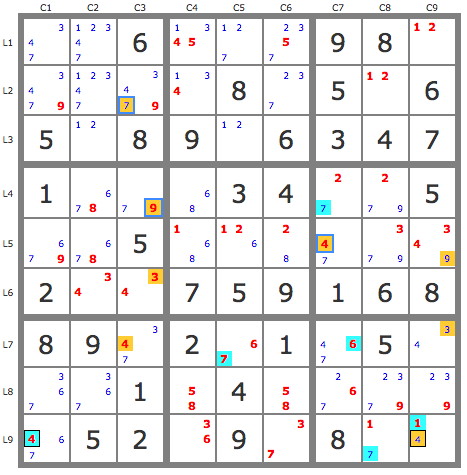
Solution in eight steps, out of which two are complex (multikrakens)

Code: Select all: +----------------------------+----------------------+------------------------+ | 347 12347 6 | 1345 127 2357 | 9 8 123 | | 3479 12347 3479 | 134 8 237 | 5 1236 1236 | | 35 1238 358 | 9 12 6 | 123 4 7 | +----------------------------+----------------------+------------------------+ | 1 678 789 | 68 3 4 | 267 2679 5 | | 345679 34678 345789 | 168 126 28 | 3467 3679 3469 | | 2 346 34 | 7 5 9 | 1346 136 8 | +----------------------------+----------------------+------------------------+ | 8 9 347 | 2 67 1 | 3467 5 346 | | 367 367 1 | 58 4 58 | 2367 23679 2369 | | 467 5 2 | 36 9 37 | 8 167 146 | +----------------------------+----------------------+------------------------+

1. (7=3)r9c6 - (3=127)b2p268 => -7 r1c6

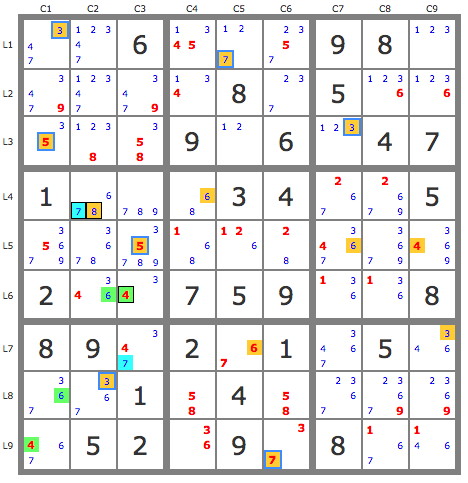
2. Kraken row (7)r2c1236
(79)r2c13
(7)r2c2 - (7=3684)r4568c2- (4=3)r6c3
(7)r2c6 - r1c5 = r7c5 - (7=43)r7c3
=> -3 r2c3

3. (3=4)r6c3 - r56c2 = r12c2 - (4=793*5)b1p1467 - r3c3 = (5)r5c3 => -3 r3c3*, r5c3
4. (4)r6c23 = (4-1)r6c7 = (1-3)r3c7 = r3c12 - (3=794)b1p146 - r12c2 = (4)r56c2 => -4 r5c13

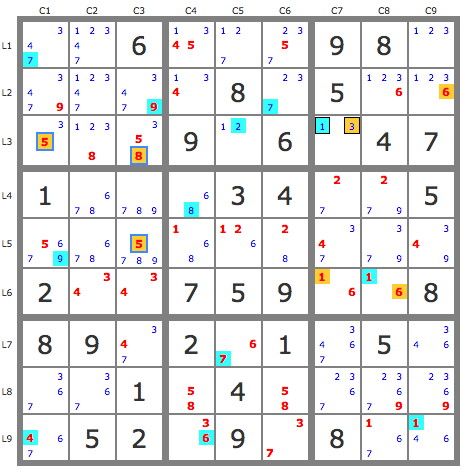
5. Double kraken, cell (347)r7c3 & row (7)r2c1236
(3)r7c3 - (3=4)r6c3 - r56c2 = r12c2 - (4=793)b1p146 - r3c12 = (3)r3c7
(4)r7c3 - (4=3671)r9c1468 - r6c8 = (1)r6c7
(7)r7c3 - [(7)r7c5 = r1c5 - r2c6 = (79)r2c13 - (4)r2c3 = (34)r67c3] = (7)r2c2 - (7=493)b1p146 - r3c12 = (3)r3c7
=> -1 r3c7; one placement
Same as a net

Hidden Text: Show

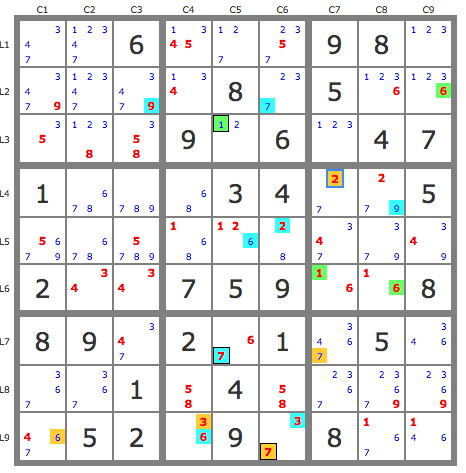
6. Quadruple kraken, cell (267)r4c7 & cell (368)r8c2 & almoste kite (7)r7c6 & cell (479)r2c3
(2)r4c7 - r8c7 = (29)r8c89
(6)r4c7 - [(6)r6c78 = r6c2 - (6=7)r8c2 - (7=86)r4c24] = (3)r8c2
(7)r4c7 - r7c7 = [(7)r7c3 = r7c5 - r9c6 = r2c6] - (7)r2c3
||(4)r2c3 - (4=3)r6c3 - r7c3 = (3)r8c12
||(9)r2c3 - (9=6782)r4c2347 - r8c7 = (29)r8c89
=> -3 r8c89
Same as a net:

Hidden Text: Show

Code: Select all: +--------------------------+---------------------+-----------------------+ | 347 12347 6 | 1345 127 235 | 9 8 123 | | 3479 12347 479 | 134 8 237 | 5 1236 1236 | | 35 1238 58 | 9 12 6 | 23 4 7 | +--------------------------+---------------------+-----------------------+ | 1 678 789 | 68 3 4 | 267 2679 5 | | 35679 3678 5789 | 168 126 28 | 3467 3679 3469 | | 2 346 34 | 7 5 9 | 1 36 8 | +--------------------------+---------------------+-----------------------+ | 8 9 347 | 2 67 1 | 3467 5 346 | | 367 367 1 | 58 4 58 | 2367 2679 269 | | 467 5 2 | 36 9 37 | 8 167 146 | +--------------------------+---------------------+-----------------------+

7. (3=4)r6c3 - r6c2 = r12c2 - (4=793)b1p146 - r3c12 = r3c7 - r8c7 = (3)r8c12 => -3 r7c3; four placements

Code: Select all: +-----------------------+---------------------+---------------------+ | 347 1237 6 | 1345 127 235 | 9 8 123 | | 3479 1237 479 | 134 8 237 | 5 123 6 | | 35 1238 58 | 9 12 6 | 23 4 7 | +-----------------------+---------------------+---------------------+ | 1 678 789 | 68 3 4 | 27 279 5 | | 5679 678 5789 | 168 126 28 | 347 379 349 | | 2 4 3 | 7 5 9 | 1 6 8 | +-----------------------+---------------------+---------------------+ | 8 9 47 | 2 67 1 | 3467 5 34 | | 367 367 1 | 58 4 58 | 267 279 29 | | 467 5 2 | 36 9 37 | 8 17 14 | +-----------------------+---------------------+---------------------+

8. (7)r9c6 = r7c5 - (7=4)r7c3 - r9c1 = (4-1)r9c9 = (1)r8c8 => -7 r9c8; ste

The New Sudoku Players' Forum

Robert's puzzles 2020-01-15

Robert's puzzles 2020-01-15

Re: Robert's puzzles 2020-01-15

Re: Robert's puzzles 2020-01-15

Re: Robert's puzzles 2020-01-15

Re: Robert's puzzles 2020-01-15

Re: Robert's puzzles 2020-01-15