The New Sudoku Players' Forum

[Mauriès Robert]

Hi,
Here is the last puzzle I propose to you in 2019 and I'll see you in 2020 for the next one.
Its level of difficulty is established at 11266 by Hodoku.

...6.3.....3.9.1......4.....7.916.2..........4.9...7.8.2..6..1.7..5.1..38.......7

puzzle: Show

Robert

[totuan]

Hi ALL,

Code: Select all

 *--------------------------------------------------------------------*
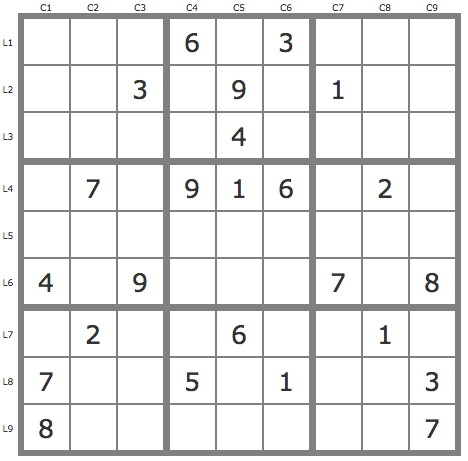
 | 1      4589   2457   | 6      2578   3      | 4589   45789  2459   |
 | 256    4568   3      | 278    9      2578   | 1      4578   2456   |
 | 2569   5689   2567   | 1      4      2578   | 3589   35789  2569   |
 |----------------------+----------------------+----------------------|
 | 35     7      8      | 9      1      6      | 345    2      45     |
 | 2356   356    256    | 478    78     478    | 359    359    1      |
 | 4      1      9      | 23     235    25     | 7      6      8      |
 |----------------------+----------------------+----------------------|
 | 359    2      45     | 3478   6      4789   | 4589   1      459    |
 | 7      469    46     | 5      28     1      | 26     489    3      |
 | 8      34569  1      | 234    23     249    | 26     459    7      |
 *--------------------------------------------------------------------*

My path for this one. Again, it’s required Triple Kraken to downgrade for the puzzle with ER 9.0 .
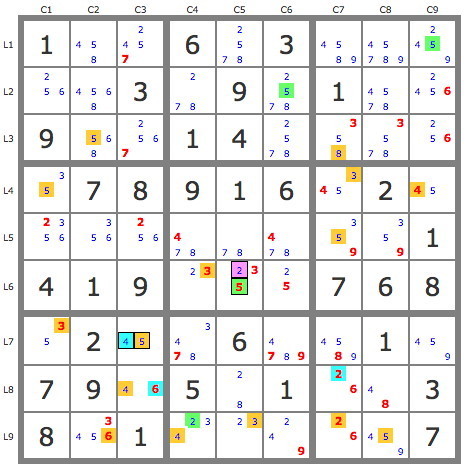
Look at: if r2c4<>2 => XY chain:(2)r9c4=(2-3)r6c4=r6c5-(3=2)r9c5 => r8c5<>2

01- (9)r3c1-r7c1-r7c9=r13c9 => r3c78<>9
02- Present as diagram: => r8c5<>2, some singles.

Code: Select all

(2)r2c9---------(2)r2c4=[(2)r9c4=(2-3)r6c4=r6c5-(3=2)r9c5]*
 ||              |
(6)r2c9-(6)r2c1  |
 ||      ||      |
 ||     (2)r2c1--
 ||      ||
 ||     (5)r2c1-(5=3)r4c1----------------------(3)r7c1=r9c2-(3=2)r9c5*
 ||                                             |
(4)r2c9-(4=5)r4c9-(5=3)r4c1---------------------|
 ||                                             |
 ||      ---------------------(5)r3c7           |
 ||     |                      ||               |
 ||     |             (8)r3c2-(8)r3c7           |
 ||     |              ||      ||               |
 ||     |              ||     (3)r3c7-r4c7=r4c1-|
 ||     |              ||                       |
(5)r2c9--(6)r2c9=r3c9-(6)r3c2                   |
        |              ||                       |
        |             (9)r3c2-r3c1=(9)r7c1------
        |              ||   
        |             (5)r3c2-(5)r1c23 
        |                      ||
        |                     (5)r1c5-(78=8)r158c5*
        |                      ||
         ---------------------(5)r1c789

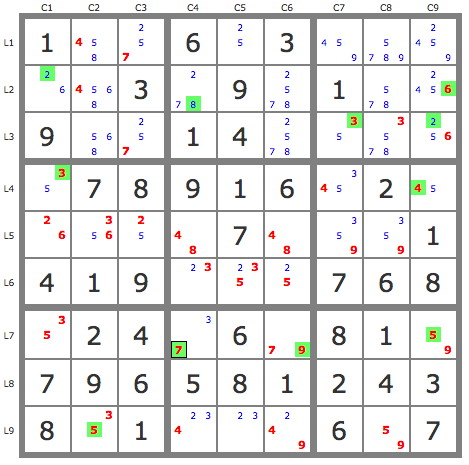
03- (5=3)r3c7- r4c7=r4c1-r7c1=r9c2-(3=2)r9c5-(2=5)r1c5 => r1c789<>5
04- (4)r4c9-r4c7=(4-9)r1c7-r5c7=r5c8-(9=4)r8c8 => r7c9<>4
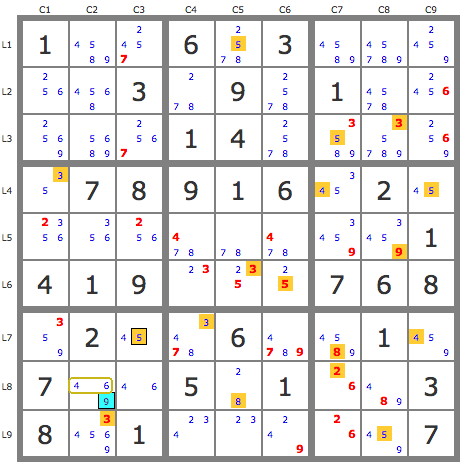
05- XY-wing: (459)r7c39/r8c8 => r8c23<>4, some singles.
06- Present as diagram – Kraken Cell (257)r3c3: => r2c8<>7

Code: Select all

(7)r3c3-r3c6=r2c46*
 ||
(2)r3c3-(2=5)r5c3-(5=3)r4c1--r7c1=(3-7)r7c4=r2c4*
 ||                         |
(5)r3c3-(5=3)r3c7-r4c7=r4c1-

07- (2)r2c1=r5c1-(2=5)r5c3-r4c1=(5-3)r7c1=(3-7)r7c4=r2c4 => r2c4<>2
08- (5=3)r3c7-r3c8=r5c8-r5c2=(3-5)r9c2=r9c8 => r2c8<>5, some singles.
09- XYZ-wing: (345)r4c79/r3c7 => r5c7<>5, stte

Ps: thanks to SpAce for explaining on December 29-2019 puzzle

HAPPY NEW YEAR 2020 to ALL!!!

totuan

[Mauriès Robert]

Hi,
Congratulations Totuan for your tenacity and your interest in my puzzles. The grids of this level are not easy to solve if you don't accept to use the chain (track) of direct contradiction.
Here is my 3-step resolution with TDP :
1) With an anti-track:
P'(9r8c2) : -9r8c2-> ---- ->9r5c8 (see diagram and puzzle1) =>-9r8c8 => r8c2=9 and r3c1=9

Code: Select all

                                                 ->5r3c7->3r3c8->9r5c8
                                                |
 -9r8c2->46r8c23->5r7c3->5r9c8----------------->|<----------------------------------------
             \                                  |                                         |
              ->(2r8c7->8r8c5->8r7c7)->4r7c9->5r4c9->3r4c1->3r9c2->3r7c4->3r6c5->5r6c6->5r1c5


puzzle1: Show

2) With two conjugated tracks and an extension :
P(4r7c3) : 4r7c3->6r8c3->2r8c7->8r8c5
P(5r7c3) : 5r7c3-> --- ->8r8c5 (see diagrame and puzzle2)
=> r8c5=8,-4r9c2 =>+7 placements

Code: Select all

                                       ->2r6c5->8r8c5
                                      /
                   ->2r9c7->3r9c5->3r6c4----------------------------------------
                 /                    \                                         \
                /                      ->5r6c5--------                           \
               /                                      \                           \
    ->4r8c3->6r9c2----------------------------->5r3c2--->5r2c6->5r1c9->*26r2c19->2r9c4->8r8c5
  /                                          /                /
5r7c3->3r7c1->(5r4c1->4r4c9*)->3r4c7------>8r3c7             /
  \                      \       \      /                   /
   ->5r9c8------------------------->5r5c7-------------------


puzzle2: Show

3) With an anti-track:
P'(3r7c4) : -3r7c4-> --- ->3r4c1 (see diagram and puzzle3) => -3r7c1, stte.

Code: Select all

                           -------------------->2r3c9
                          /                  /    \
                         /--------------->6r2c9    \
                        /       /                   \
-3r7c4->7r7c4->9r7c6->5r7c9->4r4c9                   \
           \            \                             \
            \             ->5r9c2->57r13c3->2r2c1      \
             \                                 \        \
               ---------------------------------->8r3c4--->57r3c36->3r3c7->3r4c1


puzzle3: Show

Ouf!
Robert