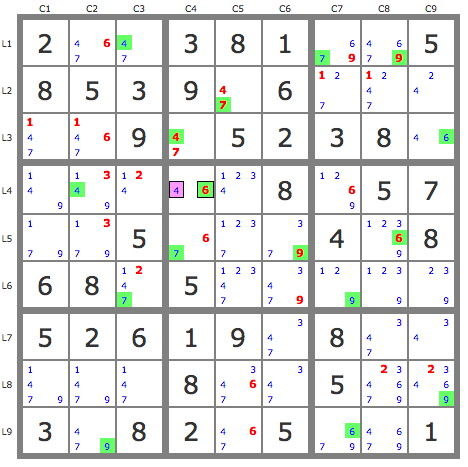
Here's my christmas grid
I'm interested in your solving this puzzle, what will it be ?
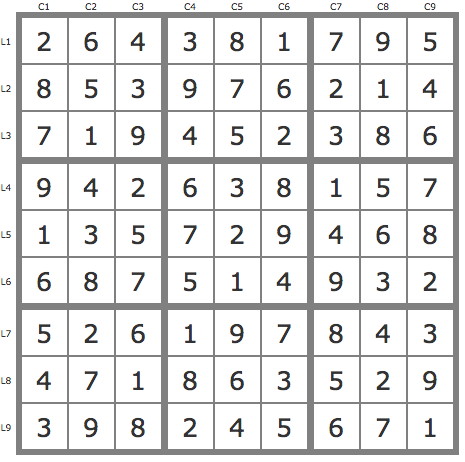
2....1..5..3..6.....9.5.38......8.57..5...4..68........26.9.8.....8..5..3..2....1
Sincerely
Robert
my resolution with TDP: Show
After reduction of the grid by the basic techniques, the solution can be found quickly by tracing on the grid the conjugate tracks P(2r2c5) and P(2r3c6) which places the 2r3c6, then P(6r4c4) and P(6r5c4), one of which is invalid and the other gives the solution. But here is another step-by-step resolution that does not use direct contradiction.
1) P'(2r3c6) : -2r3c6->2r3c9->6r8c9->[9r6c9->9r5c6, 2r8c8]->2r5c5 => -2r2c5 => r3c6=2.
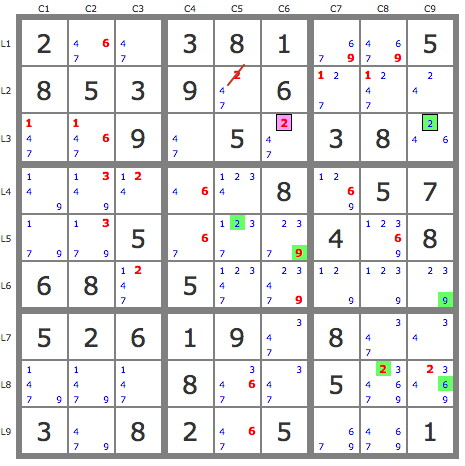
2) P'(6r1c2) : -6r1c2->6r3c2->4r3c9->4r4c4-4r6c3->7r1c3 =>-7r1c2.
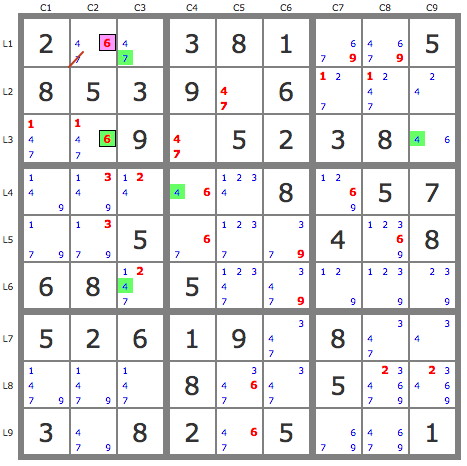
3) P'(6r1c2) : -6r1c2->6r3c2->---->4r9c2 (see diagram) => -4r1c2 => r1c2=6 and r3c9=6.
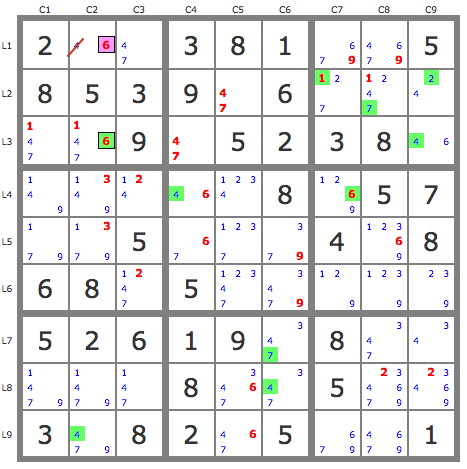
4) P'(6r9c7) : -6r9c7->6r4c7->4r4c4->4r2c5->2r2c9->2r8c8 => -6r8c8 => r8c5=6.
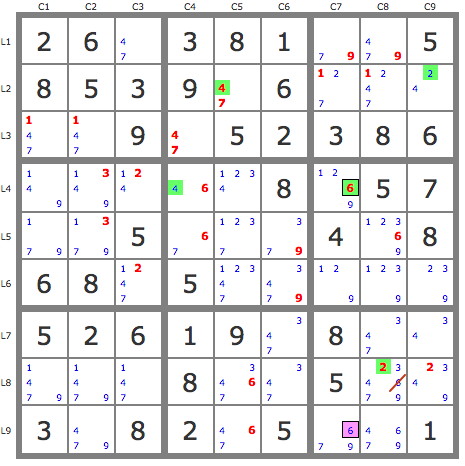
5) P'(4r3c4) : -4r3c4->4r2c5->------>7r5c4 (see diagram) => -7r3c4 => r3c4=4, stte.
1) P'(2r3c6) : -2r3c6->2r3c9->6r8c9->[9r6c9->9r5c6, 2r8c8]->2r5c5 => -2r2c5 => r3c6=2.
Hidden Text: Show

2) P'(6r1c2) : -6r1c2->6r3c2->4r3c9->4r4c4-4r6c3->7r1c3 =>-7r1c2.
Hidden Text: Show

3) P'(6r1c2) : -6r1c2->6r3c2->---->4r9c2 (see diagram) => -4r1c2 => r1c2=6 and r3c9=6.
- Code: Select all
- - - - - - - - - - - - - -
/ / \
-6r1c2->6r3c2->4r3c9->2r2c9- - - - - - - - ->1r2c7->7r2c8->7r7c6->4r8c6->4r9c2
\ / /
\ >6r4c7>79r19c7 /
\ / /
>4r4c4- - - - - - - - - - - - - - - - -
Hidden Text: Show

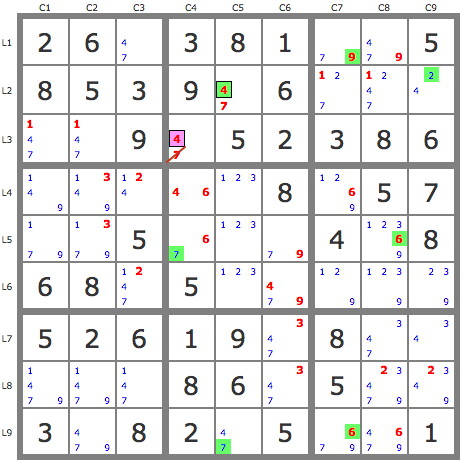
4) P'(6r9c7) : -6r9c7->6r4c7->4r4c4->4r2c5->2r2c9->2r8c8 => -6r8c8 => r8c5=6.
Hidden Text: Show

5) P'(4r3c4) : -4r3c4->4r2c5->------>7r5c4 (see diagram) => -7r3c4 => r3c4=4, stte.
- Code: Select all
-4r3c4->4r2c5->2r2c9->17r2c78->9r1c7->6r9c7->6r5c8->7r5c4
\ /
->7r9c6- - - - - - - - -
Hidden Text: Show

Hidden Text: Show