The New Sudoku Players' Forum

[Mauriès Robert]

Hi all,
This puzzle is a little harder than the previous one with a level TDP=2. It therefore requires several steps to solve it.
Good resolution.
Robert

.....7...1..2....392..8..1..5.8..4..6...7...1..1..5.3..8..4..563....9..4...6.....

Code: Select all

+-------+-------+-------+
| . . . | . . 7 | . . . |
| 1 . . | 2 . . | . . 3 |
| 9 2 . | . 8 . | . 1 . |
+-------+-------+-------+
| . 5 . | 8 . . | 4 . . |
| 6 . . | . 7 . | . . 1 |
| . . 1 | . . 5 | . 3 . |
+-------+-------+-------+
| . 8 . | . 4 . | . 5 6 |
| 3 . . | . . 9 | . . 4 |
| . . . | 6 . . | . . . |
+-------+-------+-------+


level TDP: Show

1) Valid P(8r1C9) and invalid P(8r6c9) => 14 placements.
2) P(1r8c5) valid and P(2r8c5) invalid => single solution
=> level TDP=2

[Cenoman]

A krakenless solution in six steps. Not searched the least number of steps, rather searched simple steps...

Code: Select all

 +-----------------------+-------------------------+-------------------------+
 |  458   346    34568   | c13459   1369-5  7      |  269-8   2469-8 j2589   |
 |  1     467  la58-467  |  2      b569     46     | k6789   k46789   3      |
 |  9     2      34567   | c345     8       346    |  67      1       57     |
 +-----------------------+-------------------------+-------------------------+
 | g27    5      239-7   |  8       12369   1236   |  4       2679    279    |
 |  6     349    23489   |  349     7       234    |  5       289     1      |
 | h48   h479    1       | h49      269     5      |  267-89  3      i278-9  |
 +-----------------------+-------------------------+-------------------------+
 | f27    8      29-7    | e137     4       123    |  12379   5       6      |
 |  3     167    267-5   | d57-1    125     9      |  1278    278     4      |
 |  45    1479   24579   |  6       1235    8      |  12379   279     279    |
 +-----------------------+-------------------------+-------------------------+

1. (5)r2c3 = r2c5 - r13c4 = (5*-7)r8c4 = r7c4 - r7c1 = r4c1 - (7=498)r6c124 - r6c9 = r1c9 - r2c78 = (8)r2c3 loop
=> -467 r2c3, -5 r1c5, -1 r8c4, -7 r7c3, -7 r4c3, -9 r6c79, -8 r6c7, -8 r1c78; and -5r8c3* (groupe kite sub-chain)

Code: Select all

 +-----------------------+-------------------------+-------------------------+
 |  458   346    34568   |  13459   1369    7      |  269     2469   f289-5  |
 |  1    c467    58      |  2       569     46     |  6789    46789   3      |
 |  9     2    vb34567   |  345     8       346    | u67      1      a57     |
 +-----------------------+-------------------------+-------------------------+
 |  27    5      239     |  8       12369  z1236   |  4       2679    279    |
 |  6     349    23489   |  349     7      z234    |  5       289     1      |
 | d48   d479    1       | d49     s69-2    5      | t267     3      e278    |
 +-----------------------+-------------------------+-------------------------+
 |xC27    8     C29      |  137     4      y123    | A1237-9  5       6      |
 |  3    C167  wC267     |  57      125     9      | B1278    278     4      |
 |  45    1479  w24579   |  6       123     8      | A12379   279     279    |
 +-----------------------+-------------------------+-------------------------+

2. (5=7)r3c9 - r3c3 = r2c2 - (7=498)r6c124 - r6c9 = (8)r1c9 => -5 r1c9; 1 placement (+5r3c9)

3. (31)r79c7 = r8c7 - (1=2679)b7p1356 => -9 r7c7; 1 placement (+9r7c3)

4. (6)r6c5 = r6c7 - (6=7)r3c7 - r3c3 = r89c3 - (7=2)r7c1 - r7c6 = (2)r45c6 => -2 r6c5; 17 placements

Code: Select all

 +--------------------+--------------------+-----------------+
 |  45  A346   3456   |  1     9     7     | E2-6 D24   8    |
 |  1   c4(6)7 8      |  2     5    d6-4   |  9    47   3    |
 |  9    2    b467    | a34    8    a346   |  67   1    5    |
 +--------------------+--------------------+-----------------+
 |  7    5     23     |  8     13    123   |  4    6    9    |
 |  6    349   234    |  349   7     234   |  5    8    1    |
 |  8    49    1      |  49    6     5     |  27   3    27   |
 +--------------------+--------------------+-----------------+
 |  2    8     9      |  7     4     13    |  13   5    6    |
 |  3   B167  C67     |  5     12    9     |  8   C27   4    |
 |  45   147   457    |  6     123   8     |  13   9    27   |
 +--------------------+--------------------+-----------------+

5. (4)r3c46 = (4-7)r3c3 = (7-6)r2c2 = (6)r2c6 => -4 r2c6; 1 placement (+6r2c6)

6. (6)r1c2 = r8c2 - (6=72)r8c38 - r1c8 = (2)r1c7 => -6 r1c7; ste

Edit: corrected typos

[Mauriès Robert]

Hi Cenoman,
Nice loop of the first step and nice resolution.
What is the reason for choosing the 5r2 pair to start your resolution and get to the loop?
Cordially
Robert

[Mauriès Robert]

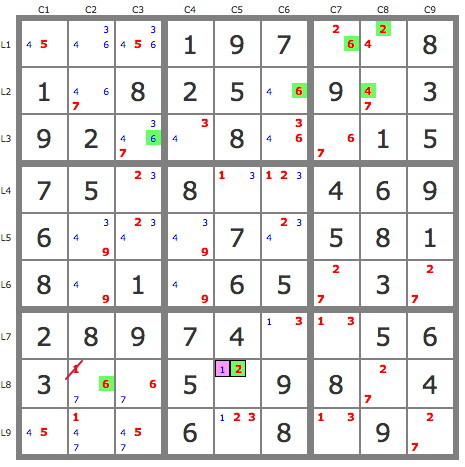
Hi all,
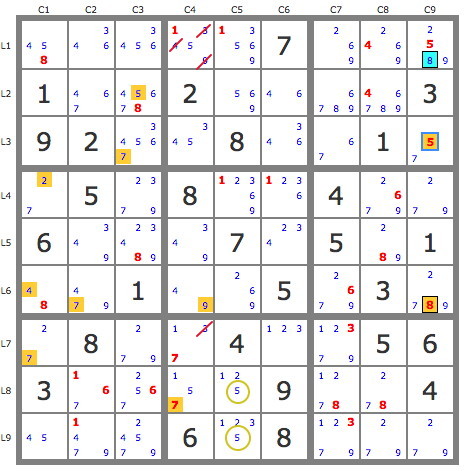
Here is my resolution with TDP, based on the exploitation of the pairs 8c9 and 8c1 which form an X-wing.

1) X-wing (8c1, 8c9) => -8r1c378 and -8r6c7. This is equivalent to P(8c1r1): 8c1r1->8r6c9 and P(8r6c1): 8r6c1->8r1c9 => -8r1c378 and -8r6c7.
But this is only a partial result that can be expanded by developing the two tracks P(8c1r1) blue and P(8r6c1) yellow, which we will do step by step, visually on the puzzle (coloring candidates).

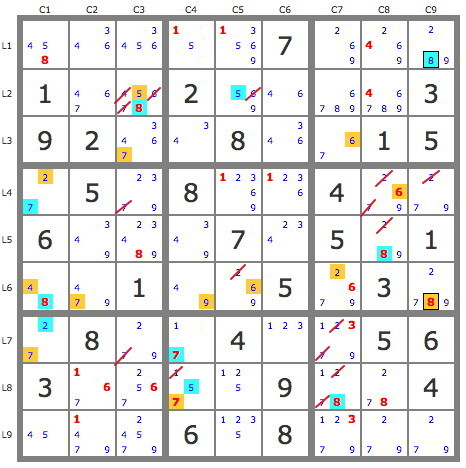
2) A first development of the two tracks (puzzle 2) allows a validation and several eliminations : -346r1c4, r3c9=5, -3r7c3.

puzzle 1: Show

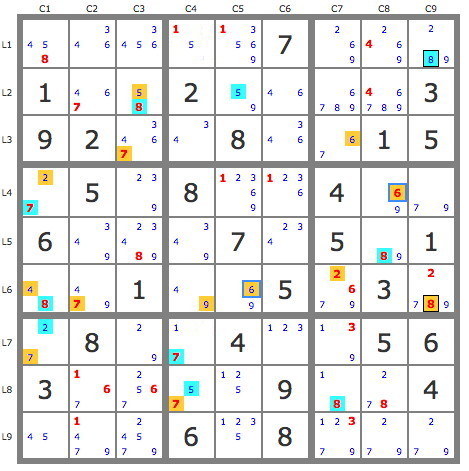
3) By developing a little more the two tracks (puzzle 3), the blue one via the 8r5c8 and the yellow one via the 6r3c7, we obtain several new eliminations (candidates crossed out in red).

puzzle 2: Show

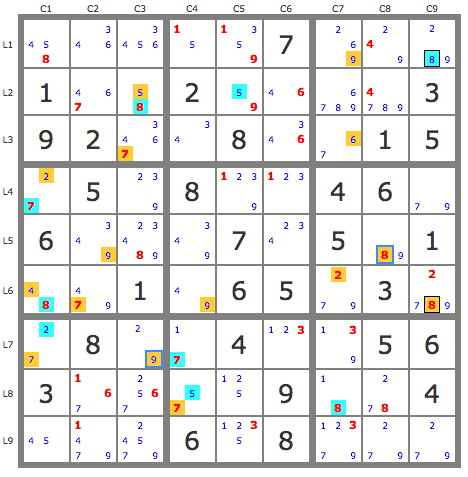
4) P(8r1c9): 8r1c9-> --- ->49r6c24->6r6c5 (puzzle 4) => validation of 6r6c5 also belonging to the yellow track. Two placements.

puzzle 4: Show

5) P(8r1c9) : 8r1c9-> --- ->9r7c3 et P(8r6c9) : 8r6c9-> --- ->9r1c7->9r7c3> --- ->9r5c2->8r5c8 (puzzle 5) => validation of 9r7c3 and 8r5c8 => 9 additional investments at the same time as the disability of P(8r6c9) is established.

puzzle 5: Show

6) Finally, we finish with the anti-track P'(1r8c5): -1r8c5-> --- -> 6r8c2 (puzzle 6) => -1r8c2, and the grid ends with the basic techniques.

puzzle 6: Show

Robert