We try to add ALS2 to an ALS-Chain that currently ends in ALS1:Collect all RCs between ALS1 and ALS2 (the Possible RCs (PRC))
If no ARC is left the chain stops with ALS1.
Subtract the Actual RCs (ARC) used to reach ALS1 from the PRCs; what's left are the new ARCs
If the chain starts with two PRCs one of them can be arbitrarily chosen as ARC
To prove the rules lets look at all possible combinations of RCs (we are only using ALS so the maximum number of RCs per ALS is 2).
1 ARC- ALS1 -1 PRC
This is only a reformulation of the rule that two adjacent RCs must not be equal.
1 ARC- ALS1 -2 PRCs
a- ALS1 -ab: b remains as new ARC, the chain can be continued.
a- ALS1 -bc: b and c are the new ARCs, the contradiction can be ignored (see below).
2 ARCs- ALS1 -1 PRC
ab- ALS1 -a: ARC a cancels PRC a, the chain cannot be continued.
ab- ALS1 -c: c becomes ARC, the contradiction can be ignored (see below).
2 ARCs- ALS1 -2 PRCs
ab- ALS1 -ab: No ARC remains, the chain stops.
ab- ALS1 -bc: c becomes ARC, the chain continues (contradiction ignored).
ab- ALS1 -cd: c and d become ARCs (contradiction ignored).
The whole thing works because the ARCs are deleted from the following ALS, thus wiping out the same candidate as possible RC for the next step.
ALS Contradiction Chains
A problem occurs when an ALS is reached via two ARCs: This leaves not enough candidates to fill all cells in the second ALS thus causing a contradiction (Allan Barker's "Locked Set" within the ALS-Chain?). For the chain this is completely irrelevant. All that matters is that the remaining candidates are locked within the ALS and thus can be used as RCs into another ALS.
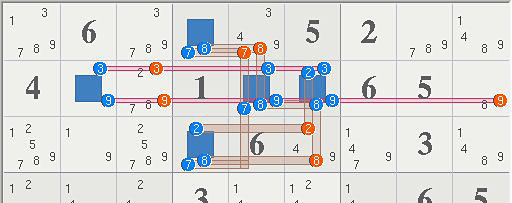
It is possible to use the contradiction in another way: If a link with two ARCs occurs, the initial premise must be invalid. This turns the initial ALS into a locked set. The same logic can be applied to all ALS in the chain. An Example (e1, e2, e3 are the remaining candidates for the respective ALS):
x- ALS1:(x|e1|a) -a- ALS2:(a|e2|b) -b- ALS3:(b|e3|cd) -cd- ALS4 => contradiction!
The contradiction proofs, that only one of c/d can be true in ALS3. That locks (b|e3) in ALS3, which in turn locks (a|e2) in ALS2 and (x|e1) in ALS1. All candidates that see the locked sets can be eliminated.
This is nothing new of course: It is simply the Doubly Linked ALS-XZ ALS3/ALS4 plus subsequent Locked Set moves combined into one (and doing the ALS-XZ first and then the Locked Sets independently could provide even more eliminations).
Reversibility
Some of the combinations of RCs produce non reversible chains. As PIsaacson already noted this is irrelevant in case of "normal" ALS chains but it is relevant for Continuous ALS Loops. Take as an example the following chain:
a- ALS1:(a|e1|b) -(a)b- ALS2:(b|e2|c) -c- ALS3:(c|e3|a) -a
The chain will eliminate all candidates a that can see all occurences of a in both ALS1 and ALS3. The problem is the double link (ab) between ALS1 and ALS2: read from left to right everything works fine. a cannot be in ALS1 which locks (e1|b). b thus cannot be in ALS2 which locks (e2|c), which in turn locks (e2|a) in ALS3. The other direction doesnt work: if a is not in ALS3, (c|e3) becomes locked which in turn locks (b|e2) in ALS2. Unfortunately e2 contains a as well which eliminates a and b from ALS1 removing the possibility to use a as RC for the next step on the left side (or put another way: ALS1<>a => ALS3=a; ALS3<>a => ALS1<>a).
My understanding of Continuous Loops is limited but I always thought that the rule that weak links become conjugate links depends on the chain beeing reversable. Perhaps someone with more experience could verify/negate that?
[edit: added start condition]