The New Sudoku Players' Forum

[Yogi]

.486..1..26.9.15.8.918..63.68.7...1..752168...1.3.8.6.83.569.21159427386.2618395.

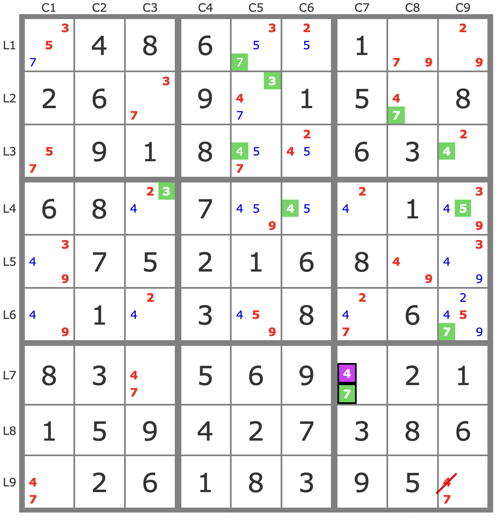
Code: Select all

+----------------+----------------+----------------+
| 357  4    8    | 6    357  25   | 1    79   279  |
| 2    6    37   | 9    347  1    | 5    47   8    |
| 57   9    1    | 8    457  245  | 6    3    247  |
+----------------+----------------+----------------+
| 6    8    234  | 7    459  45   | 24   1    3459 |
| 349  7    5    | 2    1    6    | 8    49   349  |
| 49   1    24   | 3    459  8    | 247  6    4579 |
+----------------+----------------+----------------+
| 8    3    47   | 5    6    9    | 47   2    1    |
| 1    5    9    | 4    2    7    | 3    8    6    |
| 47   2    6    | 1    8    3    | 9    5    47   |
+----------------+----------------+----------------+


I’m told the situation for a UR Type6, which instantly allows two placements, doesn’t occur very often.
Unusually here, it doesn’t lead to stte. A few more moves are required. 24URr46c37

[Mauriès Robert]

Hi Yogi,
For my part, I never eliminate by using the forbidden configurations (UR and others), because they assume the acquired uniqueness. On the other hand, I use them to start a chain (anti-track in TDP).
Here, for example, I can start with the 7r6c7 or the 3r4c3 because their simultaneous eliminations would make the UR appear.
(-7r6c7)->7r6c9->5r4c9->3r4c3->2r6c3->... => -2r6c7
or
(-3r4c3)->3r4c9->5r6c9->7r6c7->2r6c3->... => -2r4c3
These eliminations obtained in this way do not assume uniqueness.

That said, it is not useful to make these eliminations to solve, a single complex chain (anti-track in TDP) is enough:
(-4r7c7)->7r7c7->7r6c9->5r4c9->[ ( 4r4c6 and 3r4c3->3r2c5 )->4r3c5 ]->7r1c5->7r2c8->4r3c9->... => -4r9c9 => r7c7=4, stte.



Robert

[jco]

I did not address uniqueness because the following (not simple) solution called my attention (found it after extending Medusa Coloring).
After basics,

Code: Select all

.-------------------------------------------------------------.
|  357   4     8     | 6     357  F2(5)  |  1    D79   E29    |
|  2     6     37    | 9     347   1     |  5     47    8     |
| d57    9     1     | 8     457  c245   |  6     3     24    |
|--------------------+-------------------+--------------------|
|  6     8    v234   | 7     459  b45    |oB24    1 maWu3459  |
|  349   7     5     | 2     1     6     |  8   nC49    349   |
|  49    1    v24    | 3     459   8     |oB247   6     4579  |
|--------------------+-------------------+--------------------|
|  8     3    v47    | 5     6     9     |pA47    2     1     |
|  1     5     9     | 4     2     7     |  3     8     6     |
|dw47    2     6     | 1     8     3     |  9     5     7-4   |
'-------------------------------------------------------------'

Almost Kraken Cell

(4)r7c7 = r46c7 - (4=9)r5c8 - r1c8 = (9-2)r1c9 = (2-5*)r1c6 = Kraken Cell => -4 r9c9; ste

where

Code: Select all

Kraken Cell (3459)r4c9
(3)r4c9 - (3=247)r467c3 - (7=4)r9c1       (uvw)
(4)r4c9                                   (W)
(5)r4c9 - r4c6 *=* (5)r3c6 - (5=74)r39c1  (abcd)
(9)r4c9 - (9=4)r5c8 - (4)r46c7 = (4)r7c7  (mnop)

Thanks for the puzzle!

[jco]

I have been studying this puzzle some more and found another way (krakenless).
After basics.

Code: Select all

.-----------------------------------------------------------.
|a357   4     8     | 6     37-5 k2-5   | 1    j79   j29    |
| 2     6    h37    | 9     347   1     | 5    i47    8     |
|b57    9     1     | 8     457   245   | 6     3     24    |
|-------------------+-------------------+-------------------|
| 6     8    g234   | 7     459  g45    |g24    1     3459  |
| 349   7     5     | 2     1     6     | 8     49    349   |
| 49    1     24    | 3    f459   8     | 247   6    e4579  |
|-------------------+-------------------+-------------------|
| 8     3     47    | 5     6     9     | 47    2     1     |
| 1     5     9     | 4     2     7     | 3     8     6     |
|c47    2     6     | 1     8     3     | 9     5    d47    |
'-----------------------------------------------------------'

1. (5)r1c1 = (5-7)r3c1 = r9c1 - r9c9 = (7-5)r6c9 = (5*)r6c5 - (5=423)r4c673 - (3=7)r2c3 - r2c8 = (79-2)r1c89 = (2)r1c6

=> -5* r1c5, -5 r1c6; ste