The New Sudoku Players' Forum

[yzfwsf]

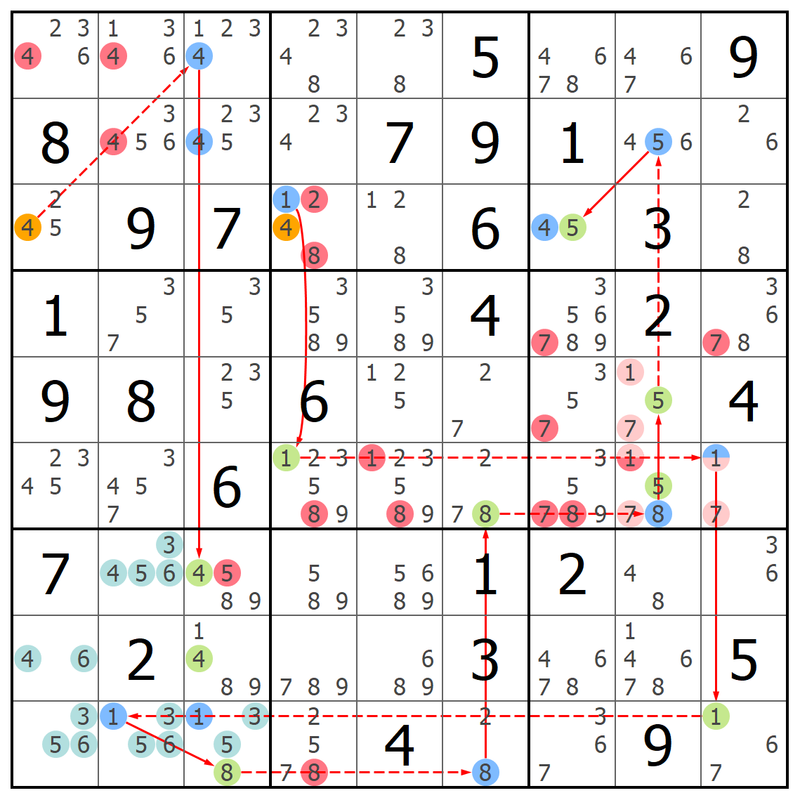
Code: Select all

,------------------,---------------------,---------------------,
| 2346  1346  1234 | 2348    238     5   | 4678    467    9    |
| 8     3456  2345 | 234     7       9   | 1       456    26   |
| 245   9     7    | 1248    128     6   | 45      3      28   |
:------------------+---------------------+---------------------:
| 1     357   35   | 3589    3589    4   | 356789  2      3678 |
| 9     8     235  | 6       125     27  | 357     157    4    |
| 2345  3457  6    | 123589  123589  278 | 35789   1578   17   |
:------------------+---------------------+---------------------:
| 7     3456  4589 | 589     5689    1   | 2       48     36   |
| 46    2     1489 | 789     689     3   | 4678    14678  5    |
| 356   1356  1358 | 2578    4       28  | 367     9      167  |
'------------------'---------------------'---------------------'

My solver can find a zero rank structure under the current PM. Is there any other solver that can find this structure or other equivalent structures？

[marek stefanik]

Found one manually:

Code: Select all

,------------------,---------------------,---------------------,
| 236–4 136–4 b1234| 2348    238     5   | 4678    467    9    |
| 8     356–4 b2345| 234     7       9   | 1      β456    26   |
|a245   9     7    |A14–28  B128     6   |α45      3      28   |
:------------------+---------------------+---------------------:
| 1     357   35   | 3589    3589    4   | 35689–7 2      368–7|
| 9     8     235  | 6      C125     27  | 35–7  Dγ157    4    |
| 2345  3457  6    | 12359–8 2359–18 δ278| 359–78 γ578–1 Eγ17  |
:------------------+---------------------+---------------------:
| 7     3456 #489–5| 589     5689    1   | 2       48     36   |
| 46    2    #1489 | 789     689     3   | 4678    14678  5    |
| 356  G1356 Gζ1358| 257–8   4      ε28  | 367     9     F167  |
'------------------'---------------------'---------------------'
Mapping 4r3 -> x9r78c3:
4r3c1 – 4r12c3 = 49r78c3
(4–1)r3c4 = 1r3c5 – 1r5c5 = 1r5c8 – 1r6c9 = 1r9c9 – 1r9c23 = 19r78c3
(4–5)r3c7 = 5r2c8 – (5=178)b6p589 – 8r6c6 = 8r9c6 - 8r9c3 = 89r78c3

Truths and links: Show

13 Truths = {1R35 4R3 489C3 8C6 1C9 56N8 6N9 1B7 5B3}
12 Links = {1r9 8r69 1c5 5c8 78n3 3n4 3n7 4b1 17b6}

1b6p59 are part of two truths, so the link 1b6 has to be doubled for a full cover (1b6p8 is only part of one truth, so it's a cannibalistic elim).

The puzzle still remains difficult (9.0 -> 8.5 skfr).

Marek

Edit: Corrected a typo. Thanks yzfwsf.

[yzfwsf]

Great, there are 13 truths and 14 truths from the solver.

[yzfwsf]

Region Type Blossom Loop: 4r3c147 => r6c58 <> 1, r3c4 <> 2, b1p125 <> 4, r7c3 <> 5, b6p1347 <> 7, r6c457,r39c4 <> 8
(4-1)r3c4 = r6c4 - r6c9 = r9c9 - (1=34568)b7p24789 - r9c6 = r6c6 - (8=175)b6p589 - r2c8 = (5-4)r3c7
4r3c1 - r12c3 = 4r78c3

The idea of the program is to find a burr ring, and then find branches for the burr, with the branch endpoint located in the weak area of the burr ring or other branches.

[Leren]

Well I'm just a beginner on this move but there appears to be some bugs in your diagram.

1. According to your main chain the 4 in r3c4 should be light green (assumed True).

2. In r6c89 the dashed line seems to have created bi-color candidates. I think the 1 in r6c8 should be all pink (in the 3 cell ALS) and in r6c9 should be all blue (False).

3. The small chain on the second line seems to be the wrong way around. It would make more sense to me to write :

Code: Select all

.......(1=34568)b7p24789\
                         \ - 4 r78c3 = r12c3 - r3c1

So the 4's in r78c3 should be blue (False), those in r12c3 should be Green (True) and in r3c1 should be blue (False).

Leren

[yzfwsf]

Hi:Leren
4r3c4 is the starting point of the main loop, and in my solver, the starting point is orange.
The reason why 1r6c8 is bicolored is because it is both a part of elimination and a part of ALS nodes.
The reason why 1r6c9 is bicolored is because it serves as both an independent node and a part of the ALS node.
A small chain is a branch that starts at the same house (same candidate) or cell (different candidate) as the starting point of the main chain. Its endpoint is not unique, as long as it is located in a weak area of the main chain or other branches.
If the starting point of a branch happens to be on the weak region of the main chain or other branches, we will no longer need to find a branch for it.