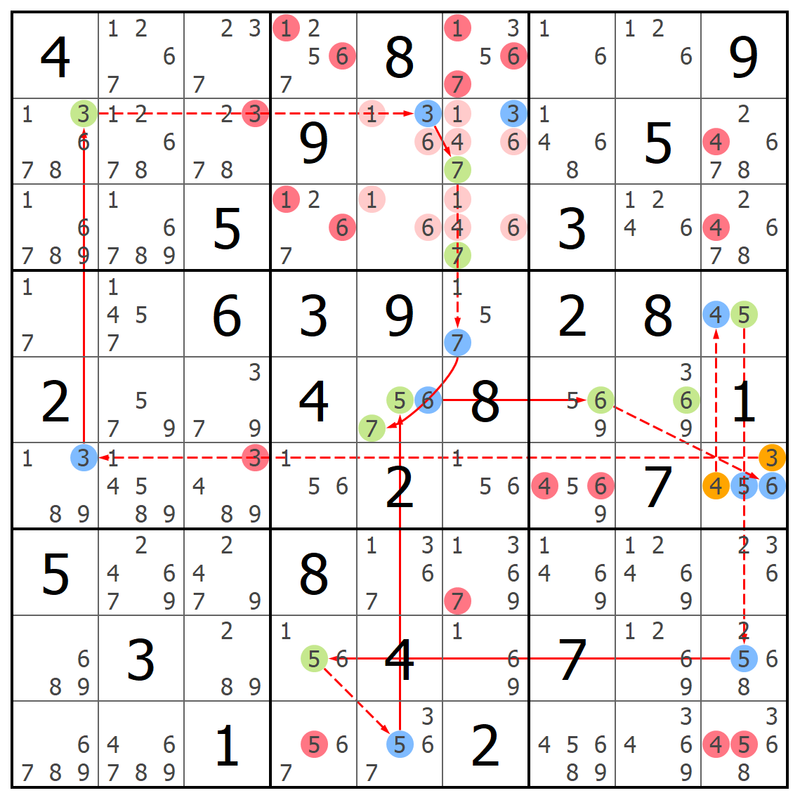
- Code: Select all
,--------------------,--------------------,---------------------,
| 4 1267 237 | 12567 8 13567 | 16 126 9 |
| 13678 12678 2378 | 9 136 13467 | 1468 5 24678 |
| 16789 16789 5 | 1267 16 1467 | 3 1246 24678 |
:--------------------+--------------------+---------------------:
| 17 1457 6 | 3 9 157 | 2 8 45 |
| 2 579 379 | 4 567 8 | 569 369 1 |
| 1389 14589 3489 | 156 2 156 | 4569 7 3456 |
:--------------------+--------------------+---------------------:
| 5 24679 2479 | 8 1367 13679 | 1469 12469 236 |
| 689 3 289 | 156 4 169 | 7 1269 2568 |
| 6789 46789 1 | 567 3567 2 | 45689 3469 34568 |
'--------------------'--------------------'---------------------'
My solver found a 17 elimination Blossom Loop on the current PM.