The New Sudoku Players' Forum

[denis_berthier]

.
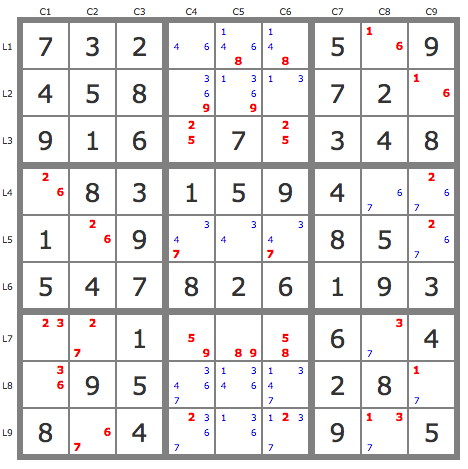
Here is another nice visual pattern, the pyramid, with a moderately difficult (SER 8.4) puzzle:

Code: Select all

X . . . . . . . X
. X . . . . . X.
. . X . . . X . .
. . X X X X X . .
. . X . . . X . .
. . X X X X X . .
. . X . . . X . .
. X . . . . . X.
X . . . . . . . X


Code: Select all

+-------+-------+-------+
! 7 . . ! . . . ! . . 9 !
! . 5 . ! . . . ! . 2 . !
! . . 6 ! . . . ! 3 . . !
+-------+-------+-------+
! . . 3 ! 1 5 9 ! 4 . . !
! . . 9 ! . . . ! 8 . . !
! . . 7 ! 8 2 6 ! 1 . . !
+-------+-------+-------+
! . . 1 ! . . . ! 6 . . !
! . 9 . ! . . . ! . 8 . !
! 8 . . ! . . . ! . . 5 !
+-------+-------+-------+

7.......9.5.....2...6...3....31594....9...8....78261....1...6...9.....8.8.......5 # 95227 FNBHYK C24.M/S4.hv
SER 8.4

When repeated, the pattern gives an irregular tiling of the plane (with 3 different tile types: 1 square, two different hexagons). It's not as nice as the double lozenge tiling, but it also gives a stereographic effect.

Code: Select all

X . . . . . . . X X . . . . . . . X X . . . . . . . X X . . . . . . . X X . . . . . . . X X . . . . . . . X
. X . . . . . X . . X . . . . . X . . X . . . . . X . . X . . . . . X . . X . . . . . X . . X . . . . . X .
. . X . . . X . . . . X . . . X . . . . X . . . X . . . . X . . . X . . . . X . . . X . . . . X . . . X . .
. . X X X X X . . . . X X X X X . . . . X X X X X . . . . X X X X X . . . . X X X X X . . . . X X X X X . .
. . X . . . X . . . . X . . . X . . . . X . . . X . . . . X . . . X . . . . X . . . X . . . . X . . . X . .
. . X X X X X . . . . X X X X X . . . . X X X X X . . . . X X X X X . . . . X X X X X . . . . X X X X X . .
. . X . . . X . . . . X . . . X . . . . X . . . X . . . . X . . . X . . . . X . . . X . . . . X . . . X . .
. X . . . . . X . . X . . . . . X . . X . . . . . X . . X . . . . . X . . X . . . . . X . . X . . . . . X .
X . . . . . . . X X . . . . . . . X X . . . . . . . X X . . . . . . . X X . . . . . . . X X . . . . . . . X
X . . . . . . . X X . . . . . . . X X . . . . . . . X X . . . . . . . X X . . . . . . . X X . . . . . . . X
. X . . . . . X . . X . . . . . X . . X . . . . . X . . X . . . . . X . . X . . . . . X . . X . . . . . X .
. . X . . . X . . . . X . . . X . . . . X . . . X . . . . X . . . X . . . . X . . . X . . . . X . . . X . .
. . X X X X X . . . . X X X X X . . . . X X X X X . . . . X X X X X . . . . X X X X X . . . . X X X X X . .
. . X . . . X . . . . X . . . X . . . . X . . . X . . . . X . . . X . . . . X . . . X . . . . X . . . X . .
. . X X X X X . . . . X X X X X . . . . X X X X X . . . . X X X X X . . . . X X X X X . . . . X X X X X . .
. . X . . . X . . . . X . . . X . . . . X . . . X . . . . X . . . X . . . . X . . . X . . . . X . . . X . .
. X . . . . . X . . X . . . . . X . . X . . . . . X . . X . . . . . X . . X . . . . . X . . X . . . . . X .
X . . . . . . . X X . . . . . . . X X . . . . . . . X X . . . . . . . X X . . . . . . . X X . . . . . . . X
X . . . . . . . X X . . . . . . . X X . . . . . . . X X . . . . . . . X X . . . . . . . X X . . . . . . . X
. X . . . . . X . . X . . . . . X . . X . . . . . X . . X . . . . . X . . X . . . . . X . . X . . . . . X .
. . X . . . X . . . . X . . . X . . . . X . . . X . . . . X . . . X . . . . X . . . X . . . . X . . . X . .
. . X X X X X . . . . X X X X X . . . . X X X X X . . . . X X X X X . . . . X X X X X . . . . X X X X X . .
. . X . . . X . . . . X . . . X . . . . X . . . X . . . . X . . . X . . . . X . . . X . . . . X . . . X . .
. . X X X X X . . . . X X X X X . . . . X X X X X . . . . X X X X X . . . . X X X X X . . . . X X X X X . .
. . X . . . X . . . . X . . . X . . . . X . . . X . . . . X . . . X . . . . X . . . X . . . . X . . . X . .
. X . . . . . X . . X . . . . . X . . X . . . . . X . . X . . . . . X . . X . . . . . X . . X . . . . . X .
X . . . . . . . X X . . . . . . . X X . . . . . . . X X . . . . . . . X X . . . . . . . X X . . . . . . . X
.

[Edit] As remarked by JPF below, this pattern has no minimal puzzle.

[Mauriès Robert]

Hi all,
Here is a two-step solution to this puzzle after reduction using the basic techniques.

puzzle: Show

Step 1
P(6r1c5) : [6r1c5->8r1c6->5r7c6->2r3c6->2r9c4]->6r8c4->6r4c1->...
=> 6c8=∅ => r1c5≠6
Step 2
P(6r1c4) : [(6r1c4->1r1c8->6r4c8->6r5c2)->6r9c5]->
1r9c6->2r3c6->5r7c6->9r7c4->9r2c5->...
=> 1b2=∅ => r1c4≠6 => r1c8=6, stte.
Robert

[denis_berthier]

.
A solution in Z6.
It starts with some cleaning of the PM:

Code: Select all

***********************************************************************************************
***  SudoRules 20.1.s based on CSP-Rules 2.1.s, config = W+SFin
***  Using CLIPS 6.32-r779
***********************************************************************************************
singles ==> r6c9 = 3, r6c2 = 4, r6c1 = 5, r6c8 = 9, r2c7 = 7, r8c7 = 2,> r9c7 = 9, r1c7 = 5, r8c3 = 5, r5c8 = 5, r4c2 = 8
182 candidates, 1134 csp-links and 1134 links. Density = 6.88%
whip[1]: r4n7{c9 .} ==> r5c9 ≠ 7
hidden-triplets-in-a-row: r7{n5 n8 n9}{c4 c6 c5} ==> r7c6 ≠ 7, r7c6 ≠ 4, r7c6 ≠ 3, r7c6 ≠ 2, r7c5 ≠ 7, r7c5 ≠ 4, r7c5 ≠ 3, r7c4 ≠ 7, r7c4 ≠ 4, r7c4 ≠ 3, r7c4 ≠ 2
whip[1]: b8n2{r9c6 .} ==> r9c2 ≠ 2, r9c3 ≠ 2
singles ==> r9c3 = 4, r2c3 = 8, r1c3 = 2, r3c2 = 1, r1c2 = 3, r3c8 = 4, r3c1 = 9, r2c1 = 4, r3c9 = 8, r3c5 = 7, r7c9 = 4, r5c1 = 1

leading to the following resolution state:

Code: Select all

   7 3 2 46 1468 148 5 16 9
   4 5 8 369 1369 13 7 2 16
   9 1 6 25 7 25 3 4 8
   26 8 3 1 5 9 4 67 267
   1 26 9 347 34 347 8 5 26
   5 4 7 8 2 6 1 9 3
   23 27 1 59 89 58 6 37 4
   36 9 5 3467 1346 1347 2 8 17
   8 67 4 2367 136 1237 9 137 5


The difference with Robert's PM is the absence of n7r5c9 (eliminated by a whip[1] at the start)

The resolution path continues in Z6 (i.e. using only reversible chains):

Code: Select all

biv-chain[3]: r9c2{n7 n6} - b4n6{r5c2 r4c1} - r4c8{n6 n7} ==> r9c8 ≠ 7
biv-chain[3]: r9c8{n3 n1} - c9n1{r8 r2} - r2c6{n1 n3} ==> r9c6 ≠ 3
biv-chain-rn[4]: r4n2{c9 c1} - r7n2{c1 c2} - r7n7{c2 c8} - r4n7{c8 c9} ==> r4c9 ≠ 6
z-chain[4]: r9c8{n3 n1} - r9c5{n1 n6} - b7n6{r9c2 r8c1} - r8n3{c1 .} ==> r9c4 ≠ 3
z-chain[6]: r9n2{c6 c4} - r3c4{n2 n5} - r7c4{n5 n9} - c5n9{r7 r2} - c5n1{r2 r1} - c8n1{r1 .} ==> r9c6 ≠ 1
hidden-pairs-in-a-row: r9{n1 n3}{c5 c8} ==> r9c5 ≠ 6
finned-x-wing-in-columns: n1{c9 c6}{r8 r2} ==> r2c5 ≠ 1
biv-chain[3]: r9n6{c4 c2} - c1n6{r8 r4} - c8n6{r4 r1} ==> r1c4 ≠ 6
naked-single ==> r1c4 = 4
biv-chain[3]: c6n4{r8 r5} - r5c5{n4 n3} - r9c5{n3 n1} ==> r8c6 ≠ 1
whip[1]: b8n1{r9c5 .} ==> r1c5 ≠ 1
biv-chain[3]: r1c5{n6 n8} - r7c5{n8 n9} - b2n9{r2c5 r2c4} ==> r2c4 ≠ 6
whip[1]: c4n6{r9 .} ==> r8c5 ≠ 6
naked-triplets-in-a-column: c5{r5 r8 r9}{n3 n4 n1} ==> r2c5 ≠ 3
biv-chain[4]: r9n3{c5 c8} - b9n1{r9c8 r8c9} - r2n1{c9 c6} - b2n3{r2c6 r2c4} ==> r8c4 ≠ 3
naked-triplets-in-a-block: b8{r8c4 r9c4 r9c6}{n7 n6 n2} ==> r8c6 ≠ 7
biv-chain-rn[4]: r5n4{c5 c6} - r5n7{c6 c4} - r8n7{c4 c9} - r8n1{c9 c5} ==> r8c5 ≠ 4
singles ==> r8c6 = 4, r5c5 = 4
biv-chain[4]: r8c9{n7 n1} - r2n1{c9 c6} - c6n3{r2 r5} - c6n7{r5 r9} ==> r8c4 ≠ 7
stte

Activating whips doesn't lead to a smaller rating.

[JPF]

.
Here is another nice visual pattern, the pyramid, with a moderately difficult (SER 8.4) puzzle:

Code: Select all

X . . . . . . . X
. X . . . . . X.
. . X . . . X . .
. . X X X X X . .
. . X . . . X . .
. . X X X X X . .
. . X . . . X . .
. X . . . . . X.
X . . . . . . . X


nice pattern certainly, but which does not contain minimal puzzles.
See here Mauricio's proof.

JPF

[denis_berthier]

.Here is another nice visual pattern, the pyramid, with a moderately difficult (SER 8.4) puzzle:

Code: Select all

X . . . . . . . X
. X . . . . . X.
. . X . . . X . .
. . X X X X X . .
. . X . . . X . .
. . X X X X X . .
. . X . . . X . .
. X . . . . . X.
X . . . . . . . X

nice pattern certainly, but which does not contain minimal puzzles.
See here Mauricio's proof.
JPF

You're right to mention this. I had forgotten to do it in the first post. I'll add this information.
It's worth noticing also that Mauricio's proof is very simple.