The New Sudoku Players' Forum

[P.O.]

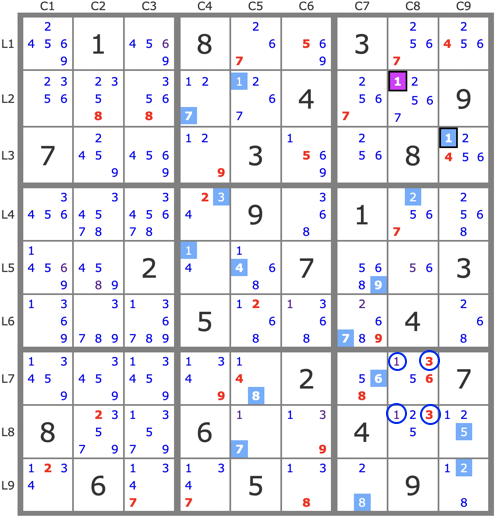
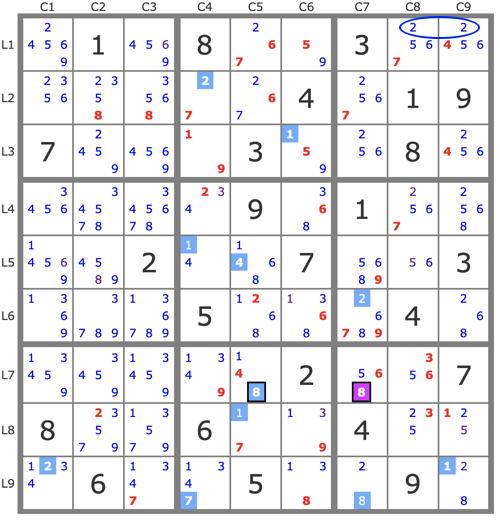
Code: Select all

once again 2 forcing chains for this one but a bit more complicated;

. 1 .   8 . .   3 . .
. . .   . . 4   . . 9
7 . .   . 3 .   . 8 .
. . .   . 9 .   1 . .
. . 2   . . 7   . . 3
. . .   5 . .   . 4 .
. . .   . . 2   . . 7
8 . .   6 . .   4 . .
. 6 .   . 5 .   . 9 .

.1.8..3.......4..97...3..8.....9.1....2..7..3...5...4......2..78..6..4...6..5..9.

24569   1       4569    8       267     569     3       2567    2456             
2356    2358    3568    127     1267    4       2567    12567   9               
7       2459    4569    129     3       1569    256     8       12456           
3456    34578   345678  234     9       368     1       2567    2568             
14569   4589    2       14      1468    7       5689    56      3               
1369    3789    136789  5       1268    1368    26789   4       268             
13459   3459    13459   1349    148     2       568     1356    7               
8       23579   13579   6       17      139     4       1235    125             
1234    6       1347    1347    5       138     28      9       128       


[Mauriès Robert]

Hi P.O.,
Here are the two steps that correspond to forcing chains that you announce.
In these sequences "->" is an implication with memory of previous implications.

1) (-1r2c8)->1r3c9->13r78c8->6r7c7->5r8c9->8r7c5->4r5c5->1r5c4->1r2c5->7r8c5->7r2c4->7r6c7->9r5c7->8r9c7->2r9c9->2r4c8->3r4c4->UR(68b5c6,b6c9) => r2c8=1 + basics.

puzzle1: Show

2 (-8r7c7)->8r7c5->4r5c5->1r5c4->1r3c6->1r8c5->7r9c4->2r2c4->1r9c9->8r9c7->2r9c1->2r1c8->2r1c9->2r6c7->... => 2b5 empty => r7c7=8, stte.

puzzle2: Show

Robert

[DEFISE]

No initial basics.

g-whip[7]: r9c7{n2 n8}- r9c9{n8 n1}- r9c6{n1 n3}- c4n3{r9 r4}- b5n2{r4c4 r6c5}- r1n2{c5 c89}- c7n2{r2 .} => -2r9c1
Single(s): 2r8c2
Box/Line: 7c2b4 => -7r4c3 -7r6c3
g-whip[6]: r1n7{c8 c5}- r8n7{c5 c3}- r8n9{c3 c6}- c4n9{r7 r3}- r3n2{c4 c79}- c8n2{r1 .} => -7r4c8
Single(s): 7r4c2, 7r6c7, 9r5c7
Box/Line: 8c7b9 => -8r9c9
whip[8]: c1n2{r2 r1}- b2n2{r1c5 r3c4}- c4n9{r3 r7}- r8n9{c6 c3}- r1n9{c3 c6}- c6n5{r1 r3}- c7n5{r3 r7}- r8n5{c8 .} => -2r2c7
whip[5]: c7n2{r3 r9}- r9c9{n2 n1}- r3n1{c9 c6}- c6n5{r3 r1}- b2n9{r1c6 .} => -2r3c4
Box/Line: 2r3b3 => -2r1c8 -2r1c9 -2r2c8
STTE

[P.O.]

hi Robert, DEFISE thank you for your answers, they always are interesting and i like to read them;
this puzzle is a bit challenging to find a shortest solution because its simplest path is relatively long and has many eliminations; also it has no 1-antibackdoor (after singles and intersections) and it's 3 1-backdoors cannot be used 'logically';
concerning Robert's solution as we add the uniqueness of the solution to the sudoku rules it is clever to use an UR to prove a contradiction; and concerning the whips it is always (still) surprising to see how operational the z-candidate idea is, i haven't seriously thought about implementing them yet but it's in the back of my mind;
so here is my solution:

Code: Select all

r8n2c289 => r2c2 r3c2 r9c1 <> 2
 r8c2=2 -
 r8c8=2 - r9c679n138 - c4n3{r79 r4} - b5n2{r4c4 r6c5} - b6n2{r6c79 r4c9} - r1n2{c9 c1}
 r8c9=2 - r9c679n138 - c4n3{r79 r4} - b5n2{r4c4 r6c5} - b6n2{r6c7  r4c8} - r1n2{c8 c1}

single: n2r8c2
intersection: c3n7r89 => r4c3 r6c3 <> 7

r3c7n256 => r3c4 <> 2
 r3c7=2 -
 r3c7=5 - c6n5{r3 r1} - b2n9{r1c6 r3c46} - b1{r1c3r3c23}{n469} - r8n9{c3 c6} - c4n9{r7 r3}
 r3c7=6 - r7n6{c7 c8} - c8n3{r7 r8} - c8n1{r8 r2} - b2{r1c5r2c45}{n267} -

intersection: r3n2c79 => r1c8 r1c9 r2c7 r2c8 <> 2
ste.