The New Sudoku Players' Forum

[P.O.]

Code: Select all

. 8 9   . . .   . . .
7 . .   2 . 9   . . .
6 . .   3 . 5   . . .
. 5 4   . . .   9 . .
. . .   . . .   2 3 .
. . .   . . 1   . . .
. 7 .   9 . .   . . 5
3 . .   . . .   7 6 .
. 4 1   . . .   . . .

.89......7..2.9...6..3.5....54...9........23......1....7.9....53.....76..41......

after basics:

4     8     9     167   167   67    35    25    23             
7     3     5     2     48    9     1468  148   1468           
6     1     2     3     48    5     48    79    79             
18    5     4     678   23    23    9     178   1678           
189   6     7     458   59    48    2     3     148           
89    2     3     4678  679   1     4568  4578  4678           
2     7     6     9     13    348   1348  148   5             
3     9     8     145   125   24    7     6     124           
5     4     1     678   2367  67    38    289   2389 


[Cenoman]

Code: Select all

 +------------------+----------------------+-----------------------+
 |  4     8    9    |  167    167    67    |  35     25     23     |
 |  7     3    5    |  2      48     9     |  1468   148    1468   |
 |  6     1    2    |  3      48     5     |  48     79     79     |
 +------------------+----------------------+-----------------------+
 |  18    5    4    |  678    23     23    |  9      178    1678   |
 |  189   6    7    |GE458y   59    E48x   |  2      3     D148    |
 |  89    2    3    | F4678y  679    1     |  4568   4578   4678   |
 +------------------+----------------------+-----------------------+
 |  2     7    6    |  9     b13   Aa348w  | B1348  B148    5      |
 |  3     9    8    | G45z-1  125    24    |  7      6     C124    |
 |  5     4    1    |  678    2367   67    |  38     289    2389   |
 +------------------+----------------------+-----------------------+

1. Kraken cell (348)r7c6
(3)r7c6 - (3=1)r7c5
(4)r7c6 - r7c78 = r8c9 - r5c9 = r5c46 - r6c4 = (45)r58c4
(8)r7c6 - (8=4)r5c6 - r56c4 = (4)r8c4
=> -1 r8c4; 1 placement

Code: Select all

 +------------------+----------------------+-----------------------+
 |  4     8    9    |  1      67*    67*   |  35     25     23     |
 |  7     3    5    |  2      48     9     |  1468   148    1468   |
 |  6     1    2    |  3      48     5     |  48     79     79     |
 +------------------+----------------------+-----------------------+
 |  18    5    4    |  678    23     23    |  9      178    1678   |
 |  189   6    7    |  458    59     48    |  2      3      148    |
 |  89    2    3    |  4678   679    1     |  4568   4578   4678   |
 +------------------+----------------------+-----------------------+
 |  2     7    6    |  9      13     348   |  1348   148    5      |
 |  3     9    8    |  45     125    24    |  7      6      124    |
 |  5     4    1    | #67-8   2367*  67*   |  38     289    2389   |
 +------------------+----------------------+-----------------------+

2. UR (67)r19c56 using externals
(6==7)r9c4 => -8 r9c4; ste

[jco]

After basics

Code: Select all

.-------------------------------------------------------------.
| 4     8     9     |  167    167   67    | 35    25    23    |
| 7     3     5     |  2      48    9     | 1468  148   1468  |
| 6     1     2     |  3      48    5     | 48    79    79    |
|-------------------+---------------------+-------------------|
|f18    5     4     |  678    2-3  l23    | 9    e178  d1678  |
|g189   6     7     |  458   h59    48    | 2     3    d148   |
| 89    2     3     |  4678   679   1     | 4568  4578  4678  |
|-------------------+---------------------+-------------------|
| 2     7     6     |  9    aA13    348   |b1348 b148   5     |
| 3     9     8     |jB45(1) i125  k24    | 7     6    c124   |
| 5     4     1     |  678    2367  67    | 38    289   2389  |
'-------------------------------------------------------------'


1. (3=1)r7c5 - (1*)r8c4 = CH => -3 r4c5 [11 placements & basics]

where CH denotes the chain (a ... l):

(3=1)r7c5 - r7c78 = r8c9 -r45c9 = r4c8 - r4c1 = (1-9)r5c1 = (9-5)r5c5 = (5)r8c5 - (5*=*4)r8c4 - (4=2)r8c6 - (2=3)r4c6
----

Code: Select all

-------------------------------------------------------------.
| 4     8     9     | 167   167   67    |  5      2     3     |
| 7     3     5     | 2     48    9     |  16-48 a48-1  168-4 |
| 6     1     2     | 3     48    5     | d48     7     9     |
|-------------------+-------------------+---------------------|
| 18    5     4     | 67    2     3     |  9      18    67    |
| 189   6     7     | 458   59    48    |  2      3     148   |
| 89    2     3     | 4678  679   1     |  46-8   5     4678  |
|-------------------+-------------------+---------------------|
| 2     7     6     | 9     13    48    | c1348  b148   5     |
| 3     9     8     | 145   15    2     |  7      6     14    |
| 5     4     1     | 678   367   67    | c38     9     2     |
'-------------------------------------------------------------'


2. Loop (4)r2c8 = (4-8)r7c8 = (8)r79c7 - (8=4)r3c7 - (4)r2c8

=> - 1 r7c8, -8 r26c7, -4 r2c79 [7 placements & basics]
----

Code: Select all

.-----------------------------------------------------------.
| 4     8     9     | 167   167   67    | 5     2     3     |
| 7     3     5     | 2     48    9     | 16    48    16    |
| 6     1     2     | 3     48    5     | 48    7     9     |
|-------------------+-------------------+-------------------|
| 8     5     4     | 67    2     3     | 9     1     67    |
| 1     6     7     | 5     9    b48    | 2     3    a48    |
| 9     2     3     | 48    67    1     | 46    5     4678  |
|-------------------+-------------------+-------------------|
| 2     7     6     | 9     13   c48    | 13   d48    5     |
| 3     9     8     | 14    5     2     | 7     6     1-4   |
| 5     4     1     | 678   367   67    | 38    9     2     |
'-----------------------------------------------------------'

3. SS(4): r5c9 - r5c6 = r7c6 = r7c8 => -4 r8c9; ste

Edit: I changed the naming for move 1. The actual (almost) discontinuous loop (DL) in move 1 was related to the placement of 3 at r4c6 (the start and end of the loop, the way the elimination was found). Since I changed that in writing the move, the reference to DL no longer makes sense.

[DEFISE]

14 Singles
Box/Line: 5r5b5 => -5r6c4 -5r6c5
Box/Line: 4b2c5 => -4r5c5 -4r6c5 -4r7c5 -4r8c5
Box/Line: 8b2c5 => -8r4c5 -8r5c5 -8r6c5 -8r7c5 -8r9c5
Hidden pairs: 23r4c56 => -6r4c5 -7r4c5 -6r4c6 -7r4c6 -8r4c6
Hidden pairs: 48c5r23 => -1r2c5 -6r2c5 -7r3c5
Box/Line: 1r2b3 => -1r1c7 -1r1c8 -1r1c9
Box/Line: 6r2b3 => -6r1c7 -6r1c9
Box/Line: 7r3b3 => -7r1c8 -7r1c9
Naked pairs: 48r3c57 => -4r3c8 -8r3c8 -4r3c9 -8r3c9
Hidden pairs: 67c6r19 => -2r9c6 -3r9c6 -8r9c6
whip[4]: r4c5{n2 n3}- r7c5{n3 n1}- r8n1{c5 c9}- r8n2{c9 .} => -2r9c5
Box/Line: 2r9b9 => -2r8c9
Hidden pairs: 29r9c89 => -8r9c8 -3r9c9 -8r9c9
Single(s): 3r1c9, 5r1c7, 2r1c8, 9r9c8, 7r3c8, 9r3c9, 2r9c9, 5r6c8
Naked pairs: 18r4c18 => -8r4c4 -1r4c9 -8r4c9
whip[5]: r3c7{n4 n8}- b9n8{r7c7 r7c8}- r4c8{n8 n1}- r5c9{n1 n8}- c6n8{r5 .} => -4r6c7
Box/Line: 4b6c9 => -4r2c9 -4r8c9
STTE

[P.O.]

thank you for your answers, here is my solution, 2 forcing chains + basics:

r7n8{c6c7c8} => r2c8 <> 1
r7c6=8 - r5c6{n8 n4} - c4n4{r5r6 r8} - r8n5{c4 c5} - r8n1{c5 c9} - b6n1{r4c9r5c9 r4c8}
r7c7=8 - c7n1{r7 r2}
r7c8=8 - r9c7{n8 n3} - r1c7{n3 n5} - c8n5{r1 r6} - c8n4{r6r2}

r8c9{n1n2n4} => r5c9 r8c6 <> 4
r8c9=1 - r5n1{c9 c1} - r5n9{c1 c5} - r5n5{c5 c4} - r8c4{n1n5 n4} - c6n4{r7r8 r5}
r8c9=2 - r9{c7c8c9}{n3n8n9} - b8n8{r9c4 r7c6} - r5c6{n8 n4}
r8c9=4 -

bte.

[Mauriès Robert]

Hi all,
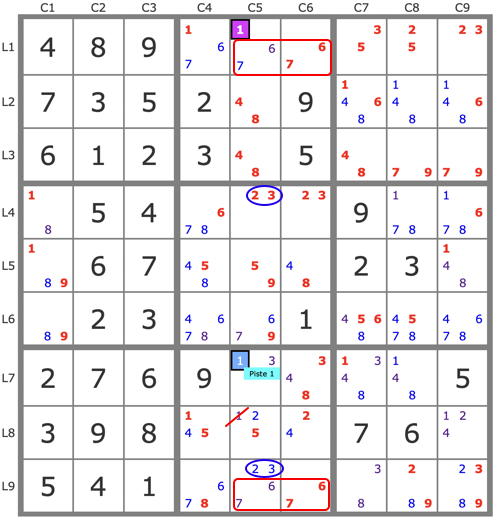
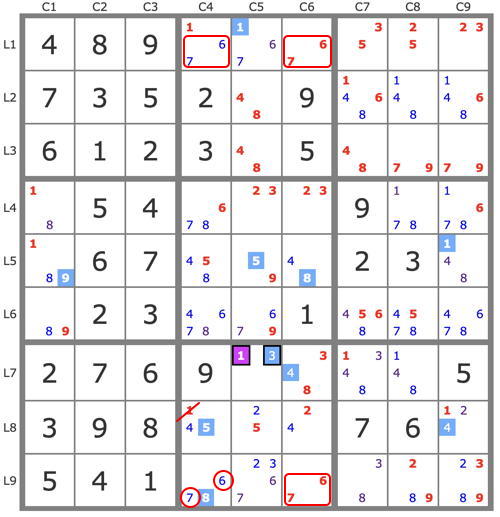
The best resolutions have been presented, notably the one from François (DEFISE). Here is one exploiting the two almost UR so visible!

UR(67r19c56) : (-1r1c5)->23r49c5->1r7c5->... => -1r8c5

puzzle1: Show

UR(67r19c46) : (-1r1c5)->(3r7c5->1r1c5->8r9c4)->4r7c6->[ (8r5c6 and 4r8c9)->1r5c9 ]->9r5c1->5r5c5->5r8c4->... => -1r8c4 => r7c5=1, stte

puzzle2: Show

Robert

[jco]

Hi Robert,

I understand your move 2 in the following way:

Code: Select all

.---------------------------------------------------------------.
| 4     8     9     |c*167 b(1)67 c*67    | 35      25    23    |
| 7     3     5     |  2     48     9     | 1468    148   1468  |
| 6     1     2     |  3     48     5     | 48      79    79    |
|-------------------+---------------------+---------------------|
| 18    5     4     |  678   23     23    | 9       178   1678  |
|i189   6     7     |  458  j59    f48    | 2       3    h148   |
| 89    2     3     |  4678  679    1     | 4568    4578  4678  |
|-------------------+---------------------+---------------------|
| 2     7     6     |  9    a13    e348   |f'1348 f'148   5     |
| 3     9     8     | l145  k25     24    | 7       6   g'124   |
| 5     4     1     |d*67(8) 2367  *67    | 38      289   2389  |
'---------------------------------------------------------------'

Code: Select all

                                                                     (4)r7c78 = (4)r8c9
                                   UR                             /                     \
(3^-1)r7c5 = (1)r1c5 - (1=67)r1c46 - (6|7 = 8)r9c4 - (3^8 = 4)r7c6 ------ (4=8^^)r5c6-- continues next line

----(4|8=1)r5c9 - (18^^ = 9)r5c1 - (9=5)r5c5 - (5)r8c5 = (5)r8c4

where ^, ^^ denote memory terms. I do not know the meaning of "(-1 r1c5)" at the start, but it seems that you considered the consequences of r7c5 = 3 and arrived at the conclusion that r8c4=5. As r7c5 is a BVC, you proved that either (1)r7c5 or (5)r8c4, i.e., -1 r8c4.
Why the dots at the end ?
Interesting that at first I could not follow your move from the placement of 9 at r5c1 because I had some placements after move 1 (see edit for the reason).

Regards,

Edit: The reason for the difference ("singles" after move 1) is that in move 1, using the UR, we can eliminate also 2 from r8c5.
Then r5c1 is left with only 18. You did not perform this additional elimination:

Code: Select all

.------------------------------------------------------------.
| 4     8     9     | 167 *(1)67  *67    | 35    25    23    |
| 7     3     5     | 2     48     9     | 1468  148   1468  |
| 6     1     2     | 3     48     5     | 48    79    79    |
|-------------------+--------------------+-------------------|
| 18    5     4     | 678  (23)    23    | 9     178   1678  |
| 189   6     7     | 458   59     48    | 2     3     148   |
| 89    2     3     | 4678  679    1     | 4568  4578  4678  |
|-------------------+--------------------+-------------------|
| 2     7     6     | 9    (13)    348   | 1348  148   5     |
| 3     9     8     | 145   5-12   24    | 7     6     124   |
| 5     4     1     | 678 *(23)67 *67    | 38    289   2389  |
'------------------------------------------------------------'

UR (67)r19c56 using internals => -2 r7c5 [only chains for this elimination shown]
(1)r1c5 - (1=32)r79c5
(2)r9c5
(3)r9c5 - (3=2)r4c5
=> -2 r9c5
Using both eliminations (in the same move 1), the second UR(67)r19c46 can be used as follows

Code: Select all

.-----------------------------------------------.
| 4   8  9 |a167   167   67  | 35    25    23   |
| 7   3  5 | 2     48    9   | 1468  148   1468 |
| 6   1  2 | 3     48    5   | 48    79    79   |
|----------+-----------------+------------------|
| 18  5  4 | 678  B23   C23  | 9     178   1678 |
|e18  6  7 | 5     9    d48  | 2     3    e148  |
| 9   2  3 | 4678  67    1   | 4568  4578  4678 |
|----------+-----------------+------------------|
| 2   7  6 | 9    A13   c348 | 1348  148   5    |
| 3   9  8 | 4-1   5    D24  | 7     6   fE14(2)|
| 5   4  1 |b678   2367  67  | 38    289   2389 |
'-----------------------------------------------'

(1=3)r7c5 - r4c5 = (3-2)r4c6 = (2)r8c6 - (2*)r8c9 = [(1)r1c4 =UR= (8)r9c4 - (8)r7c6 = (8)r5c6 - (8=14)r5c19 - (4*=*1)r8c9 ]
=> -1 r8c4
Edit 2: improved the text for clarity.

[Mauriès Robert]

Hi JCO,

I'm not sure I understand what you're explaining to me, just as I'm not sure you understand what I did with the almost UR.
So I will clarify what I have done.
1) First about the meaning of a sequence of the form (-A)->B->C->... which I call anti-track from A:
(-A) means that I examine what happens in the puzzle when I delete candidate A. The puzzle generated by this deletion makes appear new singles B, C etc and possibly closed sets. The ... means that I can continue the construction but that it is not necessary for the conclusion I am looking for :
If a candidate sees both A and one of the candidates of the sequence B, C, etc... this candidate can be eliminated.
2) In the case of the puzzle 32 with a unique solution, deleting A=1r1c5 makes it appear that in the generated puzzle the cell r9c5 necessarily contains 23 in order to have a unique solution and this makes the closed set 23r49c5 and consequently also the 1r7c5 appear as a single, so (-1r1c5)->23r9c5->1r7c5->... and this is enough to eliminate the 1r8C5 from the puzzle 32.
The same applies to the second step.
Robert

[jco]

Hi Robert,

The summary of my observation is that, it seems that making two eliminations in step1 allows a simpler chain in step 2, but of course the net effect is the same as your proposed solution. Thanks for the explanation.